发表更新密码学 / 古典密码2 小时读完 (大约14613个字)  次访问

[古典密码] 单表替换密码

序言

假设你正置身 16 世纪的大航海时代，商队凭借英法两国间的羊毛贸易往来日进斗金。信使的船帆在英吉利海峡上来回穿梭，帆布上的家族纹章曾是你最引以为傲的标志 —— 直到阴影悄然笼罩。最近三封关于羊毛贸易的明文信件都被竞争对手破译，导致两次货运路线被抢，损失惨重。你深知，再用明文传递信息，无异于将商业机密拱手让人。

这日，你坐在伦敦商会的橡木桌前，指尖划过一封刚写好的信：“下月初三，携佛兰德斯羊毛至多佛港，与约克公爵代理人交接，暗号‘红玫瑰’。” 窗外细雨绵绵，你却额头冒汗 —— 这封信若再被截获，不仅血本无归，恐怕还要背上“私通贵族”的罪名。

“必须让他们看不懂。”你咬着笔杆，目光扫过桌上的杂物：账本、印章、还有一卷上周从威尼斯商人手里换来的羊皮纸。你随手把它扯过来，展开时，朱砂画的字符在烛光下格外清晰 —— 是一列 A 到 Z 的拉丁字母。

“一个字母表？能做什么？”你眉头微蹙，该如何设计加密方式，让窥探者无计可施？雨还在下，敲得窗棂咚咚作响，像在催促一个答案。羊皮纸上的朱砂字母在烛光里明明灭灭，仿佛在等你给它们重新编排命运……

其实很容易想到用字母表中的其他字母替换信件中的明文，为每个字母寻找“替身”，A 替换成 M、B 替换成 N。使明文变成毫无意义的字符串。单表替换密码（Monoalphabetic Substitution Cipher）正是这样一种经典的加密方式，其核心在于：每个字母始终被替换为另一个唯一的字母，整个过程基于一个固定的替换表。由于替换是一一对应的，知道替换表就能轻松还原原文。接下来让我们使用单表替换密码对机密信件进行加密。


1. ROT 密码

既然是替换，就得有个确定的规则，不能随意替换，否则除你之外谁也看不懂，加密也就失去了意义。在罗马共和时期，尤利乌斯・凯撒（Julius Caesar）为保障军事信件的安全，想出了一套加密规则，以此与前线作战的将军们传递信息，防止被敌军截获后破译。他规定，明文中的所有字母都需在字母表上向后偏移 3 位，以此生成密文：A 替换为 D，B 替换为 E，依此类推；到了字母表末尾则循环衔接，X 变为 A，Y 变为 B，Z 变为 C。经此处理，原本表意清晰的明文便转化为外人难以解读的密文。

随着历史的推进，基于不同偏移量的单表替换密码陆续出现 —— 比如偏移量为 5 的 ROT5、偏移量为 13 的 ROT13 等。这类依靠固定偏移进行替换的规则，操作简单且易于推行。以如今的眼光看，它们的破解难度极低；但在当时，受限于技术条件，这种最基础、最简单的替换密码，曾是许多人难以攻克的信息屏障。

后世人们对这类基于固定偏移的单表替换密码加以系统整理，最终归纳出了 ROT 密码体系。ROT 密码（Rotate Cipher）是一种最经典的单表替换加密算法，将明文中的每个字母在字母表中按固定的偏移量向前或向后移动来加密文本。偏移量默认为正，表示向后（右）移动；偏移量为负，表示向前（左）移动。

按种类大致分为：ROT5、Caesar Cipher、ROT13、ROT18、ROT47

1.1 ROT5

1.1.1 加解密原理

ROT5（rotate by 5 places）是一种只针对数字的编码方式，采用对 0–9 的循环偏移。每个数字向后移动 5 位，例如 0 编码为 5，1 编码为 6，以此类推，超过 9 后从 0 重新开始，形成一个 10 进制的循环替换。其他字符均保持不变。该加密方式具有自反性，即加密两次即可还原原文。

1
2
明文数字表：0123456789
密文数字表：5678901234

代码实现（python）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class ROT5Cipher:
    """ROT5密码加解密"""
    
    @staticmethod
    def _shift_char(char, shift):
        """对单个字符进行移位处理，非数字字符保持不变"""
        if char.isdigit():
            return str((int(char) + shift) % 10)
        return char
    
    @classmethod
    def encrypt(cls, plaintext):
        """加密：数字字符加5取模10，其他字符不变"""
        return ''.join([cls._shift_char(c, 5) for c in plaintext])
    
    @classmethod
    def decrypt(cls, ciphertext):
        """解密：数字字符减5取模10，其他字符不变"""
        return ''.join([cls._shift_char(c, -5) for c in ciphertext])


if __name__ == "__main__":
    original = "Hello, I am DSTBP! 123 456"
    encrypted = ROT5Cipher.encrypt(original)
    decrypted = ROT5Cipher.decrypt(encrypted)
    
    print(f"原始文本: {original}\n加密后: {encrypted}\n解密后: {decrypted}")

    '''
    原始文本: Hello, I am DSTBP! 123 456
    加密后: Hello, I am DSTBP! 678 901
    解密后: Hello, I am DSTBP! 123 456
    '''

1.2 ROT13

1.2.1 加解密原理

ROT13 只对字母进行加密。其偏移量为 13，例如 A 编码为 N，B 编码为 O，依此类推，超过范围后从头开始。非字母字符保持不变，且该加密方式也具有自反性。

1
2
明文字母表：ABCDEFGHIJKLMNOPQRSTUVWXYZ abcdefghijklmnopqrstuvwxyz
密文字母表：NOPQRSTUVWXYZABCDEFGHIJKLM nopqrstuvwxyzabcdefghijklm

代码实现（python）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class ROT13Cipher:
    """ROT13密码加解密"""
    
    @staticmethod
    def _shift_char(char: str) -> str:
        """对单个字符进行ROT13移位，非字母字符保持不变"""
        if not char.isalpha():
            return char
            
        # 确定字母的基准ASCII值（大写65，小写97）
        base = ord('A') if char.isupper() else ord('a')
        # 计算移位后的值（加13和减13效果相同，因为26%13=0）
        shifted = (ord(char) - base + 13) % 26
        return chr(shifted + base)
    
    @classmethod
    def transform(cls, text: str) -> str:
        """加密和解密统一方法（ROT13加密解密相同）"""
        return ''.join(cls._shift_char(c) for c in text)
    
    # 保持接口一致性
    encrypt = transform
    decrypt = transform


if __name__ == "__main__":
    original = "Hello, I am DSTBP! 123 456"
    encrypted = ROT13Cipher.encrypt(original)
    decrypted = ROT13Cipher.decrypt(encrypted)
    
    print(f"原始文本: {original}")
    print(f"加密后: {encrypted}")
    print(f"解密后: {decrypted}")

    '''
    原始文本: Hello, I am DSTBP! 123 456
    加密后: Uryyb, V nz QFGOC! 123 456
    解密后: Hello, I am DSTBP! 123 456
    '''

1.3 凯撒密码

1.3.1 加解密原理

Caesar Cipher（凯撒密码）也是一种对字母进行加密的单表替换方法。它将每个字母在 A–Z 或 a–z 范围内循环向后偏移 3 位，非字母字符保持原样。解密时，只需将字母向前偏移 3 位即可还原原文。

1
2
明文字母表：ABCDEFGHIJKLMNOPQRSTUVWXYZ
密文字母表：DEFGHIJKLMNOPQRSTUVWXYZABC

代码实现（python）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class CaesarCipher:
    """
    凯撒密码加解密类
    """
    @staticmethod
    def _shift_char(char: str, offest: int) -> str:
        """对单个字符进行指定偏移量的移位，非字母字符保持不变"""
        if not char.isalpha():
            return char
            
        # 确定字母的基准ASCII值（大写65，小写97）
        base = ord('A') if char.isupper() else ord('a')
        shifted = (ord(char) - base + offest) % 26
        return chr(shifted + base)
    
    @classmethod
    def encrypt(cls, text: str) -> str:
        """对文本进行加密"""
        return ''.join(cls._shift_char(c, 3) for c in text)
    
    @classmethod
    def decrypt(cls, text: str) -> str:
        """对文本进行解密"""
        return ''.join(cls._shift_char(c, -3) for c in text)


if __name__ == "__main__":
    original = "Hello, I am DSTBP! 123 456"
    encrypted = CaesarCipher.encrypt(original)
    decrypted = CaesarCipher.decrypt(encrypted)
    
    print(f"原始文本: {original}")
    print(f"加密后: {encrypted}")
    print(f"解密后: {decrypted}")

    '''
    原始文本: Hello, I am DSTBP! 123 456
    加密后: Khoor, L dp GVWES! 123 456
    解密后: Hello, I am DSTBP! 123 456
    '''

1.4 ROT18

1.4.1 加解密原理

ROT18 其实是非标准加密，原本并不存在这一命名，仅为便于称呼而将这种组合称为 ROT18。它结合了 ROT13 和 ROT5：对字母执行 ROT13，对数字执行 ROT5。

代码实现（python）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class ROT18Cipher:
    """ROT18密码加解密"""
    
    @staticmethod
    def _shift_char(char):
        """对单个字符进行ROT18处理：字母用ROT13，数字用ROT5，其他字符不变"""
        if char.isalpha():
            # 字母应用ROT13变换
            base = ord('A') if char.isupper() else ord('a')
            shifted = (ord(char) - base + 13) % 26
            return chr(shifted + base)
        elif char.isdigit():
            # 数字应用ROT5变换
            return str((int(char) + 5) % 10)
        # 非字母数字字符保持不变
        return char
    
    @classmethod
    def encrypt(cls, plaintext):
        """加密：对字母执行 ROT13，对数字执行 ROT5，其他字符不变"""
        return ''.join([cls._shift_char(c) for c in plaintext])
    
    @classmethod
    def decrypt(cls, ciphertext):
        """解密：ROT18加密解密相同，执行相同操作即可还原"""
        return ''.join([cls._shift_char(c) for c in ciphertext])


if __name__ == "__main__":
    original = "Hello, I am DSTBP! 123 456"
    encrypted = ROT18Cipher.encrypt(original)
    decrypted = ROT18Cipher.decrypt(encrypted)
    
    print(f"原始文本: {original}")
    print(f"加密后: {encrypted}")
    print(f"解密后: {decrypted}")

    '''
    原始文本: Hello, I am DSTBP! 123 456
    加密后: Uryyb, V nz QFGOC! 678 901
    解密后: Hello, I am DSTBP! 123 456
    '''

1.5 ROT47

1.5.1 加解密原理

引入 ASCII 码，对数字、字母、常用符号进行加密，字符范围限定在 33 到 126 之间，并使用固定步长 47 进行替换。加密时，以当前字符的 ASCII 值为起点，向后数第 47 个位置所对应的字符替换当前字符。例如，小写字母 z 编码后变为大写 K，数字 0 编码后变为符号 _。

1
2
明文字母表：!"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstuvwxyz{|}~
密文字母表：PQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstuvwxyz{|}~!"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNO

代码实现（python）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class ROT47Cipher:
    """ROT47密码加解密"""
    
    @staticmethod
    def _shift_char(char):
        """对单个字符进行ROT47处理：可打印字符移位47，其他字符不变"""
        ord_char = ord(char)
        if 33 <= ord_char <= 126:
            # 移位公式：(原位置 - 33 + 47) % 94 + 33（94为可打印字符总数）
            shifted_ord = (ord_char - 33 + 47) % 94 + 33
            return chr(shifted_ord)
        # 非可打印字符保持不变
        return char
    
    @classmethod
    def encrypt(cls, plaintext):
        """加密：对可打印字符执行ROT47移位，其他字符不变"""
        return ''.join([cls._shift_char(c) for c in plaintext])
    
    @classmethod
    def decrypt(cls, ciphertext):
        """解密：ROT47加密解密相同，执行相同操作即可还原"""
        return ''.join([cls._shift_char(c) for c in ciphertext])


# 使用示例
if __name__ == "__main__":
    original = "Hello, I am DSTBP! 123 456"

    encrypted = ROT47Cipher.encrypt(original)
    decrypted = ROT47Cipher.decrypt(encrypted)
    
    print(f"原始文本: {original}")
    print(f"加密后: {encrypted}")
    print(f"解密后: {decrypted}")

    '''
    原始文本: Hello, I am DSTBP! 123 456
    加密后: w6==@[ x 2> s$%q!P `ab cde
    解密后: Hello, I am DSTBP! 123 456
    '''

1.6 广义 ROT 密码

1.6.1 加解密原理

除了上面提到的常见偏移量算法之外，还有一些使用非常见偏移量的加密方式，例如 Avocat（偏移量为 10）、Cassis（偏移量为 -5）、Cassette（偏移量为 -6）。由此可以看出，偏移量本质上就是 ROT13 等加密算法的密钥，不同的偏移值会产生完全不同的密文。

下面给出自定义偏移量的广义 ROT 密码的代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
class GeneralizedROTCipher:
    """广义ROT密码加解密"""
    @staticmethod
    def _shift_char(char, alphabet, offset):
        """对单个字符进行移位处理：码表内字符按偏移量移位，其他字符不变"""
        if char in alphabet:
            # 计算移位后在码表中的位置
            char_index = alphabet.index(char)
            shifted_index = (char_index + offset) % len(alphabet)
            return alphabet[shifted_index]
        return char  # 不在码表中的字符保持不变
    
    @staticmethod
    def _is_case_mixed(alphabet):
        """判断码表是否大小写混用"""
        has_upper = any(c.isupper() for c in alphabet)
        has_lower = any(c.islower() for c in alphabet)
        return has_upper and has_lower
    
    @staticmethod
    def _normalize_case(text, alphabet):
        """根据码表类型标准化文本大小写"""
        if GeneralizedROTCipher._is_case_mixed(alphabet):
            return text  # 码表大小写混用，保持原样
        
        # 判断码表类型
        is_upper_alphabet = alphabet[0].isupper() if alphabet else False
        
        normalized = ""
        for char in text:
            if char.isalpha():
                if is_upper_alphabet:
                    normalized += char.upper()
                else:
                    normalized += char.lower()
            else:
                normalized += char
        
        return normalized
    
    @staticmethod
    def _restore_case(processed_text, original_text):
        """恢复原始文本的大小写"""
        result = ""
        for i, char in enumerate(processed_text):
            if i < len(original_text) and char.isalpha() and original_text[i].isalpha():
                # 恢复原始大小写
                if original_text[i].isupper():
                    result += char.upper()
                else:
                    result += char.lower()
            else:
                result += char
        return result
    
    @classmethod
    def encrypt(cls, plaintext, offset, alphabet='abcdefghijklmnopqrstuvwxyz', case_sensitive=True):
        """加密：对码表内字符按指定偏移量移位"""
        if len(set(alphabet)) != len(alphabet):
            raise ValueError("码表中存在重复字符")
        
        if case_sensitive:
            # 大小写敏感模式，直接处理
            return ''.join([cls._shift_char(c, alphabet, offset) for c in plaintext])
        else:
            # 大小写不敏感模式
            # 1. 判断码表是否大小写混用
            if cls._is_case_mixed(alphabet):
                # 码表大小写混用，直接处理
                return ''.join([cls._shift_char(c, alphabet, offset) for c in plaintext])
            else:
                # 码表不混用，按码表类型标准化处理
                normalized_text = cls._normalize_case(plaintext, alphabet)
                processed_text = ''.join([cls._shift_char(c, alphabet, offset) for c in normalized_text])
                # 恢复原始大小写
                return cls._restore_case(processed_text, plaintext)
    
    @classmethod
    def decrypt(cls, ciphertext, offset, alphabet='abcdefghijklmnopqrstuvwxyz', case_sensitive=True):
        """解密：对码表内字符按负偏移量移位（逆向操作）"""
        if len(set(alphabet)) != len(alphabet):
            raise ValueError("码表中存在重复字符")
        
        if case_sensitive:
            # 大小写敏感模式，直接处理
            return ''.join([cls._shift_char(c, alphabet, -offset) for c in ciphertext])
        else:
            # 大小写不敏感模式
            # 1. 判断码表是否大小写混用
            if cls._is_case_mixed(alphabet):
                # 码表大小写混用，直接处理
                return ''.join([cls._shift_char(c, alphabet, -offset) for c in ciphertext])
            else:
                # 码表不混用，按码表类型标准化处理
                normalized_text = cls._normalize_case(ciphertext, alphabet)
                processed_text = ''.join([cls._shift_char(c, alphabet, -offset) for c in normalized_text])
                # 恢复原始大小写
                return cls._restore_case(processed_text, ciphertext)


if __name__ == "__main__":
    original = "Hello, I am Dstbp! 123 456"

    encrypted = GeneralizedROTCipher.encrypt(original, 5, case_sensitive=False)
    decrypted = GeneralizedROTCipher.decrypt(encrypted, 5, case_sensitive=False)
    print(f"原始文本: {original}")
    print(f"加密后: {encrypted}")
    print(f"解密后: {decrypted}")
    print()

    '''
    原始文本: Hello, I am Dstbp! 123 456
    加密后: Mjqqt, N fr Ixygu! 123 456
    解密后: Hello, I am Dstbp! 123 456
    '''

1.6.2 攻击手段

唯密文攻击

由于使用 ROT 加密的语言通常基于字母文字系统，偏移量的范围是有限的。例如在使用 26 个字母的英文中，最大有效偏移量为 25，偏移量超过 26 会循环回到 1–25 的范围。因此，如果偏移量未知，可以通过穷举所有可能值轻松破解，加密强度较低。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
def brute_force_rot(ciphertext: str, alphabet: str) -> dict:
    """
    爆破已知码表下的未知偏移量
    """
    if not alphabet:
        raise ValueError("码表不能为空")
    if len(set(alphabet)) != len(alphabet):
        raise ValueError("码表中存在重复字符")
    
    max_offset = len(alphabet)
    results = {}
    
    # 爆破所有可能的偏移量（0到max_offset-1）
    for offset in range(max_offset):
        plaintext = []
        for char in ciphertext:
            if char in alphabet:
                char_idx = alphabet.index(char)
                decrypted_idx = (char_idx - offset) % max_offset
                plaintext.append(alphabet[decrypted_idx])
            else:
                # 非码表字符直接保留
                plaintext.append(char)
        results[offset] = ''.join(plaintext)
    
    return results



if __name__ == "__main__":
    known_alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz"
    ciphertext = "CZggj, D Vh yNOwK! 123 456"
    
    # 爆破所有可能的偏移量
    decrypted_results = brute_force_rot(ciphertext, known_alphabet)

    for offset, text in decrypted_results.items():
        print(f"偏移量 {offset:2d}: {text}")

    # 偏移量 47: Hello, I am DSTBP! 123 456

1.6.3 方法改进

ROT 密码的偏移量选择有限，极易被穷举破解，若用它来加密我们的贸易信件，安全性自然无从谈起。那么，有没有办法改进传统的 ROT 加密，提升其抗破解能力呢？

ROT 加密的核心在于两个要素：偏移量和码表。要增强其安全性，可以尝试从这两方面进行改进。

自变偏移 ROT 密码（Self-changing Offset ROT Cipher）

从偏移量来看，常规 ROT 加密采用的是固定偏移，即每个字母都按照相同的数值偏移，加密模式过于单一。为了提升复杂度，可以引入动态偏移机制：从一个初始偏移量开始，每加密一个字符，偏移量递增 1，从而实现偏移量逐字符变化的加密效果。

代码实现（python）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
class SelfChangingOffsetROT:
    """
    支持自定义码表的自变偏移 ROT 密码
    """
    @staticmethod
    def _shift_char(char: str, offset: int, alphabet: str) -> str:
        """根据自定义码表和偏移量处理单个字符"""
        if char not in alphabet:
            return char  # 不在码表中的字符直接保留
            
        # 计算移位后在码表中的位置
        char_index = alphabet.index(char)
        shifted_index = (char_index + offset) % len(alphabet)
        return alphabet[shifted_index]
    
    @classmethod
    def encrypt(cls, plaintext: str, initial_offset: int, alphabet: str='ABCDEFGHIJKLMNOPQRSTUVWXYZ') -> str:
        """加密：使用自定义码表，偏移量从初始值开始逐字符递增"""
        if len(set(alphabet)) != len(alphabet):
            raise ValueError("码表中存在重复字符")
        ciphertext = []
        current_offset = initial_offset
        
        for char in plaintext:
            # 对当前字符进行移位
            cipher_char = cls._shift_char(char, current_offset, alphabet)
            ciphertext.append(cipher_char)
            # 仅对码表中的字符递增偏移量
            if char in alphabet:
                current_offset += 1
                
        return ''.join(ciphertext)
    
    @classmethod
    def decrypt(cls, ciphertext: str, initial_offset: int, alphabet: str='ABCDEFGHIJKLMNOPQRSTUVWXYZ') -> str:
        """解密：使用自定义码表，偏移量规则与加密一致"""
        if len(set(alphabet)) != len(alphabet):
            raise ValueError("码表中存在重复字符")
        plaintext = []
        current_offset = initial_offset
        
        for char in ciphertext:
            # 解密使用负偏移量
            plain_char = cls._shift_char(char, -current_offset, alphabet)
            plaintext.append(plain_char)
            # 仅对码表中的字符递增偏移量
            if char in alphabet:
                current_offset += 1
                
        return ''.join(plaintext)


if __name__ == "__main__":
    original = "Hello, I am DSTBP! 123 456"
    initial_offset = 14
    custom_alphabet = "0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstuvwxyz{|}~"
    
    encrypted = SelfChangingOffsetROT.encrypt(original, initial_offset, custom_alphabet)
    decrypted = SelfChangingOffsetROT.decrypt(encrypted, initial_offset, custom_alphabet)
    print(f"原始文本: {original}")
    print(f"加密后: {encrypted}")
    print(f"解密后: {decrypted}")

    '''
    原始文本: Hello, I am DSTBP! 123 456
    加密后: Vt|}2, \ u3 Zjl[j! LNP RTV
    解密后: Hello, I am DSTBP! 123 456
    '''

基于密钥的 ROT 密码（Keyed ROT Cipher，也称 Keyed Casear Cipher）

再看码表，标准 ROT 密码始终基于固定顺序的字母表 —— 无论偏移量如何，字母之间的相对位置保持不变（如 A 后总是 B，B 后总是 C）。为打破这一规律，可以基于密钥构造一个自定义字母表。方法是：先提取密钥中的字母，按出现顺序去重排列，再将未出现的字母按字母顺序补全。例如，若密钥为 “cryptotion”，生成的字母表为 CRYPTOINABDEFGHJKLMQSUVWXZ。加密时用该字母表替代标准字母表，结合偏移实现替换操作，其余逻辑与凯撒加密一致。

代码实现（python）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
class KeyedCaesarCipher:
    """
    带密钥的凯撒密码加解密类
    """
    @staticmethod
    def _build_alphabet(key: str) -> str:
        """
        根据密钥构建加密字母表
        """
        # 提取密钥中唯一字母（大写）
        key_chars = [c.upper() for c in key if c.isalpha()]
        unique_key = []
        for c in key_chars:
            if c not in unique_key:
                unique_key.append(c)
        
        # 补充剩余字母（排除已在密钥中出现的）
        all_letters = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
        remaining = [c for c in all_letters if c not in unique_key]
        
        return ''.join(unique_key + remaining)
    
    @classmethod
    def encrypt(cls, plaintext: str, key: str, offset: int) -> str:
        """
        加密：使用密钥字母表和偏移量
        """
        ciphertext = []
        base_alphabet = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
        key_alphabet = cls._build_alphabet(key)
        offset = offset % 26  # 确保偏移量在0-25之间
        
        for char in plaintext:
            if not char.isalpha():
                # 非字母字符直接保留
                ciphertext.append(char)
                continue
                
            # 找到在基础字母表中的位置
            idx = base_alphabet.index(char.upper())
            # 计算加密后在密钥字母表中的位置
            encrypted_idx = (idx + offset) % 26
            encrypted_char = key_alphabet[encrypted_idx]
            
            # 恢复原始大小写
            ciphertext.append(encrypted_char if char.isupper() else encrypted_char.lower())
            
        return ''.join(ciphertext)
    
    @classmethod
    def decrypt(cls, ciphertext: str, key: str, offset: int) -> str:
        """
        解密：使用密钥字母表和偏移量
        """
        plaintext = []
        base_alphabet = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
        key_alphabet = cls._build_alphabet(key)
        offset = offset % 26  # 确保偏移量在0-25之间
        
        for char in ciphertext:
            if not char.isalpha():
                # 非字母字符直接保留
                plaintext.append(char)
                continue
                
            is_upper = char.isupper()
            char_upper = char.upper()
            # 找到在密钥字母表中的位置
            idx = key_alphabet.index(char_upper)
            # 计算解密后在基础字母表中的位置
            decrypted_idx = (idx - offset) % 26
            decrypted_char = base_alphabet[decrypted_idx]
            
            # 恢复原始大小写
            plaintext.append(decrypted_char if is_upper else decrypted_char.lower())
            
        return ''.join(plaintext)


if __name__ == "__main__":
    key = "cryptotion"
    offset = 2
    
    # 加密示例
    original = "Hello, I am DSTBP! 123 456"
    encrypted = KeyedCaesarCipher.encrypt(original, key, offset)
    print(f"原始文本: {original}")
    print(f"加密后: {encrypted}")
    
    # 解密示例
    decrypted = KeyedCaesarCipher.decrypt(encrypted, key, offset)
    print(f"解密后: {decrypted}")

    '''
    原始文本: Hello, I am DSTBP! 123 456
    加密后: Biggk, D yh OSUPL! 123 456
    解密后: Hello, I am DSTBP! 123 456
    '''

2. Atbash Cipher

自变偏移的 ROT 加密在一定程度上提高了爆破难度（初始偏移 × 增加步长，共 26 × 26 种组合），但总量仍有限，依然容易被暴力破解。而基于密钥的凯撒密码虽然通过打乱码表顺序提升了安全性，但由于密钥通常较短，能覆盖的字母种类有限，其余未出现的字母仍按标准顺序补全，整体码表的变化空间依然受限。

那么，有没有更彻底的方式来打破字母表的固定顺序，重新编排码表呢？比如将整个字母表完全反转。如果你产生了这种想法，那么恭喜你，你就和公元 1 世纪的萨多吉等教派信徒对上脑电波了。

2.1 加解密原理

Atbash Cipher（埃特巴什码）也是一种单表替换密码，这种密码曾被公元 1 世纪的艾赛尼、萨多吉教派的经文中，用以隐藏姓名。由熊斐特博士（Dr. Robert Eisenman）发现，他使用这种加密方法来解读艾赛尼、萨多吉教派的经文。其加密规则是将字母表反转：第一个字母对应最后一个，第二个对应倒数第二个。

1
2
明文字母表：ABCDEFGHIJKLMNOPQRSTUVWXYZ
密文字母表：ZYXWVUTSRQPONMLKJIHGFEDCBA

代码实现（python）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class AtbashCipher:
    """Atbash Cipher 埃特巴什码"""
    @staticmethod
    def _shift_char(char):
        """对单个字符进行移位处理"""
        if not char.isalpha():
            return char
        
        base = ord('A') if char.isupper() else ord('a')
        shifted_index = -ord(char) + base + 25
        return chr(base + shifted_index)
    
    @classmethod
    def encrypt(cls, plaintext):
        """加密"""
        return ''.join([cls._shift_char(c) for c in plaintext])
    
    @classmethod
    def decrypt(cls, ciphertext):
        """解密"""
        return ''.join([cls._shift_char(c) for c in ciphertext])


if __name__ == "__main__":
    original = 'Hello, I am DSTBP! 123 456'

    encrypted = AtbashCipher.encrypt(original)
    decrypted = AtbashCipher.decrypt(encrypted)

    print(f"原始文本: {original}")
    print(f"加密后: {encrypted}")
    print(f"解密后: {decrypted}")

    '''
    原始文本: Hello, I am DSTBP! 123 456
    加密后: Svool, R zn WHGYK! 123 456
    解密后: Hello, I am DSTBP! 123 456
    '''

2.2 扩展埃特巴什码

标准的 Atbash Cipher 只是对 26 个字母表进行一次简单反转，对于有经验的分析者来说相当容易破解。但这种思路可以拓展：在反转的基础上，将字母表划分为若干段，并对这些段之间的顺序进行重新排列。例如：

1
2
3
4
5
明文字母表：                      ABCDEFGHIJKLMNOPQRSTUVWXYZ
标准 Atbash Cipher 密文字母表：   ZYXWVUTSRQPONMLKJIHGFEDCBA
划分三段：       			   ZYXWVUT SRQPONMLK JIHGFEDCBA
交换顺序是 312：                 JIHGFEDCBA ZYXWVUT SRQPONMLK
最终变种密文字母表：              JIHGFEDCBAZYXWVUTSRQPONMLK

段的长度和交换顺序可作为加密密钥，使加密过程更加灵活可控，从而显著提高加密的复杂度与破解难度。

代码实现（python）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
class ExtendAtbashCipher:
    """
    Extend Atbash Cipher 扩展埃特巴什码
    """
    def __init__(self, key: str):
        """构建明文密文对应码表"""
        self.key = self._build_alphabet(key)

    def _build_alphabet(self, key: str):
        key_list = key.split(" ")
        index_list = list(map(int, key_list[:-1]))
        order_list = list(map(int, key_list[-1]))

        # 合法性校验
        if sum(index_list) != 26 and len(key_list[:-1]) != len(key_list[-1]):
            raise ValueError("密钥有误")
        
        # 切片
        ua = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
        segments = []
        start = 0
        for length in index_list:
            end = start + length
            segments.append(ua[::-1][start:end])
            start = end

        # 调整顺序
        res = ''.join(segments[i-1] for i in order_list)
        return dict(zip(ua, res))

    def _shift_char(self, char: str, key: dict):
        """对单个字符进行操作"""
        if not char.isalpha():
            return char
        if char.isupper():
            return key[char]
        else:
            return key[char.upper()].lower()

    def encrypt(self, plaintext: str):
        """加密"""
        return ''.join([self._shift_char(c, self.key) for c in plaintext])

    def decrypt(self, ciphertext: str):
        """解密"""
        key = dict(zip(self.key.values(), self.key.keys()))
        return ''.join([self._shift_char(c, key) for c in ciphertext])


if __name__ == "__main__":
    original = 'Hello, I am DSTBP! 123 456'
    key = "7 9 10 312"

    eac = ExtendAtbashCipher(key)

    encrypted = eac.encrypt(original)
    decrypted = eac.decrypt(encrypted)

    print(f"原始文本: {original}")
    print(f"加密后: {encrypted}")
    print(f"解密后: {decrypted}")

    '''
    原始文本: Hello, I am DSTBP! 123 456
    加密后: Cfyyv, B jx GRQIU! 123 456
    解密后: Hello, I am DSTBP! 123 456
    '''

3. 简单替换密码

3.1 加解密原理

可以看出，扩展后的 Atbash 密码相比标准版本，其破解难度大大提升。攻击者不仅需要知道如何分段，还必须掌握各段的交换顺序。最复杂的情况是：每个字母被视为一个独立段，再根据密钥进行任意排列。敌手若不知排列顺序，穷举需尝试 $ 26! $ 种情况，也就是密钥空间为 $ 26! $，在有限时间内几乎无法爆破。

密码学中，这种通过对标准字母表进行任意排列（permutation）来构造密文映射的单表替换方式，被称为简单替换密码（Simple Substitution Cipher）。其中“简单”指的是结构简单：每个明文字母始终对应唯一的密文字母，加密过程依赖一个固定的替换表。区分于多表替换密码或更复杂的机械加密系统（详情请阅读 [古典密码] 多表替换密码）。

代码实现（python）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class SimpleSubCipher:
    """
    简单替换密码
    """
    def __init__(self, key: str):
        """构建明文密文对应码表"""
        self.key = self._build_alphabet(key)

    def _build_alphabet(self, key: str):
        upper_alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
        return dict(zip(upper_alpha, key.upper()))

    def _shift_char(self, char: str, key: dict):
        """对单个字符进行操作"""
        if not char.isalpha():
            return char
        if char.isupper():
            return key[char]
        else:
            return key[char.upper()].lower()

    def encrypt(self, plaintext: str):
        """加密"""
        return ''.join([self._shift_char(c, self.key) for c in plaintext])

    def decrypt(self, ciphertext: str):
        """解密"""
        key = dict(zip(self.key.values(), self.key.keys()))
        return ''.join([self._shift_char(c, key) for c in ciphertext])


if __name__ == "__main__":
    original = 'Hello, I am DSTBP! 123 456'
    key = "phqgiumeaylnofdxjkrcvstzwb"

    eac = SimpleSubCipher(key)

    encrypted = eac.encrypt(original)
    decrypted = eac.decrypt(encrypted)

    print(f"原始文本: {original}")
    print(f"加密后: {encrypted}")
    print(f"解密后: {decrypted}")

    '''
    原始文本: Hello, I am DSTBP! 123 456
    加密后: Einnd, A po GRCHX! 123 456
    解密后: Hello, I am DSTBP! 123 456
    '''

4. 仿射密码

前面介绍的 ROT 密码体系、Atbash 密码，虽各有其特点，但逐一记忆未免繁杂。这些加密方式的本质，都是通过简单的字母映射实现替换。那么，是否存在一种“大一统”的算法能够将它们整合，从数学角度用一个算式来概括这些密码呢？我们不妨自己先来推导一番。

首先是 ROT 密码体系，它的核心原理很直观：对字母表进行循环偏移。所谓“偏移”，即对字母的索引值进行加减偏移量的操作；而“循环”特性，则可通过取模运算来实现。这样，ROT 密码就可以概括为：

$$
E(x)=(x+b) \mod m
$$
$ b $ 为 3，表示凯撒密码，$ b $ 为 13，表示 ROT13，以此类推。

再分析 Atbash 密码，其将字母表进行反转，这个关系可写为：

$$
E(x)=(-x+25) \mod {26}
$$
由此可见，无论是 ROT 系列的“偏移”（加法），还是 Atbash 的“反转”（乘法），都可纳入同一框架。若用 $ a $ 表示线性变换的系数（控制缩放或反转），$ b $ 控制偏移量，$ m $ 表示模数（对 26 个字母而言 $ m=26 $），则所有这类单表替换密码都可统一表述为：

$$
E(x)=(ax+b) \mod m
$$
这便是仿射密码。

4.1 加解密原理

仿射密码（Affine Cipher）为单表加密的一种，字母系统中所有字母都基于一简单数学方程加密：
$$
E(x)=(ax+b) \mod m
$$
根据加密函数可以推导出解密方程：

$$
D(x)=a^{-1}(x-b) \mod m
$$
从解密函数可见，仿射密码若要实际应用（即确保能够解密），需满足一个前提：参数 $ a $ 在模 $m$ 的情况下有逆元。即 $ a、m $ 互质（$ \gcd(a,,m)=1 $）。

这里必须要求参数 $ a $ 存在模 26 的逆元，原因在于它控制的是字母表的缩放比例。

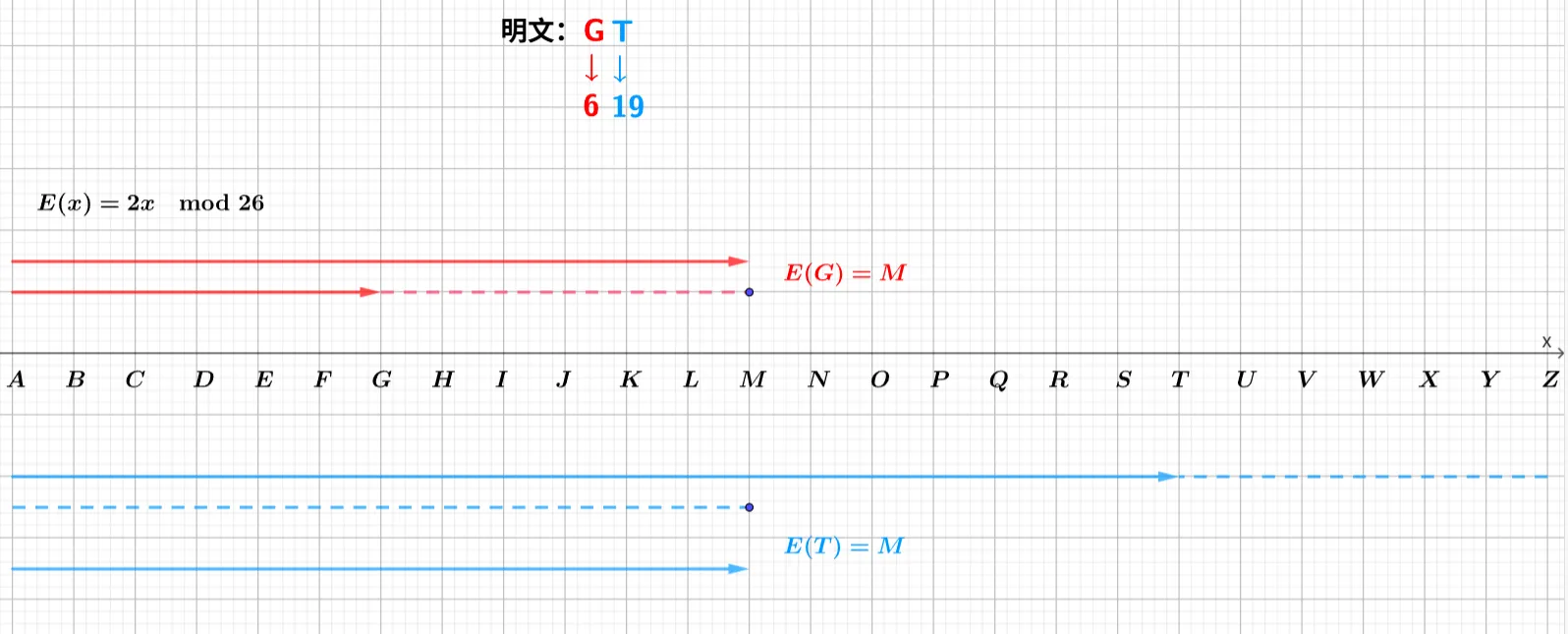
仿射密码基于仿射变换。可以将字母表视为一个数轴，字母 A 作为原点，每个明文字母的索引就像是从原点出发的一个向量。参数 $ a $ 就是对这个向量进行缩放的倍数，即将字母与原点之间的距离放大或缩小 $ a $ 倍。

图 4.1 参数 a 表示线性缩放

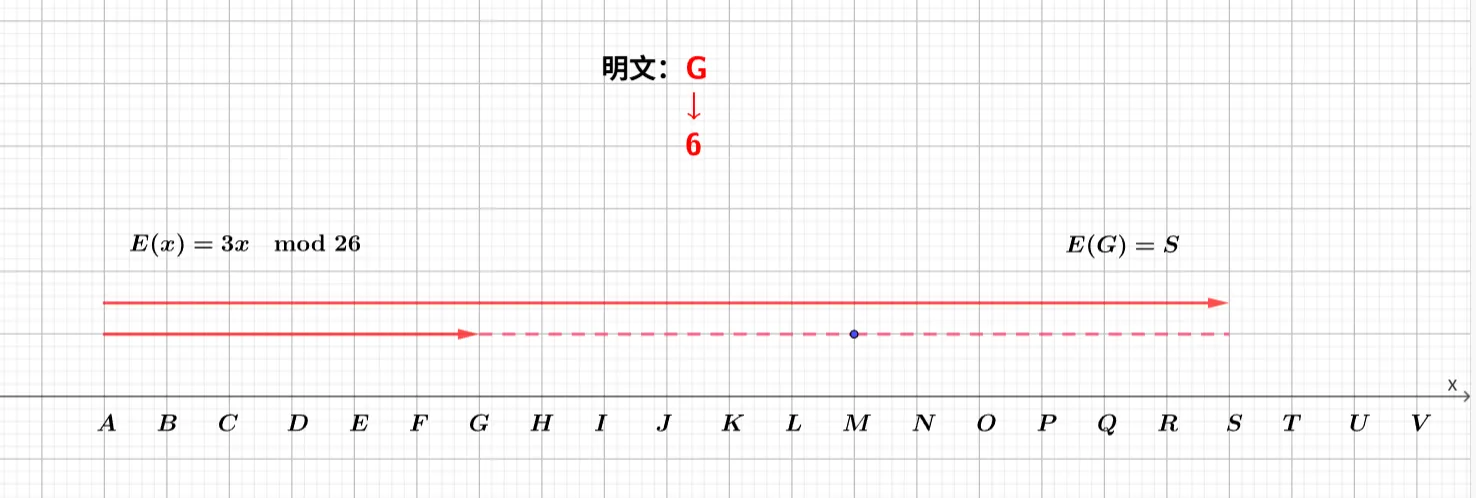
当缩放后的结果超出字母表范围时，通过取模运算将其折回范围内。但只有当 $ a $ 与模数 26 互质时，才能保证所有明文索引在缩放后仍能一一对应到密文字母，也就是说变换是可逆的。如果 $ a $ 与 26 不互质，就会出现不同明文字母被映射到相同密文位置的情况，导致信息丢失，无法解密还原。

图 4.2 不互质会存在两点加密后落在同一点的情况

代码实现（python）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
from Crypto.Util.number import inverse

class AffineCipher:
    """
    仿射密码
    """
    @staticmethod
    def _process_char(char, b, m, a=None, a_inv=None):
        """对单个字符进行处理"""
        if not a and not a_inv:
            raise ValueError("缺少 a 参数")
        
        if not char.isalpha():
            return char
        
        base = ord('A') if char.isupper() else ord('a')
        index = ord(char) - base
        if a_inv:
            char = (index - b) * a_inv % m
        else:
            char = (a*index + b) % m
        return chr(base + char)
    

    @classmethod
    def encrypt(cls, plaintext, a, b, m):
        return ''.join(cls._process_char(pt, b, m, a) for pt in plaintext)

    @classmethod
    def decrypt(cls, ciphertext, a, b, m):
        a_inv = inverse(a, m)
        return ''.join(cls._process_char(ct, b, m, a_inv=a_inv) for ct in ciphertext)

if __name__ == '__main__':
    original = "Hello, I am DSTBP! 123 456"
    a, b = 11, 5
    encrypted = AffineCipher.encrypt(original, a, b, 26)
    decrypted = AffineCipher.decrypt(encrypted, a, b, 26)

    print(f"原始文本: {original}")
    print(f"加密后: {encrypted}")
    print(f"解密后: {decrypted}")

    '''
    原始文本: Hello, I am DSTBP! 123 456
    加密后: Exwwd, P fh MVGQO! 123 456
    解密后: Hello, I am DSTBP! 123 456
    '''

4.2 攻击手段

4.2.1 已知明文攻击

对于这类密码，如果已知部分明文，只需掌握至少两组明文与密文的对应关系，就有可能推算出关键参数，从而对加密进行有效攻击：

已知明文 $ x_1 $ 对应密文 $ y_1 $；明文 $ x_2 $ 对应密文 $ y_2 $，则有：

$$
\begin{gathered}
y_1 = (ax_1+b) \mod m \
y_2 = (ax_2+b) \mod m
\end{gathered}
$$
两式相减得：

$$
\begin{gathered}
y_1 - y_2 = a(x_1-x_2) \mod m \
a = (y_1 - y_2) \cdot (x_1-x_2)^{-1} \mod m \
b = y_1-ax_1 \mod m
\end{gathered}
$$
代码实现（python）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from Crypto.Util.number import inverse

def known_plaintext_attack(x1, x2, y1, y2, m=26):
    x_inv = inverse(ord(x1) - ord(x2), m)
    a = ((ord(y1) - ord(y2))*(x_inv)) % m
    b = (ord(y1)-a*ord(x1)) % m
    return a, b

if __name__ == "__main__":
    x1, x2 = 'a', 'r'
    y1, y2 = 'z', 'i'
    print(f"仿射密码参数: {known_plaintext_attack(x1, x2, y1, y2)}")

    # 仿射密码参数: (25, 11)

4.2.2 唯密文攻击

现在来探讨只在已知密文的情况下，爆破攻击的可行性。加密参数中，$ a $ 必须与模数 $ m=26 $ 互质，因此 $ a $ 的合法取值为 ${1,\ 3,\ 5,\ 7,\ 9,\ 11,\ 15,\ 17,\ 19,\ 21,\ 23,\ 25}$，共 12 种；而 $ b $ 的取值范围为 0 到 25，共 26 种。除去无加密效果的情况（即 $a=1,\ b=0$ ），有效密钥组合总数为：$12 \times 26 -1 = 311$。

因此，密钥空间非常有限，可在短时间内通过穷举尝试全部组合，完成爆破。

代码实现（python）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
from Crypto.Util.number import inverse


class AffineCipher:
    """
    仿射密码
    """
    @staticmethod
    def _process_char(char, b, m, a=None, a_inv=None):
        """对单个字符进行处理"""
        if not a and not a_inv:
            raise ValueError("缺少 a 参数")
        
        if not char.isalpha():
            return char
        
        base = ord('A') if char.isupper() else ord('a')
        index = ord(char) - base
        if a_inv:
            char = (index - b) * a_inv % m
        else:
            char = (a*index + b) % m
        return chr(base + char)

    @classmethod
    def decrypt(cls, ciphertext, a, b, m):
        a_inv = inverse(a, m)
        return ''.join(cls._process_char(ct, b, m, a_inv=a_inv) for ct in ciphertext)


def ciphertext_only_attack(ciphertext, m=26):
    res = {}
    a_list = [1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23, 25]
    for a in a_list:
        for b in range(0, m):
            res[f'a={a}, b={b}'] = (AffineCipher.decrypt(ciphertext, a, b, m))
    return res

if __name__ == "__main__":
    ciphertext = 'Detts, U ok NIZFJ! 123 456'
    print(f"爆破结果: {ciphertext_only_attack(ciphertext)}")

    '''
    爆破结果: {
        'a=1, b=0': 'Detts, U ok NIZFJ! 123 456', 
        'a=1, b=1': 'Cdssr, T nj MHYEI! 123 456', 
        'a=1, b=2': 'Bcrrq, S mi LGXDH! 123 456', 
        'a=1, b=3': 'Abqqp, R lh KFWCG! 123 456', 
        ...
        'a=17, b=14': 'Hello, I am DSTBP! 123 456',
        ...
        'a=25, b=24': 'Vuffg, E ko LQZTP! 123 456', 
        'a=25, b=25': 'Wvggh, F lp MRAUQ! 123 456'
    }
    '''

补充：从这里也可以看出，仿射密码并不能覆盖所有可能的替换情况（共 $ 26! $ 种），因此它并不适合作为简单替换加密的方式。这也很好理解：简单替换是基于对字母表的任意排列，具有高度随机性，而仿射密码依赖的是可计算的数学公式，替换模式固定，无法实现完全随机的映射。


5. 唯密文攻击 —— 统计分析法

看到这里，你或许会觉得大功告成 —— 只要用简单替换密码（Simple Substitution Cipher）加密信件，便能高枕无忧。但事实真的如此吗？

若密文篇幅较短，在密钥未知的情况下，确实难以破解；可一旦密文足够长，情况就会截然不同。要知道，替换密码依赖固定码表，加密过程中每个字母始终对应唯一字母（比如 A 永远替换为 Z）。这意味着，字母出现的频次在加密前后保持不变：明文中 A 出现 20 次，密文中 Z 便必然出现 20 次。这一特性，就给了攻击者可乘之机。

5.1 破译原理

频率分析（Frequency Analysis）是密码学中常用的分析手段，指通过研究字母或字母组合在文本中出现的频率规律，来辅助破解加密内容。任何语言在书写时，字符出现的频率都具有稳定的分布特征。

例如在英语中，字母 E 最常出现，而 Z 较为少见；常见的字母组合包括 TH、NG、ST、QU，而 QJ、NZ 等组合则极少。在现代汉语中，常用字如“的”“不”“是”出现频率很高，而“翊”“谧”“觑”等字则极为罕见。频率分析正是利用这些分布规律来推测密文中字符的真实含义。

图 5.1 英语语料中的字母频率

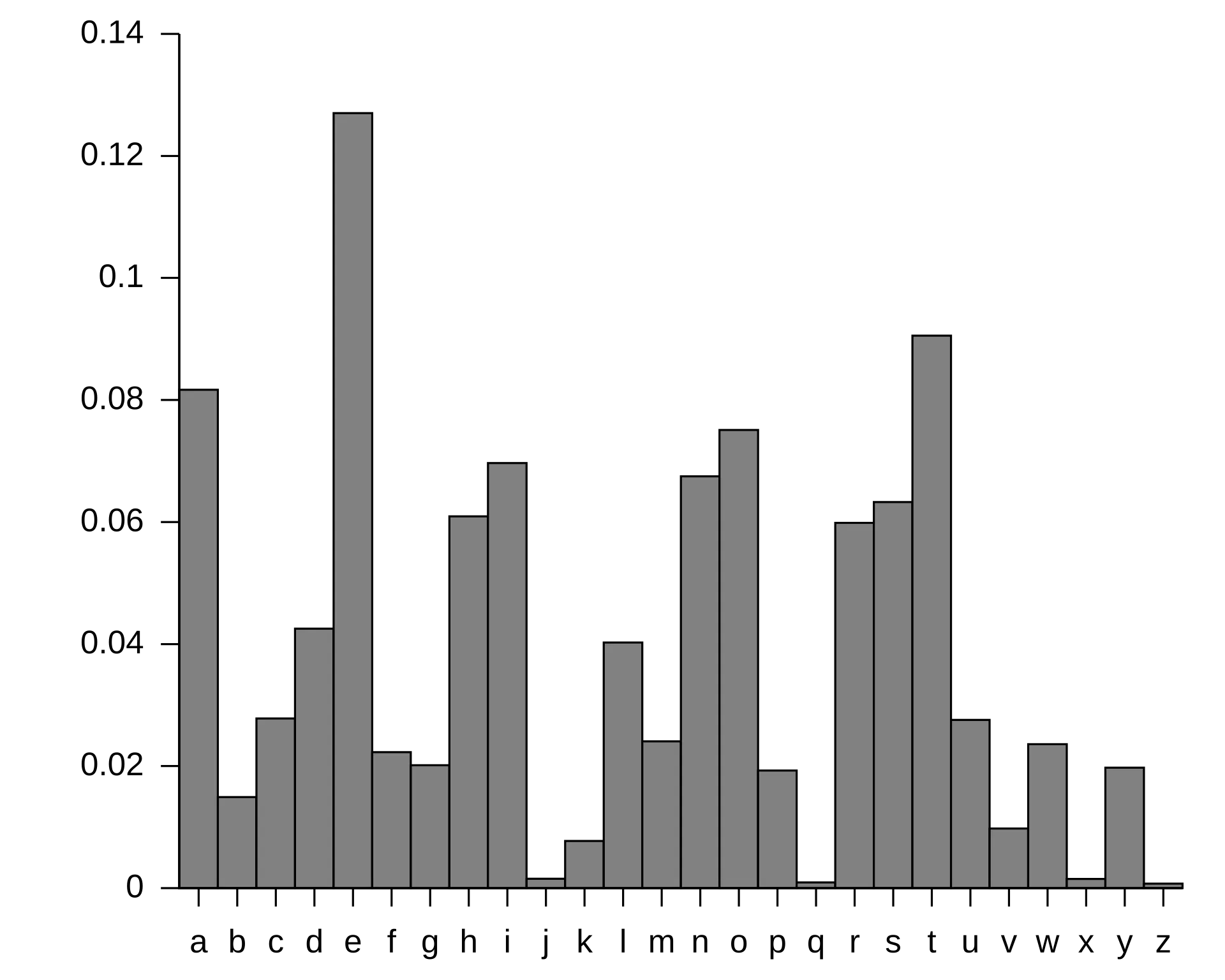
我们只需将密文中频率最高的字母替换成 e、第二高的替换成 t，依次类推，便有极大概率恢复出明文。

5.2 研究背景

自频率分析提出以来，众多研究者不断对其方法进行改进和优化，提出了多种策略以提升其效率。如今，频率分析在破解单表替换密码中的速度和准确性已大幅提高。下面，将简要回顾频率分析的发展历程及其代表成果。

5.2.1 传统频率分析

最基本的频率分析方法是：先统计密文中各字母的出现频率，再将其与目标语言中常见字母的标准频率分布进行一一对应映射，从而推测出明文内容。

然而在实际应用中，频率分析存在显著局限。尽管像 “E”、“T”、“A”、“O” 等字母在英文中通常出现频率较高，但具体分布会因文本类型、主题或写作风格的不同而有所变化。此外，在篇幅较短的文本中，一些字母可能完全不出现，使得频率分布不稳定，降低了分析的准确性和可预测性。

比如《杀死一只知更鸟》第二章前两段的字母频率分布，便能明显看出与标准频率分布并不吻合。

图 5.2 已知统计数据与样本数据之间的字母频率比较

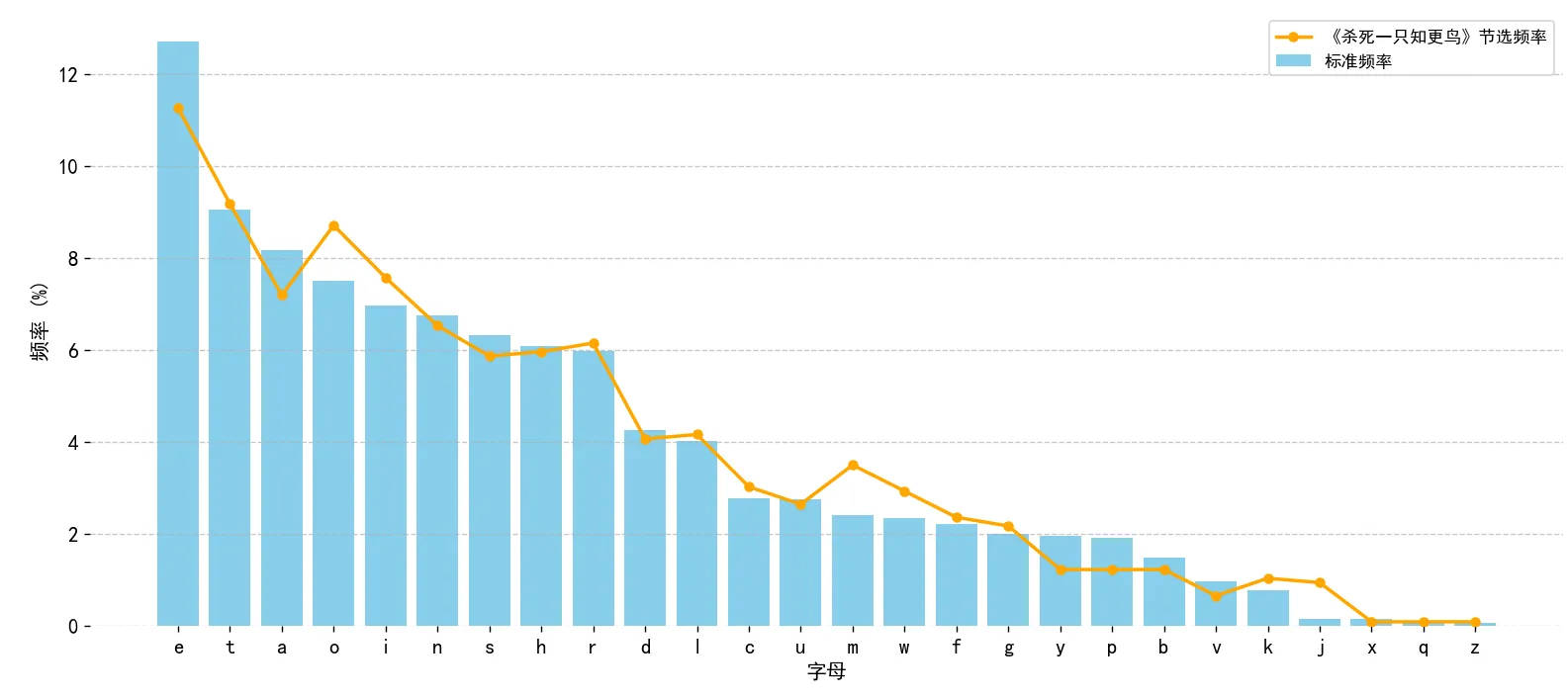
针对这一问题，吴俊斌、吴干华 [1-2] 等学者发现，尽管某些样本的字母频率与标准分布不完全一致，但整体趋势通常相似，且在频率曲线上常出现明显的分界点。例如，字母 e 与 t 之间，或 r 与 d 之间，频率差距显著。基于这一观察，可以将频率分布划分为若干组，并在每组内进行全排列穷举匹配，尝试不同的字母映射组合。每生成一个候选映射表，对密文进行解密，并使用如 nltk 等语料库判断解密结果中合法单词占比，若该占比超过设定阈值，即可认为密文已成功破解。

频率分组 字母 频率范围
极高频率字母组 E ≥ 10%
次高频率字母组 T、A、O、I、N、S、H、R 6% ~ 9%
中等频率字母组 D、L 4% ~ 5%
低频率字母组 C、U、M、W、F、G、Y、P、B 1.5% ~ 3%
极低频率字母组 V、K、J、X、Q、Z < 1%
表 5.1 标准频率分组

通过这种分组策略，原本需要尝试的 $ 26! $ 种情况显著减少，降低到了 $ 8!\times2!\times9!\times6! $。降低了破解的计算复杂度。

代码实现（python）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
import string
from nltk.corpus import words
from itertools import permutations, product
from collections import Counter
from tqdm import tqdm
import time

# 首次使用需要下载词库
# nltk.download('words')


class FrequencyAnalysis:
    def __init__(self, clue: dict = None):
        # 标准英文字母频率分布
        self.letter_freq = {
            'e': 12.702, 't': 9.056, 'a': 8.167, 'o': 7.507, 'i': 6.966, 'n': 6.749, 
            's': 6.327, 'h': 6.094, 'r': 5.987, 'd': 4.253, 'l': 4.025, 'c': 2.782, 
            'u': 2.758, 'm': 2.406, 'w': 2.360, 'f': 2.228, 'g': 2.015, 'y': 1.974, 
            'p': 1.929, 'b': 1.492, 'v': 0.978, 'k': 0.772, 'j': 0.153, 'x': 0.150, 
            'q': 0.095, 'z': 0.074
        }
        
        # 基于频率分界点的分组策略
        self.freq_groups = [
            ['e'],                    # 1! = 1
            ['t', 'a', 'o', 'i', 'n', 's', 'h', 'r'],  # 8! = 40320
            ['d', 'l'],              # 2! = 2
            ['c', 'u', 'm', 'w', 'f', 'g', 'y', 'p', 'b'],  # 9! = 362880
            ['v', 'k', 'j', 'x', 'q', 'z']  # 6! = 720
        ]
        
        self.clue = clue or {}
        self.english_words = set(words.words())

    def get_ciphertext_frequency(self, ciphertext: str):
        """统计密文字符频率"""
        # 只统计字母字符
        letters = [c.lower() for c in ciphertext if c.isalpha()]
        return Counter(letters)

    def calculate_word_ratio(self, text: str):
        """计算文本中合法英文单词的占比"""
        # 清理文本
        translator = str.maketrans('', '', string.punctuation)
        cleaned_text = text.translate(translator)
        words_list = cleaned_text.lower().split()
        
        if not words_list:
            return 0.0
        
        # 统计合法单词
        valid_count = sum(1 for word in words_list if word in self.english_words)
        return round(valid_count / len(words_list), 3)

    def decrypt_text(self, ciphertext: str, mapping: dict):
        """根据映射表解密文本"""
        result = []
        for char in ciphertext:
            if char.isalpha():
                # 查找映射
                for plain_char, cipher_char in mapping.items():
                    if char.lower() == cipher_char:
                        result.append(plain_char.upper() if char.isupper() else plain_char)
                        break
                else:
                    result.append(char)  # 未找到映射，保持原字符
            else:
                result.append(char)
        return ''.join(result)

    def create_mapping(self, plain_groups: list, cipher_groups: list):
        """创建字母映射表"""
        mapping = {}
        
        # 应用已知线索
        for plain_char, cipher_char in self.clue.items():
            mapping[plain_char] = cipher_char
        
        # 根据分组创建映射
        for plain_group, cipher_group in zip(plain_groups, cipher_groups):
            for plain_char, cipher_char in zip(plain_group, cipher_group):
                if plain_char not in self.clue:  # 跳过已知映射
                    mapping[plain_char] = cipher_char
        
        return mapping

    def frequency_analysis(self, ciphertext: str, min_ratio: float = 0.6, show_progress: bool = True):
        """频率分析主函数"""
        print("开始频率分析...")
        start_time = time.time()
        
        # 获取密文字符频率
        cipher_freq = self.get_ciphertext_frequency(ciphertext)
        sorted_cipher_chars = [char for char, _ in cipher_freq.most_common()]
        
        # 按频率分组密文字符
        cipher_groups = []
        start = 0
        for group_size in [1, 8, 2, 9, 6]:
            end = start + group_size
            if start < len(sorted_cipher_chars):
                group = sorted_cipher_chars[start:end]
                cipher_groups.append(group)
                start = end
            else:
                break
        
        print(f"密文字符分组: {cipher_groups}")
        total_combinations = self._calculate_complexity(cipher_groups)
        print(f"计算复杂度: {total_combinations:,} 种组合")
        
        # 生成所有可能的映射组合
        best_result = None
        best_ratio = 0
        tested_count = 0
        
        # 创建进度条
        if show_progress:
            pbar = tqdm(total=total_combinations, desc="破解进度", unit="组合")
        
        for plain_perm in self._generate_group_permutations(cipher_groups):
            mapping = self.create_mapping(plain_perm, cipher_groups)
            decrypted = self.decrypt_text(ciphertext, mapping)
            ratio = self.calculate_word_ratio(decrypted)
            tested_count += 1
            
            if show_progress:
                pbar.update(1)
                pbar.set_postfix({
                    '当前比率': f"{ratio:.3f}",
                    '最佳比率': f"{best_ratio:.3f}",
                    '已测试': f"{tested_count:,}"
                })
            
            if ratio > best_ratio:
                best_ratio = ratio
                best_result = {
                    'text': decrypted,
                    'mapping': mapping,
                    'ratio': ratio
                }
                
                if ratio >= min_ratio:
                    if show_progress:
                        pbar.close()
                    elapsed_time = time.time() - start_time
                    print(f"\n找到高质量结果 (比率: {ratio:.3f})")
                    print(f"耗时: {elapsed_time:.2f}秒")
                    print(f"映射: {mapping}")
                    print(f"明文: {decrypted[:200]}...")
                    return best_result
        
        if show_progress:
            pbar.close()
        
        elapsed_time = time.time() - start_time
        print(f"\n总耗时: {elapsed_time:.2f}秒")
        print(f"测试了 {tested_count:,} 种组合")
        
        if best_result:
            print(f"\n最佳结果 (比率: {best_ratio:.3f}):")
            print(f"映射: {best_result['mapping']}")
            print(f"明文: {best_result['text']}")
        else:
            print("未找到满意的解密结果")
        
        return best_result

    def _generate_group_permutations(self, cipher_groups):
        """生成所有可能的明文分组排列"""
        group_permutations = []
        
        for i, cipher_group in enumerate(cipher_groups):
            plain_group = self.freq_groups[i]
            if len(plain_group) == len(cipher_group):
                perms = list(permutations(plain_group))
                group_permutations.append(perms)
            else:
                # 如果长度不匹配，使用原始顺序
                group_permutations.append([plain_group])
        
        # 生成所有组合
        for combo in product(*group_permutations):
            yield list(combo)

    def _calculate_complexity(self, cipher_groups):
        """计算计算复杂度"""
        total_combinations = 1
        for i, group in enumerate(cipher_groups):
            if i < len(self.freq_groups):
                plain_group = self.freq_groups[i]
                if len(group) == len(plain_group):
                    total_combinations *= len(list(permutations(plain_group)))
        
        return total_combinations


if __name__ == '__main__':
    ciphertext = '''Gann niuc vr ipknw af Rixciohik, cd kicvkf cd Oikagapf1. Ti rpt eao duu df cei uasi d'qndqlhvr pfg A tpr oarikphni2 tacedvc eao vfcan ac dqqvkkig cd oi cepc A tdvng hi rcpkcafm cdrqeddn af p tiil. A fisik nddlig udktpkg odki cd pfwceafm af ow naui. Edvkr du tafcikcaoiepg udvfg oi af cei ckiiedvri, nddlafm dsik pc cei rqeddnwpkg, rxwafm df ovncacvgir duqeangkif cekdvme p ctd-xdtik cinirqdxi Yio epg masif oi, nipkfafm ceiak mpoir,udnndtafm Yio'r kig ypqlic cekdvme tkammnafm3 qakqnir du hnafg opf'r hvuu, riqkicnw repkafmceiak oarudkcvfir pfg oafdk4 saqcdkair. A ndfmig cd ydaf ceio.
Yio qdfgirqifgig5 cd cpli oi cd rqeddn cei uakrc gpw, p ydh vrvpnnw gdfi hw dfi'rxpkifcr, hvc Pccaqvr epg rpag Yio tdvng hi ginamecig cd redt oi teiki ow kddo tpr. Aceafl rdoi odfiw qepfmig epfgr af cear ckpfrpqcadf, udk pr ti ckdccig6 pkdvfg ceiqdkfik xprc cei Kpgniw Xnpqi A eipkg pf vfupoanapk7 yafmni8 af Yio'r xdqlicr. Teif tirndtig cd p tpnl pc cei igmi du cei rqeddnwpkg, Yio tpr qpkiuvn cd izxnpaf cepc gvkafmrqeddn edvkr A tpr fdc cd hdceik eao, A tpr fdc cd pxxkdpqe eao tace kijvircr cd ifpqc9 pqepxcik du Cpkbpf pfg cei Pfc Oif, cd iohpkkprr eao tace kiuikifqir cd ear xkaspci naui,dk cpm pndfm hieafg eao pc kiqirr10 pfg fddf. A tpr cd rcaql tace cei uakrc mkpgi pfg eitdvng rcaql tace cei uauce. Af redkc, A tpr cd nipsi eao pndfi.'''
    
    # 创建频率分析器实例
    fa = FrequencyAnalysis()
    
    # 执行频率分析
    result = fa.frequency_analysis(ciphertext, min_ratio=0.5, show_progress=True)
    
    if result:
        print(f"\n最终结果:")
        print(f"单词匹配率: {result['ratio']:.3f}")
        print(f"解密文本: {result['text']}")
    else:
        print("未找到满意的解密结果")

5.2.2 候选密钥+词典匹配频率分析

尽管传统频率分析已大幅减少尝试次数，但计算量仍然庞大。为进一步提高效率，可以结合单词频率分析来辅助破解。比如说：先识别密文中出现频率最高的符号，假设它对应字母 e，并进行初步替换；接着查找密文中出现的单字母单词，尝试替换为常见的 a 或 I；然后分析包含 e 的高频单词结构，如 “the”、”that”、”who”、”is” 等，逐步推测其他字母的替换关系。

通过不断匹配已知高频英文单词，并据此反推出潜在的替换规则，再将更新后的假设应用于密文，循环修正、验证，直到成功还原原文。

Kang 等人[3] 与 2024 年提出一种基于候选密钥+词典匹配的频率分析方法，具体操作如下：

首先，通过对密文进行字母频率分析，并与标准频率分布进行对应，构造一个初始密钥。接下来，为了让这个初始密钥更精确，系统执行下面优化算法：

  1. 在初始密钥基础上，随机交换映射表中两个字母，计算一个评价函数评估新密钥的解密效果[4]。
    $$
    f(t)=\sum_{i,\ j}|D_{ij}(t)-E_{ij}|
    $$
    其中 $ D(t) $ 和 $ E $ 是 $ 26 \times 26 $ 的矩阵，分别表示给定文本 $ t $ 的双字母频率和英语字母常见双字母频率[5]。

    图 5.3 双字母频率分布表

    遍历矩阵索引并比较这些频率，如果 $ f(t) $ 减少，表示新组合的效果更好，更接近标准频率，解密结果更像英文。就用新密钥替换旧密钥，重复 3000 次，得到优化后的密钥。（大约 3000 次后，$ f(t) $ 趋于收敛）

  2. 考虑随机性带来的结果差异，算法会生成多个候选密钥，以覆盖更大可能空间。（作者发现生成 10 个密钥就能覆盖较好的解密可能性）

  3. 将密文中非字母字符（如引号、标点）转成空格，并按空格切分成密文单词片段（tokens）。分别用每个候选密钥对其解密。

  4. 接入词典 API。对每个解密结果，查找相似的英文单词，并用一个打分函数来评估每个单词的可信度。打分函数考虑三个因素：

    • 相似单词在其他候选结果中出现的次数（出现越多越可信）
    • 词的流行程度（由词典 API 给出，流行度越高越可信）
    • 单词长度（越长、越具体越可信）

    三个因素综合成一个打分值 $ S $，用来衡量该解密结果更像哪个真实词。

$$
S=count \times (1+\log_{10}(reputation)) \times length
$$

  1. 将每个 token 与其最接近的真实单词组成的元组列表按打分值 $ S $ 排序。对得分高的 token，优先尝试用其对应的真实单词反推替换密钥，并据此逐步修正整体映射关系。具体操作如下：
    • 如果当前 token 长度 < 4，先不处理，防止出错。
    • 如果替换不冲突，更新密钥。
    • 如果冲突，保留空位，后续再尝试其它 token 处理。
  2. 最终，系统输出与真实英文最接近的解密结果所对应的密钥。若密文未涵盖全部 26 个字母，或推导出的密钥存在缺失，系统将对剩余未出现的字母进行全排列补全。由于缺失字母数量有限，这部分爆破尝试次数在可接受范围内。
图 5.4 基于候选密钥+词典匹配的频率分析流程图

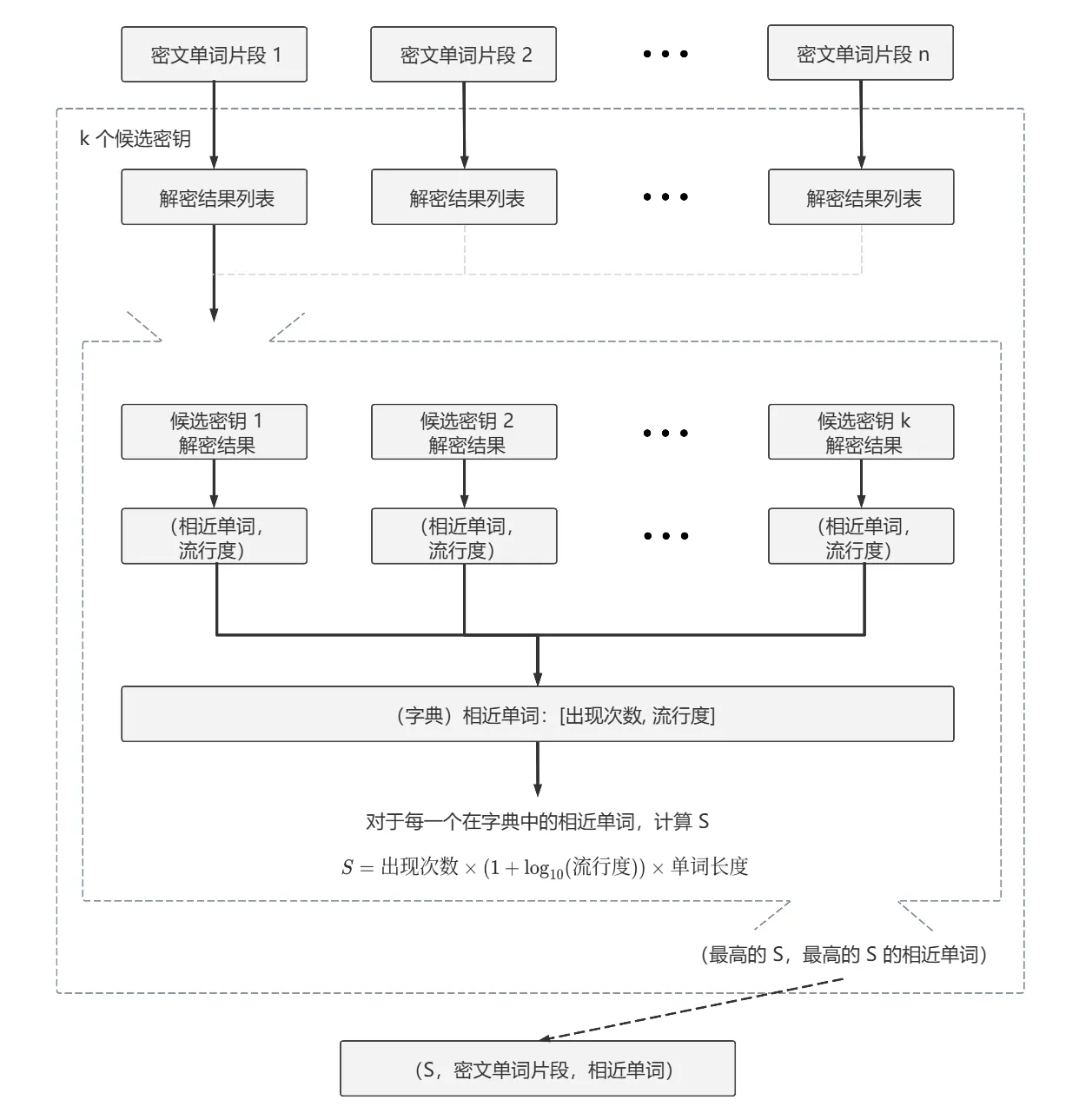
该方法的优势在于：它适用于短密文，即使缺乏足够的统计特征也能发挥作用；不依赖大量训练数据或上下文信息；同时通过利用自然语言特征，如常见单词和拼写规则，有效提升了解密的准确性，并能在有限时间内解出密文。

代码实现（python）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
import re
import json
import random
import wordfreq
import numpy as np
from collections import Counter
from autocorrect import Speller
from nltk.corpus import words
from itertools import permutations
from string import punctuation
from typing import Dict, List, Tuple, Optional
from pathlib import Path

# 首次使用需要下载词库
# nltk.download('words')

class FrequencyAnalysis:
    """频率分析类 - 用于破解替换密码"""
    
    # 标准英文字母频率分布
    LETTER_FREQ = {
        'e': 12.702, 't': 9.056, 'a': 8.167, 'o': 7.507, 'i': 6.966, 'n': 6.749, 
        's': 6.327, 'h': 6.094, 'r': 5.987, 'd': 4.253, 'l': 4.025, 'c': 2.782, 
        'u': 2.758, 'm': 2.406, 'w': 2.360, 'f': 2.228, 'g': 2.015, 'y': 1.974, 
        'p': 1.929, 'b': 1.492, 'v': 0.978, 'k': 0.772, 'j': 0.153, 'x': 0.150, 
        'q': 0.095, 'z': 0.074
    }
    
    def __init__(self, clue: Dict[str, str] = None, bigram_file: str = None):
        """
        初始化频率分析器
        """
        self.clue = clue or {}
        self.english_words = set(words.words())
        self.speller = Speller(lang='en')
        
        # 字母映射表
        self.letter_to_index = {letter: i for i, letter in enumerate('abcdefghijklmnopqrstuvwxyz')}
        self.index_to_letter = {i: letter for i, letter in enumerate('abcdefghijklmnopqrstuvwxyz')}
        
        # 加载双字母频率矩阵
        self.expected_bigram_matrix = self._load_bigram_matrix(bigram_file)
    
    def _load_bigram_matrix(self, file_path: Optional[str] = None) -> np.ndarray:
        """加载双字母频率矩阵"""
        if file_path is None:
            file_path = Path(__file__).parent / 'bigram_frequency_matrix.json'
        
        try:
            with open(file_path, 'r') as f:
                data = json.load(f)
                return np.array(data['matrix'])
        except FileNotFoundError:
            print(f"警告: 未找到双字母频率矩阵文件 {file_path}")
            return np.ones((26, 26)) * 0.01
    
    def analyze_frequency(self, text: str) -> Dict[str, float]:
        """分析文本中字母频率"""
        letters = [c.lower() for c in text if c.isalpha()]
        if not letters:
            return {}
        
        counter = Counter(letters)
        total = len(letters)
        return {char: (count / total) * 100 for char, count in counter.items()}
    
    def get_bigram_matrix(self, text: str) -> np.ndarray:
        """计算文本的双字母频率矩阵"""
        matrix = np.zeros((26, 26))
        letters = [c.lower() for c in text if c.isalpha()]
        
        # 统计双字母频率
        for i in range(len(letters) - 1):
            first, second = letters[i], letters[i + 1]
            if first in self.letter_to_index and second in self.letter_to_index:
                row = self.letter_to_index[first]
                col = self.letter_to_index[second]
                matrix[row][col] += 1
        
        # 归一化
        total = np.sum(matrix)
        return (matrix / total * 100) if total > 0 else matrix
    
    def decrypt_text(self, ciphertext: str, mapping: Dict[str, str]) -> str:
        """根据映射表解密文本"""
        result = []
        for char in ciphertext:
            if char.isalpha():
                # 查找映射
                for plain_char, cipher_char in mapping.items():
                    if char.lower() == cipher_char:
                        result.append(plain_char.upper() if char.isupper() else plain_char)
                        break
                else:
                    result.append(char)
            else:
                result.append(char)
        return ''.join(result)
    
    def create_initial_mapping(self, cipher_freq: Dict[str, float]) -> Dict[str, str]:
        """基于频率分析创建初始映射"""
        # 按频率排序
        sorted_cipher = sorted(cipher_freq.items(), key=lambda x: x[1], reverse=True)
        sorted_standard = sorted(self.LETTER_FREQ.items(), key=lambda x: x[1], reverse=True)
        
        mapping = {}
        
        # 应用已知线索
        for plain_char, cipher_char in self.clue.items():
            mapping[plain_char] = cipher_char
        
        # 根据频率对应创建映射
        cipher_chars = [char for char, _ in sorted_cipher]
        standard_chars = [char for char, _ in sorted_standard]
        
        for cipher_char, standard_char in zip(cipher_chars, standard_chars):
            if standard_char not in self.clue:
                mapping[standard_char] = cipher_char
        
        return mapping
    
    def evaluate_mapping(self, ciphertext: str, mapping: Dict[str, str]) -> float:
        """评价映射质量"""
        decrypted_text = self.decrypt_text(ciphertext, mapping)
        actual_matrix = self.get_bigram_matrix(decrypted_text)
        difference = np.abs(actual_matrix - self.expected_bigram_matrix)
        return np.sum(difference)
    
    def swap_random_chars(self, mapping: Dict[str, str]) -> Dict[str, str]:
        """随机交换映射表中的两个字母"""
        new_mapping = mapping.copy()
        available_chars = [char for char in mapping.keys() if char not in self.clue]
        
        if len(available_chars) < 2:
            return mapping
        
        char1, char2 = random.sample(available_chars, 2)
        cipher1, cipher2 = new_mapping[char1], new_mapping[char2]
        new_mapping[char1], new_mapping[char2] = cipher2, cipher1
        
        return new_mapping
    
    def optimize_mapping(self, ciphertext: str, initial_mapping: Dict[str, str], 
                        iterations: int = 3000) -> Dict[str, str]:
        """使用模拟退火算法优化映射"""
        current_mapping = initial_mapping.copy()
        current_score = self.evaluate_mapping(ciphertext, current_mapping)
        best_mapping = current_mapping.copy()
        best_score = current_score
        
        for i in range(iterations):
            new_mapping = self.swap_random_chars(current_mapping)
            new_score = self.evaluate_mapping(ciphertext, new_mapping)
            
            # 接受更好的解
            if new_score < current_score:
                current_mapping = new_mapping
                current_score = new_score
                
                if new_score < best_score:
                    best_mapping = new_mapping.copy()
                    best_score = new_score
        
        return best_mapping
    
    def generate_candidates(self, ciphertext: str, initial_mapping: Dict[str, str], 
                          num_candidates: int = 10, iterations: int = 3000) -> List[Dict[str, str]]:
        """生成多个候选映射"""
        candidates = []
        
        for i in range(num_candidates):
            random.seed(i + 42)  # 确保多样性
            candidate = self.optimize_mapping(ciphertext, initial_mapping, iterations)
            candidates.append(candidate)
        
        return candidates
    
    def tokenize_text(self, text: str) -> List[str]:
        """将文本分割成单词片段"""
        processed = re.sub(r'[^a-zA-Z]', ' ', text)
        processed = re.sub(r'\s+', ' ', processed).strip()
        return processed.split()
    
    def find_similar_word(self, token: str) -> Tuple[str, float]:
        """查找相似单词并返回频率"""
        similar_word = self.speller(token)
        reputation = wordfreq.word_frequency(similar_word, 'en')
        return similar_word, reputation
    
    def score_token_candidates(self, token: str, candidates: List[Dict[str, str]]) -> Dict:
        """对token的所有候选解密结果进行评分"""
        token_results = []
        
        for candidate in candidates:
            decrypted = self.decrypt_text(token, candidate)
            similar_word, reputation = self.find_similar_word(decrypted)
            
            token_results.append({
                'token': token,
                'similar_word': similar_word,
                'reputation': reputation
            })
        
        # 统计单词出现次数
        word_counts = Counter(result['similar_word'] for result in token_results)
        
        # 计算综合评分
        best_result = max(token_results, key=lambda x: 
            word_counts[x['similar_word']] * (1 + x['reputation']) * len(x['similar_word']))
        
        return best_result
    
    def create_token_mapping(self, token: str, word: str) -> Dict[str, str]:
        """根据token和对应单词创建字母映射"""
        if len(token) != len(word):
            return {}
        
        mapping = {}
        for cipher_char, plain_char in zip(token.lower(), word.lower()):
            if cipher_char.isalpha() and plain_char.isalpha():
                mapping[plain_char] = cipher_char
        
        return mapping
    
    def check_mapping_conflicts(self, new_mapping: Dict[str, str], 
                              current_mapping: Dict[str, str]) -> List[str]:
        """检查映射冲突"""
        conflicts = []
        
        for plain_char, cipher_char in new_mapping.items():
            # 检查键冲突
            if plain_char in current_mapping and current_mapping[plain_char] != cipher_char:
                conflicts.append(f"键冲突: '{plain_char}' 已映射到 '{current_mapping[plain_char]}'")
            
            # 检查值冲突
            for existing_plain, existing_cipher in current_mapping.items():
                if existing_cipher == cipher_char and existing_plain != plain_char:
                    conflicts.append(f"值冲突: '{cipher_char}' 已被 '{existing_plain}' 映射")
        
        return conflicts
    
    def merge_mappings(self, current_mapping: Dict[str, str], 
                      new_mapping: Dict[str, str]) -> Tuple[Dict[str, str], bool]:
        """安全地合并映射"""
        conflicts = self.check_mapping_conflicts(new_mapping, current_mapping)
        
        if conflicts:
            return current_mapping, False
        
        merged = current_mapping.copy()
        merged.update(new_mapping)
        return merged, True
    
    def refine_mapping_with_tokens(self, tokens: List[str], 
                                  candidates: List[Dict[str, str]]) -> Dict[str, str]:
        """基于高分token优化映射"""
        # 处理所有token
        token_results = []
        for token in tokens:
            result = self.score_token_candidates(token, candidates)
            token_results.append(result)
        
        # 按评分排序
        token_results.sort(key=lambda x: 
            wordfreq.word_frequency(x['similar_word'], 'en') * len(x['similar_word']), reverse=True)
        
        current_mapping = {}
        
        # 处理长token（>=4字符）
        for result in token_results:
            if len(result['token']) >= 4:
                new_mapping = self.create_token_mapping(result['token'], result['similar_word'])
                current_mapping, success = self.merge_mappings(current_mapping, new_mapping)
        
        # 处理短token
        for result in token_results:
            if len(result['token']) < 4:
                new_mapping = self.create_token_mapping(result['token'], result['similar_word'])
                current_mapping, success = self.merge_mappings(current_mapping, new_mapping)
        
        return current_mapping
    
    def calculate_word_ratio(self, text: str) -> float:
        """计算文本中合法英文单词的占比"""
        translator = str.maketrans('', '', punctuation)
        cleaned_text = text.translate(translator)
        words_list = cleaned_text.lower().split()
        
        if not words_list:
            return 0.0
        
        valid_count = sum(1 for word in words_list if word in self.english_words)
        return round(valid_count / len(words_list), 3)
    
    def complete_mapping(self, partial_mapping: Dict[str, str]) -> List[Dict[str, str]]:
        """补全缺失的字母映射"""
        all_letters = set('abcdefghijklmnopqrstuvwxyz')
        used_keys = set(partial_mapping.keys())
        used_values = set(partial_mapping.values())
        
        missing_keys = all_letters - used_keys
        available_values = all_letters - used_values
        
        if len(missing_keys) != len(available_values):
            return []
        
        # 生成所有可能的排列
        mappings = []
        for perm in permutations(sorted(available_values)):
            full_mapping = partial_mapping.copy()
            for key, value in zip(sorted(missing_keys), perm):
                full_mapping[key] = value
            mappings.append(full_mapping)
        
        return mappings
    
    def brute_force_completion(self, ciphertext: str, partial_mapping: Dict[str, str]) -> str:
        """暴力破解补全映射"""
        mappings = self.complete_mapping(partial_mapping)
        
        best_text = ""
        best_ratio = 0.0
        
        for mapping in mappings:
            decrypted = self.decrypt_text(ciphertext, mapping)
            ratio = self.calculate_word_ratio(decrypted)
            
            if ratio > best_ratio:
                best_ratio = ratio
                best_text = decrypted
                best_mapping = mapping
        
        return best_text, best_mapping
    
    def analyze(self, ciphertext: str, use_brute_force: bool = False) -> str:
        """主分析函数"""
        print("[+] 开始频率分析...")
        
        # 初始频率分析
        cipher_freq = self.analyze_frequency(ciphertext)
        initial_mapping = self.create_initial_mapping(cipher_freq)
        
        # 生成候选映射
        print("[+] 生成候选映射...")
        candidates = self.generate_candidates(ciphertext, initial_mapping)
        
        # 处理token
        print("[+] 处理单词片段...")
        tokens = self.tokenize_text(ciphertext)
        refined_mapping = self.refine_mapping_with_tokens(tokens, candidates)
        
        print(f"[+] 优化后的映射: {refined_mapping}")
        
        # 最终解密
        if use_brute_force and len(refined_mapping) < 26:
            print("[+] 使用暴力破解补全映射...")
            result, refined_mapping = self.brute_force_completion(ciphertext, refined_mapping)
        else:
            result = self.decrypt_text(ciphertext, refined_mapping)
        
        print(f"[+] 解密结果: {result}")
        print(f"[+] 解密密钥: {refined_mapping}")
        return result


if __name__ == "__main__":
    ciphertext = '''Teif A tpr ctifcw-risif wipkr dng, A tpr p oafafm-hkdlik’r qnikl af Rpf Ukpfqarqd, pfg pf izxikc af pnn cei gicpanr du rcdql ckpuuaq. A tpr pndfi af cei tdkng, pfg epg fdceafm cd gixifg vxdf hvc ow tacr pfg p qnipf kixvcpcadf; hvc ceiri tiki riccafm ow uiic af cei kdpg cd isifcvpn udkcvfi, pfg A tpr qdfcifc tace cei xkdrxiqc.'''
    
    analyzer = FrequencyAnalysis()
    result = analyzer.analyze(ciphertext, use_brute_force=True)

    '''
    [+] 开始频率分析...
    [+] 生成候选映射...
    [+] 处理单词片段...
    [+] 优化后的映射: {'t': 'c', 'h': 'e', 'e': 'i', 'r': 'r', 'w': 't', 'n': 'f', 'g': 'm', 'i': 'a', 'o': 'd', 'm': 'u', 'a': 'p', 'l': 'n', 'y': 'w', 'v': 's', 'u': 'v', 'b': 'h', 'd': 'g'}
    [+] 使用暴力破解补全映射...
    [+] 解密结果: When I war twenty-reven yeasr old, I war a qining-bsokes’r clesk in Ran Msancirco, and an ezpest in all the detailr om rtock tsammic. I war alone in the wosld, and had nothing to depend upon but qy witr and a clean seputation; but there wese retting qy meet in the soad to eventual mostune, and I war content with the psorpect.
    [+] 解密密钥: {'t': 'c', 'h': 'e', 'e': 'i', 'r': 'r', 'w': 't', 'n': 'f', 'g': 'm', 'i': 'a', 'o': 'd', 'm': 'u', 'a': 'p', 'l': 'n', 'y': 'w', 'v': 's', 'u': 'v', 'b': 'h', 'd': 'g', 'c': 'q', 'f': 'b', 'j': 'j', 'k': 'l', 'p': 'x', 'q': 'o', 's': 'k', 'x': 'y', 'z': 'z'}
    '''
1
{"letters":"abcdefghijklmnopqrstuvwxyz","matrix":[[0.00283,0.229786,0.447772,0.367956,0.012397,0.074207,0.204725,0.013643,0.316448,0.011753,0.104699,1.08745,0.284866,1.985151,0.004626,0.202846,0.002244,1.074898,0.871095,1.486732,0.119033,0.204933,0.059916,0.018839,0.217361,0.011869],[0.146204,0.010933,0.00189,0.002474,0.576284,0.000146,0.000255,0.001057,0.106597,0.023225,9.4e-05,0.2334,0.003129,0.002095,0.195411,0.000547,1.2e-05,0.11156,0.045832,0.017104,0.184944,0.003844,0.000295,2.8e-05,0.176468,3.6e-05],[0.538164,0.00063,0.083138,0.002231,0.651417,0.001408,0.000886,0.597766,0.281485,0.000105,0.117626,0.149011,0.002665,0.00086,0.79386,0.001315,0.005475,0.149456,0.022823,0.460972,0.162614,0.000208,0.000139,3.1e-05,0.041719,0.000731],[0.151067,0.002773,0.002519,0.042751,0.764818,0.002779,0.031003,0.005438,0.492966,0.004782,0.000337,0.03234,0.018177,0.007569,0.188235,0.001733,0.000707,0.08545,0.126261,0.002896,0.148461,0.019053,0.008162,4.6e-05,0.050423,7.8e-05],[0.688165,0.027074,0.477283,1.168123,0.377605,0.162732,0.119536,0.026324,0.183352,0.004546,0.016472,0.530302,0.373664,1.454248,0.0725,0.171574,0.057252,2.048265,1.339394,0.412608,0.031153,0.254784,0.116806,0.214045,0.143746,0.004523],[0.164,0.000274,0.000576,0.000495,0.236573,0.146317,0.000512,0.000183,0.284586,7.3e-05,0.000117,0.064905,0.000686,0.000419,0.487754,0.000222,5e-06,0.213189,0.00551,0.081664,0.095975,2.9e-05,0.000229,2.9e-05,0.009098,9e-06],[0.148077,0.000495,0.000229,0.00316,0.38519,0.001204,0.024755,0.227503,0.151637,3.9e-05,0.00026,0.060637,0.009858,0.065639,0.132128,0.000412,1.2e-05,0.196778,0.051193,0.015403,0.08577,4.2e-05,0.000648,2e-05,0.02594,0.000122],[0.925764,0.00439,0.001228,0.002857,3.074741,0.002243,0.000276,0.000522,0.763242,4.5e-05,0.000234,0.012592,0.012743,0.025758,0.484902,0.000592,0.000423,0.084393,0.014684,0.130186,0.073693,0.000223,0.004774,9e-06,0.050089,0.000381],[0.286282,0.098603,0.698707,0.295504,0.384646,0.203257,0.254961,0.002091,0.022782,0.001111,0.042913,0.431535,0.31776,2.432745,0.834932,0.089211,0.011304,0.315172,1.12843,1.123274,0.017409,0.287848,0.000625,0.022032,0.000222,0.06434],[0.025861,7.5e-05,0.000122,9.3e-05,0.051887,8.6e-05,3.7e-05,0.000126,0.002763,0.000106,6.2e-05,0.000113,0.00013,0.000147,0.05379,0.000217,0.0,0.000243,0.000118,0.000103,0.058702,6.1e-05,4.1e-05,6e-06,4e-05,8e-06],[0.016956,0.000901,0.000224,0.00067,0.213768,0.001587,0.002563,0.003185,0.097878,0.000123,0.000453,0.01057,0.001789,0.051439,0.006076,0.000727,7e-06,0.002722,0.047509,0.001033,0.003026,0.000157,0.002178,2e-05,0.00595,5e-06],[0.527529,0.00669,0.011822,0.252606,0.829254,0.053477,0.006088,0.001619,0.624352,0.000112,0.019715,0.576571,0.023021,0.00587,0.386884,0.01903,0.000127,0.010051,0.141513,0.123637,0.135189,0.034906,0.012639,0.000305,0.425014,0.000417],[0.565269,0.090256,0.004312,0.000671,0.793006,0.003818,0.001225,0.000533,0.317691,0.000104,0.00014,0.004607,0.096069,0.00879,0.336878,0.239175,2.5e-05,0.003106,0.092833,0.001367,0.114619,0.00029,0.000584,3.5e-05,0.062186,3.4e-05],[0.347235,0.004336,0.415746,1.352281,0.691722,0.067181,0.953015,0.010884,0.339212,0.011086,0.051605,0.063784,0.027749,0.072765,0.464575,0.006036,0.00595,0.009152,0.508937,1.041251,0.078644,0.052007,0.005797,0.002621,0.097917,0.004369],[0.057486,0.096671,0.166405,0.195449,0.038631,1.174975,0.094024,0.021354,0.087751,0.006976,0.064312,0.365493,0.546257,1.758046,0.210259,0.223911,0.001037,1.276539,0.289967,0.442103,0.870002,0.178087,0.330478,0.018575,0.036181,0.003472],[0.323572,0.001309,0.001176,0.001199,0.477989,0.001455,0.000474,0.09439,0.123094,0.0001,0.000819,0.262987,0.015956,0.001189,0.361373,0.136546,3.8e-05,0.474471,0.054571,0.105782,0.10454,0.000221,0.001207,5.2e-05,0.011764,0.000226],[0.000152,3.8e-05,4e-05,1.8e-05,2e-05,3.4e-05,0.0,9e-06,0.000318,8e-06,0.0,0.000238,3.5e-05,6.6e-05,4.7e-05,1e-05,6.1e-05,6.2e-05,0.000158,4.9e-05,0.147541,2.3e-05,6e-06,6e-06,0.0,0.0],[0.685633,0.026712,0.121387,0.189316,1.854323,0.03226,0.099773,0.015112,0.727619,0.000553,0.097034,0.086265,0.175133,0.160361,0.726724,0.04162,0.000998,0.120743,0.396527,0.361676,0.128329,0.069283,0.012757,0.00117,0.24774,0.000638],[0.218017,0.007916,0.154749,0.005259,0.932115,0.017164,0.002468,0.31524,0.550057,0.00027,0.039465,0.055881,0.065199,0.009175,0.397732,0.191254,0.007444,0.00599,0.405075,1.053476,0.311177,0.001241,0.023528,1.8e-05,0.056845,0.00025],[0.529886,0.002544,0.026136,0.001296,1.20487,0.005661,0.001969,3.556203,1.342579,0.000112,0.000464,0.098449,0.026479,0.010011,1.041267,0.004294,8.9e-05,0.42582,0.337488,0.170683,0.254907,0.001163,0.082372,0.000118,0.227277,0.003849],[0.136333,0.08858,0.187652,0.091401,0.14748,0.018532,0.127908,0.001067,0.101153,0.000516,0.004604,0.345829,0.138383,0.394413,0.010657,0.136012,0.000257,0.542748,0.454257,0.405151,0.00078,0.002917,0.000277,0.003935,0.004567,0.001911],[0.13998,8.9e-05,0.000233,0.000299,0.825281,5.5e-05,0.000105,9.5e-05,0.269544,2.6e-05,1.2e-05,0.000412,0.000113,0.000153,0.071107,0.000195,8e-06,0.000876,0.000577,0.000219,0.002212,9.3e-05,2.6e-05,1.6e-05,0.004897,1.8e-05],[0.385337,0.001061,0.000674,0.003538,0.360899,0.001608,9.8e-05,0.378793,0.374421,3.2e-05,0.001067,0.015221,0.00109,0.078988,0.221754,0.000744,0.0,0.030761,0.035084,0.006541,0.000695,1.4e-05,0.000262,5e-06,0.002425,0.0],[0.029601,7.7e-05,0.02646,6e-06,0.021795,0.001857,1.9e-05,0.004171,0.039418,1.8e-05,1e-05,0.000593,0.000233,5.7e-05,0.002699,0.066864,0.000292,3.2e-05,6.4e-05,0.046661,0.004771,0.001953,0.000223,0.002804,0.002576,5e-06],[0.015766,0.004299,0.013501,0.006818,0.092669,0.000754,0.002593,0.000521,0.02882,2e-05,0.00033,0.014756,0.023675,0.013214,0.149902,0.024914,1.4e-05,0.007792,0.096832,0.016684,0.001328,0.000181,0.003372,0.000149,7.1e-05,0.001812],[0.024904,0.000208,7.5e-05,5e-05,0.049733,2.2e-05,0.000168,0.000666,0.012117,1.1e-05,3.2e-05,0.001257,0.000167,0.000153,0.007181,4.8e-05,3.2e-05,0.000189,0.000298,0.000235,0.002152,0.000164,0.000223,4e-06,0.002357,0.00266]]}

结语

雨还在下，敲得窗棂愈发急促。当你将用单表替换密码加密的信件封入火漆信封时，指腹仍能感受到羊皮纸的粗糙纹理 —— 那些被重新编排的字母虽暂时守住了秘密，却像悬在头顶的利剑。

你深知，这些看似巧妙的替换并非无懈可击。凯撒的偏移量不过二十余种可能，即便是最复杂的简单替换，也难敌字母频率的无情破译。当对手用统计规律撬开替换表的缝隙时，再精密的单表映射也会沦为透明。就像此刻窗缝里钻进来的风，总能找到最细微的缺口。

商队的船帆即将再次升起，英吉利海峡的雾气中藏着更多窥探的眼睛。或许，该让字母的替换不再墨守成规？让每个字符在不同位置拥有不同的替身，如同信使在不同港口更换不同的纹章。

雨势渐歇时，你在羊皮纸的空白处写下一行字：“若一张表不足为恃，便以百张表应之。”远处的航标灯在雾中明灭，仿佛在预示着一种更复杂的加密之道……


参考

参考资料：

https://zh.wikipedia.org/wiki/ROT13

Keyed Caesar Cipher Tool

阿特巴希密码 维基百科

CacheSleuth

字母频率 维基百科

【科普】从单表代换到字频分析

English bigram and letter pair frequencies from the Google Corpus Data in JSON format


参考文献：

[1] 吴干华.基于频率分析的代替密码破译方法及其程序实现[J].福建电脑,2006,(09):125+127.

[2] 吴俊斌,吴晟,吴兴蛟. 基于字母频率的单表替换密码破译算法[J]. 计算机与数字工程,2016,(4): 583-585，634.

[3] Kang, DayeongCAa,Lee,et al. A Robust Decryption Technique Using Letter Frequency Analysis for Short Monoalphabetic Substitution Ciphers[J]. Journal of Computing Science and Engineering, 2024,Vol.18(3): 144-151.

[4] Thomas Jakobsen,. A fast method for cryptanalysis of substitution ciphers[J]. Cryptologia, 1995,Vol.19(3): 265-274.

[5] Jones, Michael N.. Queen’s University, Kingston,et al. Case-sensitive letter and bigram frequency counts from large-scale English corpora[J]. Behavior Research Methods, Instruments, & Computers,2004,Vol.36(3): 388-396.

[古典密码] 单表替换密码

http://dstbp.com/2025/07/30/msc/

作者

DSTBP

发布于

2025-07-30

更新于

2025-08-09

许可协议

CC BY 4.0

#

喜欢这篇文章？打赏一下作者吧

评论

GitHub
微信二维码

归档

最新文章

最新评论

×