发表更新密码学 / 日常训练5 小时读完 (大约44729个字)  次访问

[日常训练] Crypto Training - BUUCTF（一）

序言

本系列为博主在日常训练中对网上各大平台密码学题目的个人题解，题解不介绍具体知识点，不保证最优解法，仅供参考。这一期内容涵盖 BUUCTF 平台训练场中的 Crypto 类别题目，按解题数量从高到低排序，收录了前 1 至 100 道题的解题思路与过程，并根据涉及的密码学知识点进行分类整理。结合个人理解，将密码学类题目按考查重点划分为以下八类：

  • 编码与混淆（Encoding & Obfuscation）

    虽不属于严格意义上的“加密”，但在密码题中常作为基础步骤出现。典型形式包括：

    • 各类标准编码（Base64、URL 编码）
    • 进制转换（二进制、八进制、十六进制等）
    • 字符串混淆（兽音译者、JSFuck）
    • 简单扰动（XOR 操作、位反转）

  • 传统古典密码（Classical Cryptography）

    早期古典密码技术，核心考点为替换与移位机制，常考察手工破解能力。典型形式包括：

    • 单表替换（凯撒密码）
    • 多表替换（维吉尼亚密码）
    • 图形替换（猪圈密码、摩斯电码）
    • 换位加密（栅栏密码）
    • 混合密码（恩尼格玛机）

  • 现代对称密码（Symmetric Cryptography）

    考察现代加密算法实现或使用方式，常涉及密钥管理和模式漏洞。典型形式包括：

    • 分组加密（AES、DES）
    • 流加密（RC4、Rabbit）
    • 模式漏洞（ECB 信息泄露）
    • 填充攻击（Padding Oracle）

  • 现代非对称密码（Asymmetric Cryptography）

    以 RSA 为代表的公钥密码系统为核心，考察其数学原理与实际应用中的安全隐患。典型形式包括：

    • 数学构造型密码（RSA、ECC）
    • 参数不安全型（共模攻击、低加密指数攻击）
    • 结构缺陷型（Håstad 攻击、CRT 重组）
    • 签名验证漏洞（Bleichenbacher 攻击）

  • 哈希与消息认证（Hash / MAC）

    涉及哈希函数特性或相关攻击技术。典型形式包括：

    • 哈希计算（MD5、SHA1）
    • 碰撞攻击（生日攻击）
    • 长度扩展攻击（Merkle-Damgård 构造漏洞）
    • 爆破攻击（彩虹表）

  • 应用密码学（Applied Cryptography）

    更贴近真实场景，重点在于加密协议、密钥管理以及实现漏洞。典型形式包括：

    • 参数设计漏洞（Nonce 重用）
    • 协议缺陷（TLS/SSL 中间人攻击）
    • 物理攻击（侧信道分析、电磁泄露）

  • 自定义构造题（Custom Crypto）

    该类题目不依赖标准加密算法，通常由出题者自定义加密逻辑，或将多种密码学知识点巧妙（并非巧妙）融合。需对题目进行逆向与逻辑分析。典型形式包括：

    • 算法构造型（结合数据结构与算法、原创加密流程、状态机等）
    • 数学建模型（运用数论等基础数学知识构造陷阱）
    • 混合型（多种加密知识点融合）

  • 信息隐藏与隐写术（Steganography）

    常与 Forensics 交叉， 虽不属于密码学的主流分类，但经常涉及。主要包括图片隐写、音频隐写、文件格式伪装、Zlib/Gzip 压缩混淆。

1. 编码与混淆

1.1 一眼就解密

1.1.1 题目

1
下面的字符串解密后便能获得flag：ZmxhZ3tUSEVfRkxBR19PRl9USElTX1NUUklOR30=

1.1.2 解题思路

Base64 编码

1.1.3 解题脚本

1
2
3
4
5
import base64

print(base64.b64decode('ZmxhZ3tUSEVfRkxBR19PRl9USElTX1NUUklOR30='))

# b'flag{THE_FLAG_OF_THIS_STRING}'

1.2 Url编码

1.2.1 题目

1
%66%6c%61%67%7b%61%6e%64%20%31%3d%31%7d

1.2.2 解题思路

Url 编码

1.2.3 解题脚本

1
2
3
4
5
6
7
from urllib import parse

encoded_text = '%66%6c%61%67%7b%61%6e%64%20%31%3d%31%7d'
decoded_text = parse.unquote(encoded_text)
print(decoded_text)

# flag{and 1=1}

1.3 Quoted-printable

1.3.1 题目

1
=E9=82=A3=E4=BD=A0=E4=B9=9F=E5=BE=88=E6=A3=92=E5=93=A6

1.3.2 解题思路

Quoted-printable 编码：使用可打印的 ASCII 字符表示各种编码格式下的字符。它属于 MIME 标准的一部分，常用于电子邮件、HTTP 头信息等场景。

1.3.3 解题脚本

1
2
3
4
5
6
7
8
import quopri

if __name__ == "__main__":
    ct = "=E9=82=A3=E4=BD=A0=E4=B9=9F=E5=BE=88=E6=A3=92=E5=93=A6"
    decoded = quopri.decodestring(ct)
    print(decoded.decode("utf8"))

    # flag{那你也很棒哦}

1.4 信息化时代的步伐

1.4.1 题目

1
2
3
# 也许中国可以早早进入信息化时代，但是被清政府拒绝了。附件中是数十年后一位伟人说的话的密文。请翻译出明文(答案为一串中文！)

606046152623600817831216121621196386

1.4.2 解题思路

中文电码（标准中文电码、中文电报码或中文电报明码），最早将汉字转换为电子信号的一种编码方式，用于电报传输中文信息。

最早的汉字电码由威基杰（S.A. Viguer）编制，他借鉴《康熙字典》的部首分类方式，从中挑选 6800 多个常用汉字，编成《电报新书》。随后郑观应将其改编为《中国电报新编》，成为中国最早的汉字电码本。

中文电码表采用四位阿拉伯数字（0001 到 9999）为编码，用于表示最多一万个汉字、字母和符号。汉字按部首优先、笔画次之的顺序排列，字母和符号则被放置在电码表的末尾。

1.4.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import requests
from lxml import etree

# 请求参数和头部
headers = {
    'Accept-Language': 'zh-CN,zh;q=0.9,en;q=0.8,en-GB;q=0.7,en-US;q=0.6',
    'Referer': 'http://code.mcdvisa.com/',
    'User-Agent': 'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/136.0.0.0 Safari/537.36 Edg/136.0.0.0',
}

params = (
    ('action', 'getcode'),
    ('i', '1'),
    ('w', '606046152623600817831216121621196386'),
)

# 发送请求获取HTML内容
response = requests.get('http://code.mcdvisa.com/save.php', headers=headers, params=params, verify=False)
response.encoding = 'utf-8'
root = etree.HTML(response.text)

# 转换为字典
result_dict = {}
for item in root.xpath('//ul/li/text()'):
    if '：' in item:
        code, char = item.split('：', 1)
        result_dict[code] = char

print(result_dict)
data = ''.join(result_dict.values())
print(f'flag{{{data}}}')

# flag{计算机要从娃抓起}

1.5 Unencode

1.5.1 题目

1
89FQA9WMD<V1A<V1S83DY.#<W3$Q,2TM]

1.5.2 解题思路

UUencode 编码：Unix 系统下用于通过 uucp 邮件系统传输二进制数据的一种编码格式。

1.5.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class UUencodeCipher:
    @staticmethod
    def uuencode(data):
        # 将所有字符转换为8位二进制并拼接
        bin_str = ''.join(format(ord(c), '08b') for c in data)

        # 补齐长度为24的倍数
        bin_str += '0' * ((24 - len(bin_str) % 24) % 24)

        # 添加长度字符（字节数）
        encoded = chr(32 + len(data))

        # 每6位转换为字符
        for i in range(0, len(bin_str), 6):
            val = int(bin_str[i:i+6], 2)
            encoded += chr(0x60 if val == 0 else val + 32)
        return encoded

    @staticmethod
    def uudecode(data):
        # 去除长度字符，解码为二进制字符串
        bin_str = ''.join(format(0 if c == '`' else ord(c) - 32, '06b') for c in data[1:])

        # 每8位转换为原始字符
        decoded = ''.join(chr(int(bin_str[i:i+8], 2)) for i in range(0, len(bin_str), 8))
        return decoded
    

if __name__ == "__main__":
    ciphertext = "89FQA9WMD<V1A<V1S83DY.#<W3$Q,2TM]"
    print(UUencodeCipher.uudecode(ciphertext))
    
    # flag{dsdasdsa99877LLLKK}

1.6 异性相吸

1.6.1 题目

1
2
3
4
5
6
7
# key.txt
asadsasdasdasdasdasdasdasdasdasdqwesqf

# 密文.txt
07 1F 00 03 08 04 12 55 03 10 54 58 4B 5C 58 4A
56 53 44 52 03 44 02 58 46 06 54 47 05 56 47 57
44 12 5D 4A 14 1B

1.6.2 解题思路

异或

1.6.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from Crypto.Util.number import bytes_to_long
from binascii import unhexlify


if __name__ == '__main__':
    with open("key.txt", "rb") as f:
        file1 = bytes_to_long(f.read())
    with open("密文.txt", "rb") as f:
        file2 = bytes_to_long(f.read())

    res = file1 ^ file2
    print(unhexlify(hex(res)[2:]))

    # flag{ea1bc0988992276b7f95b54a7435e89e}

1.7 密码学的心声

1.7.1 题目

1
二战时期，某国军官与一个音乐家情妇相好，然而自从那时起，他屡战屡败，敌人似乎料事如神。他也有怀疑过他的情妇，但是他经过24小时观察他的情妇，发现她每天都只是作曲，然后弹奏给战地电台，为士兵们鼓气，并未有任何逾越。那么，间谍到底是谁？这张曲谱是否有猫腻？ (答案为一个明文字符串，提交获得的有意义语句通顺字符串即可)

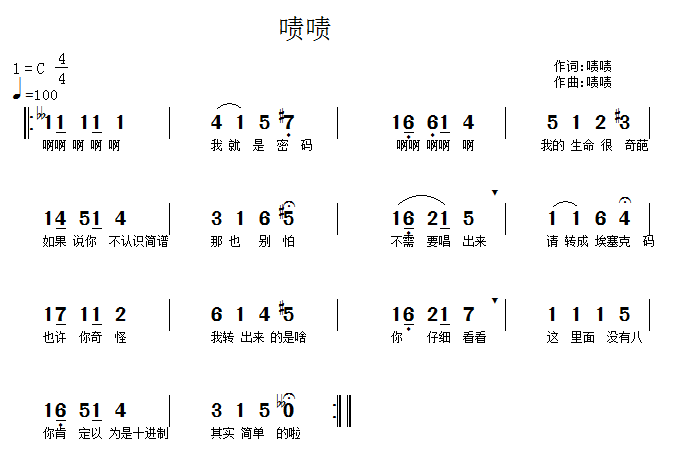
1.7.2 解题思路

进制转换：八进制数字三个一组转换为 ASCII 码

1.7.3 解题脚本

1
2
3
4
5
6
7
if __name__ == "__main__":
    ct = '111 114 157 166 145 123 145 143 165 162 151 164 171 126 145 162 171 115 165 143 150'
    # 八进制数转换为字符
    cipher = ''.join(chr(int(octal, 8)) for octal in ct.split())
    print(f"flag{{{cipher}}}")

    # flag{ILoveSecurityVeryMuch}

1.8 [BJDCTF2020]这是base??

1.8.1 题目

1
2
3
4
dict:{0: 'J', 1: 'K', 2: 'L', 3: 'M', 4: 'N', 5: 'O', 6: 'x', 7: 'y', 8: 'U', 9: 'V', 10: 'z', 11: 'A', 12: 'B', 13: 'C', 14: 'D', 15: 'E', 16: 'F', 17: 'G', 18: 'H', 19: '7', 20: '8', 21: '9', 22: 'P', 23: 'Q', 24: 'I', 25: 'a', 26: 'b', 27: 'c', 28: 'd', 29: 'e', 30: 'f', 31: 'g', 32: 'h', 33: 'i', 34: 'j', 35: 'k', 36: 'l', 37: 'm', 38: 'W', 39: 'X', 40: 'Y', 41: 'Z', 42: '0', 43: '1', 44: '2', 45: '3', 46: '4', 47: '5', 48: '6', 49: 'R', 50: 'S', 51: 'T', 52: 'n', 53: 'o', 54: 'p', 55: 'q', 56: 'r', 57: 's', 58: 't', 59: 'u', 60: 'v', 61: 'w', 62: '+', 63: '/', 64: '='}

chipertext:
FlZNfnF6Qol6e9w17WwQQoGYBQCgIkGTa9w3IQKw

1.8.2 解题思路

自定义码表 Base64

1.8.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
import base64
from typing import Optional

class BaseXEncoder:
    # 常见进制的编码表
    STANDARD_TABLES = {
        16: b"0123456789ABCDEF",
        32: b"ABCDEFGHIJKLMNOPQRSTUVWXYZ234567",
        58: b"123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz",
        62: b"0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz",
        64: b"ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/",
        91: b"ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789!#$%&()*+,./:;<=>?@[]^_`{|}~\"",
        92: b"!\"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\\]^_`abcdefghijklmnopqrstuvwxyz{|}~",
        128: bytes(range(128)),  # 每个字节本身
    }

    def encode(self, data: bytes, base: int, table: Optional[bytes] = None, padding: Optional[bytes] = b"=") -> str:
        """
        编码函数：支持 base16, base32, base64, base58, base62, base91, base92, base128
        """
        table = table or self.STANDARD_TABLES.get(base)

        # 标准 base 编码（内置支持填充）
        if base == 16:
            encoded = base64.b16encode(data).translate(bytes.maketrans(b"0123456789ABCDEF", table))
        elif base == 32:
            encoded = base64.b32encode(data).translate(bytes.maketrans(self.STANDARD_TABLES[32], table))
        elif base == 64:
            encoded = base64.b64encode(data).translate(bytes.maketrans(self.STANDARD_TABLES[64], table))
        elif base in (58, 62, 91, 92, 128):  # 自定义 baseX 编码
            return self._baseX_encode(data, table).decode("utf8")
        else:
            raise ValueError(f"Unsupported base: {base}")

        # 处理填充字符
        if padding is None:
            encoded = encoded.rstrip(b"=")
        elif padding != b"=":
            encoded = encoded.rstrip(b"=").replace(b"=", padding)

        return encoded.decode("utf8")

    def decode(self, ciphertext: str, base: int, table: Optional[bytes] = None, padding: Optional[bytes] = b"=") -> bytes:
        """
        解码函数：对应 encode 函数的逆过程
        """
        encoded = ciphertext.encode("utf-8")
        table = table or self.STANDARD_TABLES.get(base)

        if base in (58, 62, 91, 92, 128):
            return self._baseX_decode(encoded, table)

        # 恢复 padding
        if padding is not None and padding != b"=":
            encoded = encoded.replace(padding, b"=")

        # 计算并自动补足 base32/base64 所需的 padding 长度
        def pad_base(data: bytes, block_size: int = 8) -> bytes:
            pad_len = (-len(data)) % block_size
            return data + b'=' * pad_len

        if base == 16:
            return base64.b16decode(encoded.translate(bytes.maketrans(table, b"0123456789ABCDEF")))
        elif base == 32:
            padded = pad_base(encoded)  # base32 长度必须为 8 的倍数
            return base64.b32decode(padded.translate(bytes.maketrans(table, self.STANDARD_TABLES[32])))
        elif base == 64:
            padded = pad_base(encoded, block_size=4)  # base64 长度必须为 4 的倍数
            return base64.b64decode(padded.translate(bytes.maketrans(table, self.STANDARD_TABLES[64])))
        else:
            raise ValueError(f"Unsupported base: {base}")

    def _baseX_encode(self, data: bytes, table: bytes) -> bytes:
        """
        自定义 baseX 编码（如 base58/base62）：将字节数据按目标进制编码为字符表中的字符序列
        """
        num = int.from_bytes(data, byteorder='big')
        base = len(table)
        encoded = bytearray()

        while num > 0:
            num, rem = divmod(num, base)
            encoded.insert(0, table[rem])

        # 前导 0 用 table[0] 表示
        pad = 0
        for b in data:
            if b == 0:
                pad += 1
            else:
                break

        return bytes([table[0]]) * pad + bytes(encoded)

    def _baseX_decode(self, encoded: bytes, table: bytes) -> bytes:
        """
        自定义 baseX 解码：将字符序列转换回原始字节数据
        """
        base = len(table)
        index = {char: i for i, char in enumerate(table)}
        num = 0
        for char in encoded:
            num = num * base + index[char]

        decoded = num.to_bytes((num.bit_length() + 7) // 8, byteorder='big')

        # 处理前导 0
        pad = 0
        for c in encoded:
            if c == table[0]:
                pad += 1
            else:
                break

        return b'\x00' * pad + decoded


if __name__ == '__main__':
    encoder = BaseXEncoder()
    Codetable = {0: 'J', 1: 'K', 2: 'L', 3: 'M', 4: 'N', 5: 'O', 6: 'x', 7: 'y', 8: 'U', 9: 'V', 10: 'z', 11: 'A', 12: 'B', 13: 'C', 14: 'D', 15: 'E', 16: 'F', 17: 'G', 18: 'H', 19: '7', 20: '8', 21: '9', 22: 'P', 23: 'Q', 24: 'I', 25: 'a', 26: 'b', 27: 'c', 28: 'd', 29: 'e', 30: 'f', 31: 'g', 32: 'h', 33: 'i', 34: 'j', 35: 'k', 36: 'l', 37: 'm', 38: 'W', 39: 'X', 40: 'Y', 41: 'Z', 42: '0', 43: '1', 44: '2', 45: '3', 46: '4', 47: '5', 48: '6', 49: 'R', 50: 'S', 51: 'T', 52: 'n', 53: 'o', 54: 'p', 55: 'q', 56: 'r', 57: 's', 58: 't', 59: 'u', 60: 'v', 61: 'w', 62: '+', 63: '/', 64: '='}
    chipertext = "FlZNfnF6Qol6e9w17WwQQoGYBQCgIkGTa9w3IQKw"
    table = ''.join(Codetable[key] for key in Codetable).encode()
    flag = encoder.decode(chipertext, 64, table[:-1])
    print(flag)

    # b'BJD{D0_Y0u_kNoW_Th1s_b4se_map}'

1.9 这是什么

1.9.1 题目

1
2
3
4
# 题目描述
小明是一个软件专业的高材生，但是老师布置的这次的作业似乎不怎么靠谱，因为他们老师以前是学物理的！喜欢乱七八糟命名文件，还喜欢奇奇怪怪的编码。你快帮小明看一下这题，小明准备好了一箱子辣条。

[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]][([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+([][[]]+[])[+!+[]]+(![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[+!+[]]+([][[]]+[])[+[]]+([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+(!![]+[])[+!+[]]]((![]+[])[+!+[]]+(![]+[])[!+[]+!+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]+(!![]+[])[+[]]+(![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[!+[]+!+[]+[+[]]]+([]+[])[(![]+[])[+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+([][[]]+[])[+!+[]]+(!![]+[])[+[]]+([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+(!![]+[])[+!+[]]]()[+!+[]+[!+[]+!+[]]]+(![]+[])[+[]]+(![]+[])[!+[]+!+[]]+(![]+[])[+!+[]]+(+![]+[![]]+([]+[])[([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+([][[]]+[])[+!+[]]+(![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[+!+[]]+([][[]]+[])[+[]]+([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+(!![]+[])[+!+[]]])[!+[]+!+[]+[+[]]]+(+[![]]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[!+[]+!+[]+[+!+[]]]+(![]+[])[+!+[]]+[+[]]+[!+[]+!+[]+!+[]+!+[]]+[!+[]+!+[]+!+[]+!+[]]+[!+[]+!+[]+!+[]+!+[]+!+[]+!+[]+!+[]+!+[]]+(![]+[])[+[]]+([][[]]+[])[!+[]+!+[]]+[!+[]+!+[]+!+[]+!+[]+!+[]+!+[]+!+[]]+[!+[]+!+[]+!+[]]+[+[]]+(+(+!+[]+[+!+[]]))[(!![]+[])[+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+(+![]+([]+[])[([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+([][[]]+[])[+!+[]]+(![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[+!+[]]+([][[]]+[])[+[]]+([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+(!![]+[])[+[]]+(!![]+[])[+!+[]]+([![]]+[][[]])[+!+[]+[+[]]]+([][[]]+[])[+!+[]]+(+![]+[![]]+([]+[])[([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+([][[]]+[])[+!+[]]+(![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[+!+[]]+([][[]]+[])[+[]]+([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+(!![]+[])[+!+[]]])[!+[]+!+[]+[+[]]]](!+[]+!+[]+[+[]])+[!+[]+!+[]+!+[]+!+[]+!+[]+!+[]]+[!+[]+!+[]]+([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+[+!+[]]+[!+[]+!+[]+!+[]]+([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(![]+[])[+!+[]]+[!+[]+!+[]+!+[]+!+[]+!+[]+!+[]+!+[]+!+[]]+[+[]]+[!+[]+!+[]]+[+[]]+[+[]]+([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+[!+[]+!+[]+!+[]+!+[]]+[!+[]+!+[]+!+[]+!+[]+!+[]]+[!+[]+!+[]]+[!+[]+!+[]+!+[]+!+[]+!+[]+!+[]+!+[]+!+[]+!+[]]+([][[]]+[])[!+[]+!+[]]+(![]+[])[+!+[]]+(![]+[])[+!+[]]+[!+[]+!+[]]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]][([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+([][[]]+[])[+!+[]]+(![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[+!+[]]+([][[]]+[])[+[]]+([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+(!![]+[])[+!+[]]]((!![]+[])[+!+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+([][[]]+[])[+[]]+(!![]+[])[+!+[]]+([][[]]+[])[+!+[]]+(+[![]]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+!+[]]]+([][[]]+[])[+[]]+([][[]]+[])[+!+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(![]+[])[!+[]+!+[]+!+[]]+([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(![]+[])[+!+[]]+(+(!+[]+!+[]+[+!+[]]+[+!+[]]))[(!![]+[])[+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+(+![]+([]+[])[([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+([][[]]+[])[+!+[]]+(![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[+!+[]]+([][[]]+[])[+[]]+([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+(!![]+[])[+[]]+(!![]+[])[+!+[]]+([![]]+[][[]])[+!+[]+[+[]]]+([][[]]+[])[+!+[]]+(+![]+[![]]+([]+[])[([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+([][[]]+[])[+!+[]]+(![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[+!+[]]+([][[]]+[])[+[]]+([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+(!![]+[])[+!+[]]])[!+[]+!+[]+[+[]]]](!+[]+!+[]+!+[]+[+!+[]])[+!+[]]+(!![]+[])[!+[]+!+[]+!+[]])()([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]][([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+([][[]]+[])[+!+[]]+(![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[+!+[]]+([][[]]+[])[+[]]+([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+(!![]+[])[+!+[]]]((!![]+[])[+!+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+([][[]]+[])[+[]]+(!![]+[])[+!+[]]+([][[]]+[])[+!+[]]+(+[![]]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+!+[]]]+(!![]+[])[!+[]+!+[]+!+[]]+(![]+[])[!+[]+!+[]+!+[]]+([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(![]+[])[+!+[]]+(+(!+[]+!+[]+[+!+[]]+[+!+[]]))[(!![]+[])[+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+(+![]+([]+[])[([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+([][[]]+[])[+!+[]]+(![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[+!+[]]+([][[]]+[])[+[]]+([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+(!![]+[])[+[]]+(!![]+[])[+!+[]]+([![]]+[][[]])[+!+[]+[+[]]]+([][[]]+[])[+!+[]]+(+![]+[![]]+([]+[])[([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+([][[]]+[])[+!+[]]+(![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[+!+[]]+([][[]]+[])[+[]]+([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+(!![]+[])[+!+[]]])[!+[]+!+[]+[+[]]]](!+[]+!+[]+!+[]+[+!+[]])[+!+[]]+(!![]+[])[!+[]+!+[]+!+[]])()(([]+[])[([![]]+[][[]])[+!+[]+[+[]]]+(!![]+[])[+[]]+(![]+[])[+!+[]]+(![]+[])[!+[]+!+[]]+([![]]+[][[]])[+!+[]+[+[]]]+([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(![]+[])[!+[]+!+[]+!+[]]]()[+[]])[+[]]+[!+[]+!+[]+!+[]+!+[]+!+[]+!+[]+!+[]]+([][[]]+[])[!+[]+!+[]])+([]+[])[(![]+[])[+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+([][[]]+[])[+!+[]]+(!![]+[])[+[]]+([][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]]+[])[!+[]+!+[]+!+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[+!+[]+[+[]]]+(!![]+[])[+!+[]]]()[+!+[]+[!+[]+!+[]]]+(!![]+[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]]+(![]+[])[!+[]+!+[]]+(!![]+[])[+[]]+(!![]+[])[!+[]+!+[]+!+[]]+(!![]+[])[+!+[]]])[!+[]+!+[]+[+[]]])()

1.9.2 解题思路

文件后缀伪造（docx → apk）

JSfuck 前端混淆

1.9.3 解题脚本

1
2
3
4
5
6
7
8
from unjsfuck import unjsfuck

if __name__ == '__main__':
    ct = '[][(![]+[])[+[]]+([![]]+[][[]])[+!+[]+[+[]]....'
    pt = unjsfuck(ct)
    print(pt)

    # []['filter']['constructor']('alert("flag{a0448fd730b62c13ca80200c4529daa2}")')()

1.10 [BJDCTF2020]signin

1.10.1 题目

1
2
welcome to crypto world！！
密文：424a447b57653163306d655f74345f424a444354467d

1.10.2 解题思路

hex 编码

1.10.3 解题脚本

1
2
3
4
5
6
from Crypto.Util.number import long_to_bytes

if __name__ == "__main__":
    print(long_to_bytes(0x424a447b57653163306d655f74345f424a444354467d))

    # b'BJD{We1c0me_t4_BJDCTF}'

1.11 传感器

1.11.1 题目

1
2
3
4
5
6
5555555595555A65556AA696AA6666666955
这是某压力传感器无线数据包解调后但未解码的报文(hex)
  
已知其ID为0xFED31F，请继续将报文完整解码，提交hex。

提示1：曼联

1.11.2 解题思路

802.3 曼彻斯特编码（逆序） + 进制转换

1.11.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
def convert_base(num_str: str, from_base: int, to_base: int, zfill: int = 0) -> str:
    """
    通用进制转换函数，支持填充位数
    """
    if not (2 <= from_base <= 36 and 2 <= to_base <= 36):
        raise ValueError("进制必须在 2 到 36 之间")

    digits = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"

    # 将输入字符串转换为10进制整数
    num_str = num_str.strip().upper()
    num = 0
    for char in num_str:
        val = digits.find(char)
        if val == -1 or val >= from_base:
            raise ValueError(f"非法字符 '{char}' 对于进制 {from_base}")
        num = num * from_base + val

    # 特殊情况：输入为 0
    if num == 0:
        return "0".zfill(zfill)

    # 转换为目标进制
    result = ""
    while num > 0:
        result = digits[num % to_base] + result
        num //= to_base

    return result.zfill(zfill)


class ManchesterDecoder:
    @staticmethod
    def byteinvert(str_bin):
        # 字节内位反转（8位为一组）
        ret = ''
        for i in range(len(str_bin) // 8):
            ret += str_bin[i*8:i*8+8][::-1]
        return ret

    # ---------- 解码函数 ----------

    @staticmethod
    def MCST_stand_decode(str_bin, isinvert=False):
        # 标准曼彻斯特解码（Standard Manchester Encoding）
        # 规则：0 -> 01，1 -> 10
        ret = ''
        for i in range(len(str_bin) // 2):
            x = str_bin[i*2:i*2+2]
            if x == '01':
                ret += '0'
            elif x == '10':
                ret += '1'
            else:
                return '标准曼彻斯特解码错误！'
        if isinvert:
            return ManchesterDecoder.byteinvert(ret)
        else:
            return ret

    @staticmethod
    def MCST_IEEE_decode(str_bin, isinvert=False):
        # IEEE 802.3 曼彻斯特解码（逻辑与标准相反）
        # 规则：0 -> 10，1 -> 01
        ret = ''
        for i in range(len(str_bin) // 2):
            x = str_bin[i*2:i*2+2]
            if x == '01':
                ret += '1'
            elif x == '10':
                ret += '0'
            else:
                return 'IEEE曼彻斯特解码错误！'
        if isinvert:
            return ManchesterDecoder.byteinvert(ret)
        else:
            return ret

    @staticmethod
    def MCST_diff_decode(str_bin, isinvert=False):
        # 差分曼彻斯特编码（Differential Manchester Encoding）解码
        # 解码逻辑：两段编码相同表示0，不同表示1
        ret = ''
        for i in range(0, len(str_bin) // 2 - 1):
            x1 = str_bin[i*2:i*2+2]
            x2 = str_bin[i*2+2:i*2+4]
            if x1 == x2:
                ret += '0'
            else:
                ret += '1'
        if isinvert:
            return ManchesterDecoder.byteinvert(ret)
        else:
            return ret

    # ---------- 编码函数 ----------

    @staticmethod
    def MCST_stand_encode(bit_str, isinvert=False):
        # 标准曼彻斯特编码
        # 0 -> 01，1 -> 10
        if isinvert:
            bit_str = ManchesterDecoder.byteinvert(bit_str)
        ret = ''
        for bit in bit_str:
            if bit == '0':
                ret += '01'
            elif bit == '1':
                ret += '10'
            else:
                raise ValueError('输入必须是二进制字符串')
        return ret

    @staticmethod
    def MCST_IEEE_encode(bit_str, isinvert=False):
        # IEEE 802.3 曼彻斯特编码
        # 0 -> 10，1 -> 01
        if isinvert:
            bit_str = ManchesterDecoder.byteinvert(bit_str)
        ret = ''
        for bit in bit_str:
            if bit == '0':
                ret += '10'
            elif bit == '1':
                ret += '01'
            else:
                raise ValueError('输入必须是二进制字符串')
        return ret

    @staticmethod
    def MCST_diff_encode(bit_str, isinvert=False):
        # 差分曼彻斯特编码
        # 差分曼彻斯特编码以一个初始状态开始，0表示保持前半周期电平不变，1表示反转
        # 这里用'01'和'10'代表两种状态，初始状态为'01'
        if isinvert:
            bit_str = ManchesterDecoder.byteinvert(bit_str)
        ret = ''
        prev = '0'  # 假设初始电平为0，对应编码'01'
        for bit in bit_str:
            if bit == '0':
                # 0表示信号电平保持不变，编码为与上一个一样
                if prev == '0':
                    ret += '01'
                else:
                    ret += '10'
            elif bit == '1':
                # 1表示电平反转，编码为与上一个相反
                if prev == '0':
                    ret += '10'
                    prev = '1'
                else:
                    ret += '01'
                    prev = '0'
            else:
                raise ValueError('输入必须是二进制字符串')
        return ret


if __name__ == '__main__':
    ct = "5555555595555A65556AA696AA6666666955"
    ct = convert_base(ct, 16, 2, len(ct)*4)

    result = ManchesterDecoder.MCST_IEEE_decode(ct, True)
    print(f'flag{{{convert_base(result, 2, 16)}}}')

    # flag{FFFFFED31F645055F9}

1.12 yxx

1.12.1 题目

1
2
3
4
5
6
# 明文.txt
lovelovelovelovelovelovelovelove

# 密文.txt
0A 03 17 02 56 01 15 11 0A 14 0E 0A 1E 30 0E 0A
1E 30 0E 0A 1E 30 14 0C 19 0D 1F 10 0E 06 03 18

1.12.2 解题思路

异或

1.12.3 解题脚本

1
2
3
4
5
6
7
8
9
if __name__ == "__main__":
    pt = b'lovelovelovelovelovelovelovelove'
    with open("yxx/密文.txt", "rb") as f:
        ct = f.read()

    result = bytes([c ^ pt[i % len(pt)] for i, c in enumerate(ct)])
    print(result.decode('utf-8'))

    # flag:nctf{xor_xor_xor_biubiubiu}

1.13 [WUSTCTF2020]B@se

1.13.1 题目

1
2
3
4
瀵嗘枃锛歁yLkTaP3FaA7KOWjTmKkVjWjVzKjdeNvTnAjoH9iZOIvTeHbvD==
JASGBWcQPRXEFLbCDIlmnHUVKTYZdMovwipatNOefghq56rs****kxyz012789+/

oh holy shit, something is missing...

1.13.2 解题思路

爆破码表 + 自定义码表 Base64

1.13.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
import base64
from typing import Optional
from itertools import permutations


class BaseXEncoder:
    # 常见进制的编码表
    STANDARD_TABLES = {
        16: b"0123456789ABCDEF",
        32: b"ABCDEFGHIJKLMNOPQRSTUVWXYZ234567",
        58: b"123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz",
        62: b"0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz",
        64: b"ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/",
        91: b"ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789!#$%&()*+,./:;<=>?@[]^_`{|}~\"",
        92: b"!\"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\\]^_`abcdefghijklmnopqrstuvwxyz{|}~",
        128: bytes(range(128)),  # 每个字节本身
    }

    def encode(self, data: bytes, base: int, table: Optional[bytes] = None, padding: Optional[bytes] = b"=") -> str:
        """
        编码函数：支持 base16, base32, base64, base58, base62, base91, base92, base128
        """
        table = table or self.STANDARD_TABLES.get(base)

        # 标准 base 编码（内置支持填充）
        if base == 16:
            encoded = base64.b16encode(data).translate(bytes.maketrans(b"0123456789ABCDEF", table))
        elif base == 32:
            encoded = base64.b32encode(data).translate(bytes.maketrans(self.STANDARD_TABLES[32], table))
        elif base == 64:
            encoded = base64.b64encode(data).translate(bytes.maketrans(self.STANDARD_TABLES[64], table))
        elif base in (58, 62, 91, 92, 128):  # 自定义 baseX 编码
            return self._baseX_encode(data, table).decode("utf8")
        else:
            raise ValueError(f"Unsupported base: {base}")

        # 处理填充字符
        if padding is None:
            encoded = encoded.rstrip(b"=")
        elif padding != b"=":
            encoded = encoded.rstrip(b"=").replace(b"=", padding)

        return encoded.decode("utf8")

    def decode(self, ciphertext: str, base: int, table: Optional[bytes] = None, padding: Optional[bytes] = b"=") -> bytes:
        """
        解码函数：对应 encode 函数的逆过程
        """
        encoded = ciphertext.encode("utf-8")
        table = table or self.STANDARD_TABLES.get(base)

        if base in (58, 62, 91, 92, 128):
            return self._baseX_decode(encoded, table)

        # 恢复 padding
        if padding is not None and padding != b"=":
            encoded = encoded.replace(padding, b"=")

        # 计算并自动补足 base32/base64 所需的 padding 长度
        def pad_base(data: bytes, block_size: int = 8) -> bytes:
            pad_len = (-len(data)) % block_size
            return data + b'=' * pad_len

        if base == 16:
            return base64.b16decode(encoded.translate(bytes.maketrans(table, b"0123456789ABCDEF")))
        elif base == 32:
            padded = pad_base(encoded)  # base32 长度必须为 8 的倍数
            return base64.b32decode(padded.translate(bytes.maketrans(table, self.STANDARD_TABLES[32])))
        elif base == 64:
            padded = pad_base(encoded, block_size=4)  # base64 长度必须为 4 的倍数
            return base64.b64decode(padded.translate(bytes.maketrans(table, self.STANDARD_TABLES[64])))
        else:
            raise ValueError(f"Unsupported base: {base}")

    def _baseX_encode(self, data: bytes, table: bytes) -> bytes:
        """
        自定义 baseX 编码（如 base58/base62）：将字节数据按目标进制编码为字符表中的字符序列
        """
        num = int.from_bytes(data, byteorder='big')
        base = len(table)
        encoded = bytearray()

        while num > 0:
            num, rem = divmod(num, base)
            encoded.insert(0, table[rem])

        # 前导 0 用 table[0] 表示
        pad = 0
        for b in data:
            if b == 0:
                pad += 1
            else:
                break

        return bytes([table[0]]) * pad + bytes(encoded)

    def _baseX_decode(self, encoded: bytes, table: bytes) -> bytes:
        """
        自定义 baseX 解码：将字符序列转换回原始字节数据
        """
        base = len(table)
        index = {char: i for i, char in enumerate(table)}
        num = 0
        for char in encoded:
            num = num * base + index[char]

        decoded = num.to_bytes((num.bit_length() + 7) // 8, byteorder='big')

        # 处理前导 0
        pad = 0
        for c in encoded:
            if c == table[0]:
                pad += 1
            else:
                break

        return b'\x00' * pad + decoded


if __name__ == '__main__':
    encoder = BaseXEncoder()
    STANDARD_ALPHABET = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/'
    custom_alphabet = "JASGBWcQPRXEFLbCDIlmnHUVKTYZdMovwipatNOefghq56rs****kxyz012789+/"
    diff_lst = [c for c in set(STANDARD_ALPHABET) - set(custom_alphabet)]
    combos = permutations(diff_lst, 4)

    # 爆破 ****
    for combo in combos:
        table = custom_alphabet.replace('****', ''.join(combo))
        ct = 'MyLkTaP3FaA7KOWjTmKkVjWjVzKjdeNvTnAjoH9iZOIvTeHbvD=='
        flag = BaseXEncoder().decode(ct, 64, table.encode())

        if b'wctf2020' in flag:
            print(flag)

            # wctf2020{base64_1s_v3ry_e@sy_and_fuN}

1.14 [AFCTF2018]BASE

1.14.1 题目

附件： attachment.zip

1.14.2 解题思路

十六进制 + base64 + base32 + base16

1.14.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
import base64
from typing import Optional


class BaseXEncoder:
    # 常见进制的编码表
    STANDARD_TABLES = {
        16: b"0123456789ABCDEF",
        32: b"ABCDEFGHIJKLMNOPQRSTUVWXYZ234567",
        58: b"123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz",
        62: b"0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz",
        64: b"ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/",
        91: b"ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789!#$%&()*+,./:;<=>?@[]^_`{|}~\"",
        92: b"!\"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\\]^_`abcdefghijklmnopqrstuvwxyz{|}~",
        128: bytes(range(128)),  # 每个字节本身
    }

    def encode(self, data: bytes, base: int, table: Optional[bytes] = None, padding: Optional[bytes] = b"=") -> str:
        """
        编码函数：支持 base16, base32, base64, base58, base62, base91, base92, base128
        """
        table = table or self.STANDARD_TABLES.get(base)

        # 标准 base 编码（内置支持填充）
        if base == 16:
            encoded = base64.b16encode(data).translate(bytes.maketrans(b"0123456789ABCDEF", table))
        elif base == 32:
            encoded = base64.b32encode(data).translate(bytes.maketrans(self.STANDARD_TABLES[32], table))
        elif base == 64:
            encoded = base64.b64encode(data).translate(bytes.maketrans(self.STANDARD_TABLES[64], table))
        elif base in (58, 62, 91, 92, 128):  # 自定义 baseX 编码
            return self._baseX_encode(data, table).decode("utf8")
        else:
            raise ValueError(f"Unsupported base: {base}")

        # 处理填充字符
        if padding is None:
            encoded = encoded.rstrip(b"=")
        elif padding != b"=":
            encoded = encoded.rstrip(b"=").replace(b"=", padding)

        return encoded.decode("utf8")

    def decode(self, ciphertext: str, base: int, table: Optional[bytes] = None, padding: Optional[bytes] = b"=") -> bytes:
        """
        解码函数：对应 encode 函数的逆过程
        """
        encoded = ciphertext.encode("utf-8")
        table = table or self.STANDARD_TABLES.get(base)

        if base in (58, 62, 91, 92, 128):
            return self._baseX_decode(encoded, table)

        # 恢复 padding
        if padding is not None and padding != b"=":
            encoded = encoded.replace(padding, b"=")

        # 计算并自动补足 base32/base64 所需的 padding 长度
        def pad_base(data: bytes, block_size: int = 8) -> bytes:
            pad_len = (-len(data)) % block_size
            return data + b'=' * pad_len

        if base == 16:
            return base64.b16decode(encoded.translate(bytes.maketrans(table, b"0123456789ABCDEF")))
        elif base == 32:
            padded = pad_base(encoded)  # base32 长度必须为 8 的倍数
            return base64.b32decode(padded.translate(bytes.maketrans(table, self.STANDARD_TABLES[32])))
        elif base == 64:
            padded = pad_base(encoded, block_size=4)  # base64 长度必须为 4 的倍数
            return base64.b64decode(padded.translate(bytes.maketrans(table, self.STANDARD_TABLES[64])))
        else:
            raise ValueError(f"Unsupported base: {base}")

    def _baseX_encode(self, data: bytes, table: bytes) -> bytes:
        """
        自定义 baseX 编码（如 base58/base62）：将字节数据按目标进制编码为字符表中的字符序列
        """
        num = int.from_bytes(data, byteorder='big')
        base = len(table)
        encoded = bytearray()

        while num > 0:
            num, rem = divmod(num, base)
            encoded.insert(0, table[rem])

        # 前导 0 用 table[0] 表示
        pad = 0
        for b in data:
            if b == 0:
                pad += 1
            else:
                break

        return bytes([table[0]]) * pad + bytes(encoded)

    def _baseX_decode(self, encoded: bytes, table: bytes) -> bytes:
        """
        自定义 baseX 解码：将字符序列转换回原始字节数据
        """
        base = len(table)
        index = {char: i for i, char in enumerate(table)}
        num = 0
        for char in encoded:
            num = num * base + index[char]

        decoded = num.to_bytes((num.bit_length() + 7) // 8, byteorder='big')

        # 处理前导 0
        pad = 0
        for c in encoded:
            if c == table[0]:
                pad += 1
            else:
                break

        return b'\x00' * pad + decoded


if __name__ == '__main__':
    encoder = BaseXEncoder()
    with open(r"flag_encode.txt", 'r') as f:
        ct = f.read()
    ct = bytes.fromhex(ct).decode("utf8")
    while True:
        try:
            ct = encoder.decode(ct, 64).decode("utf8")
        except Exception:
            try:
                ct = encoder.decode(ct, 32).decode("utf8")
            except Exception:
                ct = encoder.decode(ct, 16).decode("utf8")
        if 'afctf' in ct:
            print(ct)
            break

            # afctf{U_5h0u1d_Us3_T00l5}

1.15 鸡藕椒盐味

1.15.1 题目

1
公司食堂最新出了一种小吃，叫鸡藕椒盐味汉堡，售价八块钱，为了促销，上面有一个验证码，输入后可以再换取一个汉堡。但是问题是每个验证码几乎都有错误,而且打印的时候倒了一下。小明买到了一个汉堡，准备还原验证码，因为一个吃不饱啊验证码如下：1100 1010 0000 ,而且打印的时候倒了一下。把答案哈希一下就可以提交了。(答案为正确值(不包括数字之间的空格)的32位md5值的小写形式)

1.15.2 解题思路

海明校验码：每个汉堡 8 块表示数据位为 8 bits，校验位为 4 bits，并且校验位在 $ 2^n $ 的位置。

1.15.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
import hashlib
from typing import Union
from gmssl import sm3

class HammingCode:
    """海明码校验"""
    @staticmethod
    def _calculate_parity_bits(m):
        """计算所需的校验位数量"""
        r = 0
        while 2**r < m + r + 1:
            r += 1
        return r
    
    @staticmethod
    def _is_power_of_two(n):
        """判断是否为2的幂"""
        return n != 0 and (n & (n - 1)) == 0
    
    def encode(self, data_bits):
        """生成海明校验码"""
        data = [int(bit) for bit in str(data_bits)]
        m = len(data)
        r = self._calculate_parity_bits(m)
        
        # 初始化海明码，预留校验位位置
        hamming = [0] * (m + r)
        data_idx = 0
        
        # 填充数据位
        for i in range(1, m + r + 1):
            if not self._is_power_of_two(i):
                hamming[i-1] = data[data_idx]
                data_idx += 1
        
        # 计算校验位
        for i in range(r):
            pos = 2**i
            parity = 0
            for j in range(1, m + r + 1):
                if j & pos:
                    parity ^= hamming[j-1]
            hamming[pos-1] = parity
        
        return ''.join(map(str, hamming))
    
    def verify(self, hamming_code):
        """验证/纠错海明码"""
        received = [int(bit) for bit in str(hamming_code)]
        n = len(received)
        
        # 计算校验位数
        r = 0
        while 2**r < n:
            r += 1
        
        # 计算错误位置
        error_pos = 0
        for i in range(r):
            pos = 2**i
            parity = 0
            for j in range(1, n + 1):
                if j & pos:
                    parity ^= received[j-1]
            if parity != 0:
                error_pos += pos
        
        # 纠正错误
        corrected = received.copy()
        if error_pos != 0 and error_pos <= len(corrected):
            corrected[error_pos - 1] ^= 1
        
        # 提取原始数据
        original_data = []
        for i in range(1, n + 1):
            if not self._is_power_of_two(i):
                original_data.append(str(corrected[i-1]))
        
        return {
            'corrected_code': ''.join(map(str, corrected)),
            'error_position': error_pos,
            'original_data': ''.join(original_data)
        }


def hash_data(data: Union[bytes, str], algorithm: str, output_type: str = "hex", hash_length: int = None, hex_case: str = "lower") -> tuple:
    """
    计算数据的哈希值，支持多种算法和输出类型
    """
    # 统一转换为字节类型（兼容字符串输入）
    data_bytes = data.encode("utf-8") if isinstance(data, str) else data

    # 计算哈希值及长度
    match algorithm.lower():
        case "sha256" | "md5" | "sha1":
            hasher = hashlib.new(algorithm, data_bytes)
            digest = hasher.digest()
            original_length = hasher.digest_size

        case "sm3":
            hex_digest = sm3.sm3_hash(list(data_bytes))  # gmssl返回十六进制字符串
            digest = bytes.fromhex(hex_digest)           # 转换为字节
            original_length = 32                         # SM3固定32字节

        case _:
            raise ValueError(f"不支持的算法: {algorithm}（支持：sha256/md5/sha1/sm3）")

    # 长度控制
    if hash_length is not None:
        if not isinstance(hash_length, int) or hash_length <= 0:
            raise ValueError("hash_length必须是正整数")
        if hash_length > original_length:
            raise ValueError(f"长度超出限制（最大{original_length}字节）")
        digest = digest[:hash_length]  # 截断字节串
        actual_length = hash_length
    else:
        actual_length = original_length  # 不截断时使用原始长度

    # 转换输出类型
    match output_type.lower():
        case "bytes":
            result = digest
        case "hex":
            hex_str = digest.hex()
            # 十六进制大小写转换
            result = hex_str.upper() if hex_case.lower() == "upper" else hex_str.lower()
        case "int":
            result = int.from_bytes(digest, byteorder="big")
        case _:
            raise ValueError(f"不支持的输出类型: {output_type}（支持：bytes/hex/int）")

    return result, actual_length


if __name__ == "__main__":
    ct = '110010100000'[::-1]
    hamming = HammingCode()
    res = hamming.verify(ct)['corrected_code'][::-1]
    print(f'flag{{{hash_data(res, 'md5')[0]}}}')

    # flag{d14084c7ceca6359eaac6df3c234dd3b}

1.16 [BJDCTF2020]编码与调制

1.16.1 题目

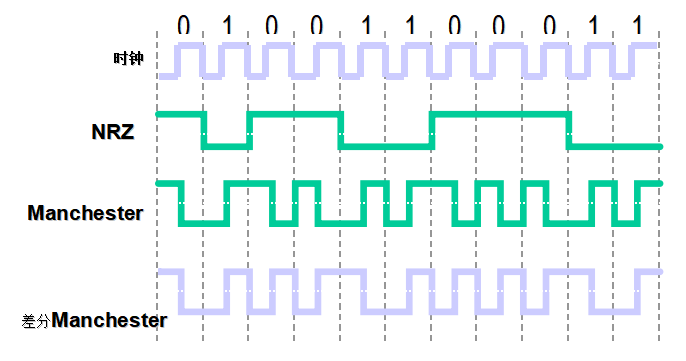
1
密文：2559659965656A9A65656996696965A6695669A9695A699569666A5A6A6569666A59695A69AA696569666AA6

1.16.2 解题思路

标准曼彻斯特编码 + 进制转换

1.16.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
from Crypto.Util.number import long_to_bytes

def convert_base(num_str: str, from_base: int, to_base: int, zfill: int = 0) -> str:
    """
    通用进制转换函数，支持填充位数
    """
    if not (2 <= from_base <= 36 and 2 <= to_base <= 36):
        raise ValueError("进制必须在 2 到 36 之间")

    digits = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"

    # 将输入字符串转换为10进制整数
    num_str = num_str.strip().upper()
    num = 0
    for char in num_str:
        val = digits.find(char)
        if val == -1 or val >= from_base:
            raise ValueError(f"非法字符 '{char}' 对于进制 {from_base}")
        num = num * from_base + val

    # 特殊情况：输入为 0
    if num == 0:
        return "0".zfill(zfill)

    # 转换为目标进制
    result = ""
    while num > 0:
        result = digits[num % to_base] + result
        num //= to_base

    return result.zfill(zfill)


class ManchesterDecoder:
    @staticmethod
    def byteinvert(str_bin):
        # 字节内位反转（8位为一组）
        ret = ''
        for i in range(len(str_bin) // 8):
            ret += str_bin[i*8:i*8+8][::-1]
        return ret

    # ---------- 解码函数 ----------

    @staticmethod
    def MCST_stand_decode(str_bin, isinvert=False):
        # 标准曼彻斯特解码（Standard Manchester Encoding）
        # 规则：0 -> 01，1 -> 10
        ret = ''
        for i in range(len(str_bin) // 2):
            x = str_bin[i*2:i*2+2]
            if x == '01':
                ret += '0'
            elif x == '10':
                ret += '1'
            else:
                return '标准曼彻斯特解码错误！'
        if isinvert:
            return ManchesterDecoder.byteinvert(ret)
        else:
            return ret

    @staticmethod
    def MCST_IEEE_decode(str_bin, isinvert=False):
        # IEEE 802.3 曼彻斯特解码（逻辑与标准相反）
        # 规则：0 -> 10，1 -> 01
        ret = ''
        for i in range(len(str_bin) // 2):
            x = str_bin[i*2:i*2+2]
            if x == '01':
                ret += '1'
            elif x == '10':
                ret += '0'
            else:
                return 'IEEE曼彻斯特解码错误！'
        if isinvert:
            return ManchesterDecoder.byteinvert(ret)
        else:
            return ret

    @staticmethod
    def MCST_diff_decode(str_bin, isinvert=False):
        # 差分曼彻斯特编码（Differential Manchester Encoding）解码
        # 解码逻辑：两段编码相同表示0，不同表示1
        ret = ''
        for i in range(0, len(str_bin) // 2 - 1):
            x1 = str_bin[i*2:i*2+2]
            x2 = str_bin[i*2+2:i*2+4]
            if x1 == x2:
                ret += '0'
            else:
                ret += '1'
        if isinvert:
            return ManchesterDecoder.byteinvert(ret)
        else:
            return ret

    # ---------- 编码函数 ----------

    @staticmethod
    def MCST_stand_encode(bit_str, isinvert=False):
        # 标准曼彻斯特编码
        # 0 -> 01，1 -> 10
        if isinvert:
            bit_str = ManchesterDecoder.byteinvert(bit_str)
        ret = ''
        for bit in bit_str:
            if bit == '0':
                ret += '01'
            elif bit == '1':
                ret += '10'
            else:
                raise ValueError('输入必须是二进制字符串')
        return ret

    @staticmethod
    def MCST_IEEE_encode(bit_str, isinvert=False):
        # IEEE 802.3 曼彻斯特编码
        # 0 -> 10，1 -> 01
        if isinvert:
            bit_str = ManchesterDecoder.byteinvert(bit_str)
        ret = ''
        for bit in bit_str:
            if bit == '0':
                ret += '10'
            elif bit == '1':
                ret += '01'
            else:
                raise ValueError('输入必须是二进制字符串')
        return ret

    @staticmethod
    def MCST_diff_encode(bit_str, isinvert=False):
        # 差分曼彻斯特编码
        # 差分曼彻斯特编码以一个初始状态开始，0表示保持前半周期电平不变，1表示反转
        # 这里用'01'和'10'代表两种状态，初始状态为'01'
        if isinvert:
            bit_str = ManchesterDecoder.byteinvert(bit_str)
        ret = ''
        prev = '0'  # 假设初始电平为0，对应编码'01'
        for bit in bit_str:
            if bit == '0':
                # 0表示信号电平保持不变，编码为与上一个一样
                if prev == '0':
                    ret += '01'
                else:
                    ret += '10'
            elif bit == '1':
                # 1表示电平反转，编码为与上一个相反
                if prev == '0':
                    ret += '10'
                    prev = '1'
                else:
                    ret += '01'
                    prev = '0'
            else:
                raise ValueError('输入必须是二进制字符串')
        return ret


if __name__ == '__main__':
    ct = "2559659965656A9A65656996696965A6695669A9695A699569666A5A6A6569666A59695A69AA696569666AA6"
    ct = convert_base(ct, 16, 2)

    result = ManchesterDecoder.MCST_stand_decode(ct, False)
    print(long_to_bytes(int(result, 2)))

    # b'BJD{DifManchestercode}'

2. 传统古典密码

2.1 看我回旋踢

2.1.1 题目

1
synt{5pq1004q-86n5-46q8-o720-oro5on0417r1}

2.1.2 解题思路

ROT18

2.1.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
class RotCipher:
    """ROT系列加密算法实现（支持ROT3/5/10/13/18/47/ROT-5/ROT-6）"""
    @staticmethod
    def _rotate_char(char: str, base: int, shift: int, range_size: int) -> str:
        """对单个字符进行指定偏移量的 ROT 加密/解密"""
        if not char.isspace():  # 跳过空白字符
            char_code = ord(char)
            if base <= char_code < base + range_size:
                # 计算旋转后的字符代码
                char_code = (char_code - base + shift) % range_size + base
            return chr(char_code)
        return char

    @staticmethod
    def rot3(text: str, decrypt: bool = False) -> str:
        """ Caesar Cipher 执行 ROT3 加密/解密，字母旋转3位 """
        shift = -3 if decrypt else 3
        result = []
        for c in text:
            if c.isupper():
                result.append(RotCipher._rotate_char(c, 65, shift, 26))
            elif c.islower():
                result.append(RotCipher._rotate_char(c, 97, shift, 26))
            else:
                result.append(c)
        return ''.join(result)
    
    @staticmethod
    def rot5(text: str, decrypt: bool = False) -> str:
        """执行ROT5加密/解密（数字旋转5位）"""
        shift = -5 if decrypt else 5
        return ''.join(RotCipher._rotate_char(c, 48, shift, 10) for c in text)
    
    @staticmethod
    def rot10(text: str, decrypt: bool = False) -> str:
        """ Avocat 执行 ROT10 加密/解密，字母旋转10位 """
        shift = -10 if decrypt else 10
        result = []
        for c in text:
            if c.isupper():
                result.append(RotCipher._rotate_char(c, 65, shift, 26))
            elif c.islower():
                result.append(RotCipher._rotate_char(c, 97, shift, 26))
            else:
                result.append(c)
        return ''.join(result)
    
    @staticmethod
    def rot13(text: str, decrypt: bool = False) -> str:
        """执行 ROT13 加密/解密（字母旋转13位）"""
        shift = -13 if decrypt else 13
        result = []
        for c in text:
            if c.isupper():
                result.append(RotCipher._rotate_char(c, 65, shift, 26))
            elif c.islower():
                result.append(RotCipher._rotate_char(c, 97, shift, 26))
            else:
                result.append(c)
        return ''.join(result)
    
    @staticmethod
    def rot18(text: str, decrypt: bool = False) -> str:
        """执行 ROT18 加密/解密（字母旋转13位 + 数字旋转5位）"""
        if not decrypt:
            return RotCipher.rot5(RotCipher.rot13(text))
        else:
            return RotCipher.rot13(RotCipher.rot5(text, decrypt=True), decrypt=True)
    
    @staticmethod
    def rot47(text: str, decrypt: bool = False) -> str:
        """执行 ROT47 加密/解密（ASCII 33-126 旋转47位）"""
        shift = -47 if decrypt else 47
        return ''.join(RotCipher._rotate_char(c, 33, shift, 94) for c in text)
    
    @staticmethod
    def rot_neg5(text: str, decrypt: bool = False) -> str:
        """ Cassis 执行 ROT-5 加密/解密，数字反向旋转5位"""
        shift = 5 if decrypt else -5  # 反向旋转
        return ''.join(RotCipher._rotate_char(c, 48, shift, 10) for c in text)
    
    @staticmethod
    def rot_neg6(text: str, decrypt: bool = False) -> str:
        """Cassette 执行 ROT-6 加密/解密（字母反向旋转6位，保留大小写）"""
        shift = 6 if decrypt else -6  # 反向旋转
        result = []
        for c in text:
            if c.isupper():
                result.append(RotCipher._rotate_char(c, 65, shift, 26))
            elif c.islower():
                result.append(RotCipher._rotate_char(c, 97, shift, 26))
            else:
                result.append(c)
        return ''.join(result)

    @staticmethod
    def shift_cipher(text: str, offset: int = None, alphabet: str = None) -> dict | str:
        """
        通用移位密码实现
        """
        if alphabet is None:
            # 默认使用标准字母表（大小写字母）
            alphabet_upper = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
            alphabet_lower = "abcdefghijklmnopqrstuvwxyz"
            
            if offset is not None:
                result = []
                for c in text:
                    if c.isupper():
                        idx = (alphabet_upper.index(c) + offset) % 26
                        result.append(alphabet_upper[idx])
                    elif c.islower():
                        idx = (alphabet_lower.index(c) + offset) % 26
                        result.append(alphabet_lower[idx])
                    else:
                        result.append(c)
                return ''.join(result)
            else:
                results = {}
                for o in range(1, 27):  # 字母表长度为26
                    results[o] = RotCipher.shift_cipher(text, o, alphabet)
                return results
        else:
            # 使用自定义字符表
            if offset is not None:
                result = []
                for c in text:
                    if c in alphabet:
                        idx = (alphabet.index(c) + offset) % len(alphabet)
                        result.append(alphabet[idx])
                    else:
                        result.append(c)  # 不在字符表中的字符保持不变
                return ''.join(result)
            else:
                results = {}
                for o in range(1, len(alphabet)):
                    results[o] = RotCipher.shift_cipher(text, o, alphabet)
                return results


if __name__ == '__main__':
    res = RotCipher.rot18("synt{5pq1004q-86n5-46q8-o720-oro5on0417r1}")
    print(res)

    # flag{0cd6559d-31a0-91d3-b275-beb0ba5962e6}

2.2 摩丝

2.2.1 题目

1
.. .-.. --- ...- . -.-- --- ..-

2.2.2 解题思路

Morse 密码

2.2.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class MorseCode:
    """摩斯密码加解密类"""

    def __init__(self):
        # 字符到摩斯码映射表
        self.char_to_morse = {
            'A': '.-', 'B': '-...', 'C': '-.-.', 'D': '-..', 'E': '.',
            'F': '..-.', 'G': '--.', 'H': '....', 'I': '..', 'J': '.---',
            'K': '-.-', 'L': '.-..', 'M': '--', 'N': '-.', 'O': '---',
            'P': '.--.', 'Q': '--.-', 'R': '.-.', 'S': '...', 'T': '-',
            'U': '..-', 'V': '...-', 'W': '.--', 'X': '-..-', 'Y': '-.--', 'Z': '--..',
            '0': '-----', '1': '.----', '2': '..---', '3': '...--', '4': '....-',
            '5': '.....', '6': '-....', '7': '--...', '8': '---..', '9': '----.',
            '.': '.-.-.-', ',': '--..--', '?': '..--..', "'": '.----.', '!': '-.-.--',
            '/': '-..-.', '(': '-.--.', ')': '-.--.-', '&': '.-...', ':': '---...',
            ';': '-.-.-.', '=': '-...-', '+': '.-.-.', '-': '-....-', '_': '..--.-',
            '"': '.-..-.', '$': '...-..-', '@': '.--.-.', ' ': '/'
        }
        # 摩斯码到字符的反向映射
        self.morse_to_char = {v: k for k, v in self.char_to_morse.items()}

    def encrypt(self, text: str) -> str:
        """将普通文本加密为摩斯密码"""
        return ' '.join(
            self.char_to_morse.get(char.upper(), char) for char in text
        )

    def decrypt(self, morse_code: str) -> str:
        """将摩斯密码解密为普通文本"""
        # 用空格分割每个摩斯字符
        morse_list = morse_code.strip().split(' ')
        decoded_chars = []

        for code in morse_list:
            if code == '/':  # 单词分隔符
                decoded_chars.append(' ')
            else:
                decoded_chars.append(self.morse_to_char.get(code, code))  # 转换或保留原样

        return ''.join(decoded_chars)


if __name__ == "__main__":
    ciphertext = ".. .-.. --- ...- . -.-- --- ..-"
    decrypted = MorseCode().decrypt(ciphertext)
    print(f"解密: {ciphertext} → {decrypted}")
    print(f"flag{{{decrypted}}}")
    
    # flag{ILOVEYOU}

2.3 变异凯撒

2.3.1 题目

1
2
加密密文：afZ_r9VYfScOeO_UL^RWUc
格式：flag{ }

2.3.2 解题思路

密文前四位 afZ_ 对应明文 flag，可推测该加密方式为变种凯撒加密：每个字符按递增偏移量依次加密，首位偏移 5 位，之后逐位加 1。

2.3.3 解题脚本

1
2
3
4
5
6
if __name__ == '__main__':
    ct = "afZ_r9VYfScOeO_UL^RWUc"
    pt = ''.join(chr(ord(c) + 5 + i) for i, c in enumerate(ct))
    print(pt)

    # flag{Caesar_variation}

2.4 篱笆墙的影子

2.4.1 题目

1
2
3
星星还是那颗星星哟 月亮还是那个月亮 山也还是那座山哟 梁也还是那道梁 碾子是碾子 缸是缸哟 爹是爹来娘是娘 麻油灯呵还吱吱响 点的还是那么丁点亮 哦哦 注意：得到的 flag 请包上 flag{} 提交

felhaagv{ewtehtehfilnakgw}

2.4.2 解题思路

栅栏密码（key = 13）

2.4.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
import math


class Railfence:
    @staticmethod
    def encrypt(message, key=None):
        """
        加密函数：实现 Rail Fence Cipher 的分段加密。
        """
        if key is not None:
            ciphertext = ''
            for i in range(key):
                ciphertext += message[i::key]
            return ciphertext
        else:
            # 遍历 key 从 2 到 12
            results = {}
            for k in range(2, 13):
                ciphertext = ''
                for i in range(k):
                    ciphertext += message[i::k]
                results[k] = ciphertext
            return results

    @staticmethod
    def decrypt(ciphertext, key=None):
        """
        解密函数：根据密文和密钥 key 还原原文。
        """
        if key is not None:
            plaintext = ''
            row_length = math.ceil(len(ciphertext) / key)
            for i in range(row_length):
                plaintext += ciphertext[i::row_length]
            return plaintext
        else:
            # 遍历 key 从 2 到 16
            results = {}
            for k in range(2, 17):
                row_length = math.ceil(len(ciphertext) / k)
                plaintext = ''
                for i in range(row_length):
                    plaintext += ciphertext[i::row_length]
                results[k] = plaintext
            return results


if __name__ == '__main__':
    ciphertext = r"felhaagv{ewtehtehfilnakgw}"
    print(Railfence.decrypt(ciphertext))

    # flag{wethinkwehavetheflag}

2.5 大帝的密码武器

2.5.1 题目

1
2
3
4
5
6
7
# 密文
ComeChina

# 题目
公元前一百年，在罗马出生了一位对世界影响巨大的人物，他生前是罗马三巨头之一。他率先使用了一种简单的加密函，因此这种加密方法以他的名字命名。
以下密文被解开后可以获得一个有意义的单词：FRPHEVGL
你可以用这个相同的加密向量加密附件中的密文，作为答案进行提交。

2.5.2 解题思路

使用凯撒密码解密 FRPHEVGL，得到有意义单词 SECURITY。得到偏移量13（ROT13），使用该密钥对 ComeChina 进行加密。

2.5.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
class RotCipher:
    """ROT系列加密算法实现（支持ROT3/5/10/13/18/47/ROT-5/ROT-6）"""
    @staticmethod
    def _rotate_char(char: str, base: int, shift: int, range_size: int) -> str:
        """对单个字符进行指定偏移量的 ROT 加密/解密"""
        if not char.isspace():  # 跳过空白字符
            char_code = ord(char)
            if base <= char_code < base + range_size:
                # 计算旋转后的字符代码
                char_code = (char_code - base + shift) % range_size + base
            return chr(char_code)
        return char

    @staticmethod
    def rot3(text: str, decrypt: bool = False) -> str:
        """ Caesar Cipher 执行 ROT3 加密/解密，字母旋转3位 """
        shift = -3 if decrypt else 3
        result = []
        for c in text:
            if c.isupper():
                result.append(RotCipher._rotate_char(c, 65, shift, 26))
            elif c.islower():
                result.append(RotCipher._rotate_char(c, 97, shift, 26))
            else:
                result.append(c)
        return ''.join(result)
    
    @staticmethod
    def rot5(text: str, decrypt: bool = False) -> str:
        """执行ROT5加密/解密（数字旋转5位）"""
        shift = -5 if decrypt else 5
        return ''.join(RotCipher._rotate_char(c, 48, shift, 10) for c in text)
    
    @staticmethod
    def rot10(text: str, decrypt: bool = False) -> str:
        """ Avocat 执行 ROT10 加密/解密，字母旋转10位 """
        shift = -10 if decrypt else 10
        result = []
        for c in text:
            if c.isupper():
                result.append(RotCipher._rotate_char(c, 65, shift, 26))
            elif c.islower():
                result.append(RotCipher._rotate_char(c, 97, shift, 26))
            else:
                result.append(c)
        return ''.join(result)
    
    @staticmethod
    def rot13(text: str, decrypt: bool = False) -> str:
        """执行 ROT13 加密/解密（字母旋转13位）"""
        shift = -13 if decrypt else 13
        result = []
        for c in text:
            if c.isupper():
                result.append(RotCipher._rotate_char(c, 65, shift, 26))
            elif c.islower():
                result.append(RotCipher._rotate_char(c, 97, shift, 26))
            else:
                result.append(c)
        return ''.join(result)
    
    @staticmethod
    def rot18(text: str, decrypt: bool = False) -> str:
        """执行 ROT18 加密/解密（字母旋转13位 + 数字旋转5位）"""
        if not decrypt:
            return RotCipher.rot5(RotCipher.rot13(text))
        else:
            return RotCipher.rot13(RotCipher.rot5(text, decrypt=True), decrypt=True)
    
    @staticmethod
    def rot47(text: str, decrypt: bool = False) -> str:
        """执行 ROT47 加密/解密（ASCII 33-126 旋转47位）"""
        shift = -47 if decrypt else 47
        return ''.join(RotCipher._rotate_char(c, 33, shift, 94) for c in text)
    
    @staticmethod
    def rot_neg5(text: str, decrypt: bool = False) -> str:
        """ Cassis 执行 ROT-5 加密/解密，数字反向旋转5位"""
        shift = 5 if decrypt else -5  # 反向旋转
        return ''.join(RotCipher._rotate_char(c, 48, shift, 10) for c in text)
    
    @staticmethod
    def rot_neg6(text: str, decrypt: bool = False) -> str:
        """Cassette 执行 ROT-6 加密/解密（字母反向旋转6位，保留大小写）"""
        shift = 6 if decrypt else -6  # 反向旋转
        result = []
        for c in text:
            if c.isupper():
                result.append(RotCipher._rotate_char(c, 65, shift, 26))
            elif c.islower():
                result.append(RotCipher._rotate_char(c, 97, shift, 26))
            else:
                result.append(c)
        return ''.join(result)

    @staticmethod
    def shift_cipher(text: str, offset: int = None, alphabet: str = None) -> dict | str:
        """
        通用移位密码实现
        """
        if alphabet is None:
            # 默认使用标准字母表（大小写字母）
            alphabet_upper = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
            alphabet_lower = "abcdefghijklmnopqrstuvwxyz"
            
            if offset is not None:
                result = []
                for c in text:
                    if c.isupper():
                        idx = (alphabet_upper.index(c) + offset) % 26
                        result.append(alphabet_upper[idx])
                    elif c.islower():
                        idx = (alphabet_lower.index(c) + offset) % 26
                        result.append(alphabet_lower[idx])
                    else:
                        result.append(c)
                return ''.join(result)
            else:
                results = {}
                for o in range(1, 27):  # 字母表长度为26
                    results[o] = RotCipher.shift_cipher(text, o, alphabet)
                return results
        else:
            # 使用自定义字符表
            if offset is not None:
                result = []
                for c in text:
                    if c in alphabet:
                        idx = (alphabet.index(c) + offset) % len(alphabet)
                        result.append(alphabet[idx])
                    else:
                        result.append(c)  # 不在字符表中的字符保持不变
                return ''.join(result)
            else:
                results = {}
                for o in range(1, len(alphabet)):
                    results[o] = RotCipher.shift_cipher(text, o, alphabet)
                return results


if __name__ == '__main__':
    print(RotCipher.shift_cipher("FRPHEVGL"))
    pt = RotCipher.rot13("ComeChina")
    print(f'flag{{{pt}}}')

    # flag{PbzrPuvan}

2.6 凯撒？替换？呵呵!

2.6.1 题目

1
MTHJ{CUBCGXGUGXWREXIPOYAOEYFIGXWRXCHTKHFCOHCFDUCGTXZOHIXOEOWMEHZO}

2.6.2 解题思路

随机替换密码：一种将明文字母唯一且混乱地替换为不同字母的加密方法，密码字母表完全打乱，短密文需知晓字母对应规则才能解密，长密文则通常借助词频分析破译。使用 http://quipqiup.com/ 词频分析。

2.6.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
import requests
import urllib3

# 忽略 SSL 证书警告
urllib3.disable_warnings(urllib3.exceptions.InsecureRequestWarning)

def decrypt_with_quipqiup(ciphertext: str, clues: str= "") -> dict:
    """
    使用 quipqiup.com 对替换加密密文进行自动解密。
    """
    headers = {
        "Accept": "*/*",
        "Accept-Language": "zh-CN,zh;q=0.9,en;q=0.8,en-GB;q=0.7,en-US;q=0.6",
        "Content-type": "application/x-www-form-urlencoded",
        "Origin": "http://quipqiup.com",
        "Referer": "http://quipqiup.com/",
        "User-Agent": "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/136.0.0.0 Safari/537.36 Edg/136.0.0.0",
    }

    payload = {
        "ciphertext": ciphertext,
        "clues": clues,
        "mode": "auto",
        "was_auto": True,
        "was_clue": False,
    }

    # 请求提交密文以开始解密
    try:
        response = requests.post("http://quipqiup.com/solve", headers=headers, json=payload, verify=False)
        response.raise_for_status()
        id_payload = {"id": response.json().get("id")}
    except Exception as e:
        print("提交解密请求失败:", e)
        return {}

    # 请求获取解密结果
    try:
        response = requests.post("http://quipqiup.com/status", headers=headers, json=id_payload, verify=False)
        response.raise_for_status()
        solutions = response.json().get("solutions", [])
    except Exception as e:
        print("获取解密结果失败:", e)
        return {}

    # 组织解密结果
    result = {}
    for s in solutions:
        result[s["key"]] = s["plaintext"]
    return result


if __name__ == '__main__':
    cipher = "MTHJ{CUBCGXGUGXWREXIPOYAOEYFIGXWRXCHTKHFCOHCFDUCGTXZOHIXOEOWMEHZO}"
    result = decrypt_with_quipqiup(cipher, clues="MTHJ = flag")
    for key, text in result.items():
        if 'flag' in text:
            print(f"Key: {key}\nPlaintext: {text}\n")

            # flag{substitutioncipherdecryptionisalwayseasyjustlikeapieceofcake}

2.7 萌萌哒的八戒

2.7.1 题目

2.7.2 解题思路

猪圈密码

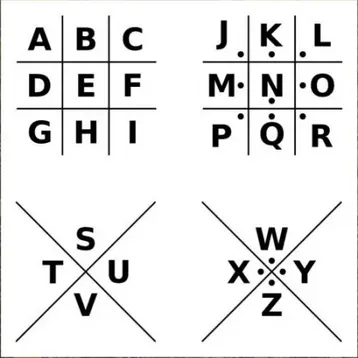
2.7.3 解题脚本

flag{whenthepigwanttoeat}


2.8 传统知识+古典密码

2.8.1 题目

1
2
3
4
5
小明某一天收到一封密信，信中写了几个不同的年份
          辛卯，癸巳，丙戌，辛未，庚辰，癸酉，己卯，癸巳。
          信的背面还写有“+甲子”，请解出这段密文。

key值：CTF{XXX}

2.8.2 解题思路

天干地支加密 + 栅栏密码（key=2）+ 凯撒密码（key=21）

2.8.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
import math

class tiangan_dizhi:
    ganzhi_dict = {
        1: "甲子", 2: "乙丑", 3: "丙寅", 4: "丁卯", 5: "戊辰",
        6: "己巳", 7: "庚午", 8: "辛未", 9: "壬申", 10: "癸酉",
        11: "甲戌", 12: "乙亥", 13: "丙子", 14: "丁丑", 15: "戊寅",
        16: "己卯", 17: "庚辰", 18: "辛巳", 19: "壬午", 20: "癸未",
        21: "甲申", 22: "乙酉", 23: "丙戌", 24: "丁亥", 25: "戊子",
        26: "己丑", 27: "庚寅", 28: "辛卯", 29: "壬辰", 30: "癸巳",
        31: "甲午", 32: "乙未", 33: "丙申", 34: "丁酉", 35: "戊戌",
        36: "己亥", 37: "庚子", 38: "辛丑", 39: "壬寅", 40: "癸卯",
        41: "甲辰", 42: "乙巳", 43: "丙午", 44: "丁未", 45: "戊申",
        46: "己酉", 47: "庚戌", 48: "辛亥", 49: "壬子", 50: "癸丑",
        51: "甲寅", 52: "乙卯", 53: "丙辰", 54: "丁巳", 55: "戊午",
        56: "己未", 57: "庚申", 58: "辛酉", 59: "壬戌", 60: "癸亥"
    }
    reverse_dict = {v: k for k, v in ganzhi_dict.items()}

    @classmethod
    def decrypt(cls, ganzhi_list):
        """
        将干支列表转换为对应的数字列表
        """
        result = []
        for item in ganzhi_list:
            if item in cls.reverse_dict:
                result.append(cls.reverse_dict[item])
            else:
                raise ValueError(f"无效的干支字符串: {item}")
        return result

    @classmethod
    def encrypt(cls, number_list):
        """
        将数字列表转换为对应的干支列表
        """
        result = []
        for num in number_list:
            if 1 <= num <= 60:
                result.append(cls.ganzhi_dict[num])
            else:
                raise ValueError(f"数字超出范围 (1-60): {num}")
        return result

class Railfence:
    @staticmethod
    def encrypt(message, key=None):
        """
        加密函数：实现 Rail Fence Cipher 的分段加密。
        """
        if key is not None:
            ciphertext = ''
            for i in range(key):
                ciphertext += message[i::key]
            return ciphertext
        else:
            # 遍历 key 从 2 到 12
            results = {}
            for k in range(2, 13):
                ciphertext = ''
                for i in range(k):
                    ciphertext += message[i::k]
                results[k] = ciphertext
            return results

    @staticmethod
    def decrypt(ciphertext, key=None):
        """
        解密函数：根据密文和密钥 key 还原原文。
        """
        if key is not None:
            plaintext = ''
            row_length = math.ceil(len(ciphertext) / key)
            for i in range(row_length):
                plaintext += ciphertext[i::row_length]
            return plaintext
        else:
            # 遍历 key 从 2 到 12
            results = {}
            for k in range(2, 13):
                row_length = math.ceil(len(ciphertext) / k)
                plaintext = ''
                for i in range(row_length):
                    plaintext += ciphertext[i::row_length]
                results[k] = plaintext
            return results

class RotCipher:
    """ROT系列加密算法实现（支持ROT3/5/10/13/18/47/ROT-5/ROT-6）"""
    @staticmethod
    def _rotate_char(char: str, base: int, shift: int, range_size: int) -> str:
        """对单个字符进行指定偏移量的 ROT 加密/解密"""
        if not char.isspace():  # 跳过空白字符
            char_code = ord(char)
            if base <= char_code < base + range_size:
                # 计算旋转后的字符代码
                char_code = (char_code - base + shift) % range_size + base
            return chr(char_code)
        return char

    @staticmethod
    def shift_cipher(text: str, offset: int = None, alphabet: str = None) -> dict | str:
        """
        通用移位密码实现
        """
        if alphabet is None:
            # 默认使用标准字母表（大小写字母）
            alphabet_upper = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
            alphabet_lower = "abcdefghijklmnopqrstuvwxyz"
            
            if offset is not None:
                result = []
                for c in text:
                    if c.isupper():
                        idx = (alphabet_upper.index(c) + offset) % 26
                        result.append(alphabet_upper[idx])
                    elif c.islower():
                        idx = (alphabet_lower.index(c) + offset) % 26
                        result.append(alphabet_lower[idx])
                    else:
                        result.append(c)
                return ''.join(result)
            else:
                results = {}
                for o in range(1, 27):  # 字母表长度为26
                    results[o] = RotCipher.shift_cipher(text, o, alphabet)
                return results
        else:
            # 使用自定义字符表
            if offset is not None:
                result = []
                for c in text:
                    if c in alphabet:
                        idx = (alphabet.index(c) + offset) % len(alphabet)
                        result.append(alphabet[idx])
                    else:
                        result.append(c)  # 不在字符表中的字符保持不变
                return ''.join(result)
            else:
                results = {}
                for o in range(1, len(alphabet)):
                    results[o] = RotCipher.shift_cipher(text, o, alphabet)
                return results


if __name__ == "__main__":
    encrypted = tiangan_dizhi.decrypt(["辛卯", "癸巳", "丙戌", "辛未", "庚辰", "癸酉", "己卯", "癸巳"])
    msg1 = "".join([chr(i + 60) for i in encrypted])
    msg2 = Railfence.decrypt(msg1, 2)
    msg3 = RotCipher.shift_cipher(msg2, 21)
    print(f'CTF{{{msg3}}}')

    # CTF{SHUANGYU}

2.9 世上无难事

2.9.1 题目

1
2
3
以下是某国现任总统外发的一段指令，经过一种奇异的加密方式，毫无规律，看来只能分析了。请将这段语句还原成通顺语句，并从中找到key作为答案提交，答案是32位，包含小写字母。

VIZZB IFIUOJBWO NVXAP OBC XZZ UKHVN IFIUOJBWO HB XVIXW XAW VXFI X QIXN VBD KQ IFIUOJBWO WBKAH NBWXO VBD XJBCN NKG QLKEIU DI XUI VIUI DKNV QNCWIANQ XN DXPIMKIZW VKHV QEVBBZ KA XUZKAHNBA FKUHKAKX XAW DI VXFI HBN QNCWIANQ NCAKAH KA MUBG XZZ XEUBQQ XGIUKEX MUBG PKAWIUHXUNIA NVUBCHV 12NV HUXWI XAW DI XUI SCQN QB HZXW NVXN XZZ EBCZW SBKA CQ NBWXO XAW DI DXAN NB NVXAP DXPIMKIZW MBU JIKAH QCEV XA BCNQNXAWKAH VBQN HKFI OBCUQIZFIQ X JKH UBCAW BM XLLZXCQI XAW NVI PIO KQ 640I11012805M211J0XJ24MM02X1IW09

2.9.2 解题思路

随机替换密码：使用 http://quipqiup.com/ 词频分析。

2.9.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
import requests
import urllib3

# 忽略 SSL 证书警告
urllib3.disable_warnings(urllib3.exceptions.InsecureRequestWarning)

def decrypt_with_quipqiup(ciphertext: str, clues: str= "") -> dict:
    """
    使用 quipqiup.com 对替换加密密文进行自动解密。
    """
    headers = {
        "Accept": "*/*",
        "Accept-Language": "zh-CN,zh;q=0.9,en;q=0.8,en-GB;q=0.7,en-US;q=0.6",
        "Content-type": "application/x-www-form-urlencoded",
        "Origin": "http://quipqiup.com",
        "Referer": "http://quipqiup.com/",
        "User-Agent": "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/136.0.0.0 Safari/537.36 Edg/136.0.0.0",
    }

    payload = {
        "ciphertext": ciphertext,
        "clues": clues,
        "mode": "auto",
        "was_auto": True,
        "was_clue": False,
    }

    # 请求提交密文以开始解密
    try:
        response = requests.post("http://quipqiup.com/solve", headers=headers, json=payload, verify=False)
        response.raise_for_status()
        id_payload = {"id": response.json().get("id")}
    except Exception as e:
        print("提交解密请求失败:", e)
        return {}

    # 请求获取解密结果
    try:
        response = requests.post("http://quipqiup.com/status", headers=headers, json=id_payload, verify=False)
        response.raise_for_status()
        solutions = response.json().get("solutions", [])
    except Exception as e:
        print("获取解密结果失败:", e)
        return {}

    # 组织解密结果
    result = {}
    for s in solutions:
        result[s["key"]] = s["plaintext"]
    return result



if __name__ == '__main__':
    cipher = "VIZZB IFIUOJBWO NVXAP OBC XZZ UKHVN IFIUOJBWO HB XVIXW XAW VXFI X QIXN VBD KQ IFIUOJBWO WBKAH NBWXO VBD XJBCN NKG QLKEIU DI XUI VIUI DKNV QNCWIANQ XN DXPIMKIZW VKHV QEVBBZ KA XUZKAHNBA FKUHKAKX XAW DI VXFI HBN QNCWIANQ NCAKAH KA MUBG XZZ XEUBQQ XGIUKEX MUBG PKAWIUHXUNIA NVUBCHV 12NV HUXWI XAW DI XUI SCQN QB HZXW NVXN XZZ EBCZW SBKA CQ NBWXO XAW DI DXAN NB NVXAP DXPIMKIZW MBU JIKAH QCEV XA BCNQNXAWKAH VBQN HKFI OBCUQIZFIQ X JKH UBCAW BM XLLZXCQI XAW NVI PIO KQ 640I11012805M211J0XJ24MM02X1IW09"
    result = decrypt_with_quipqiup(cipher)
    for key, text in result.items():
        print(f"Key: {key}\nPlaintext: {text}\n")
        break
    
        # flag{640E11012805F211B0AB24FF02A1ED09}

2.10 old-fashion

2.10.1 题目

1
Os drnuzearyuwn, y jtkjzoztzoes douwlr oj y ilzwex eq lsdexosa kn pwodw tsozj eq ufyoszlbz yrl rlufydlx pozw douwlrzlbz, ydderxosa ze y rlatfyr jnjzli; mjy gfbmw vla xy wbfnsy symmyew (mjy vrwm qrvvrf), hlbew rd symmyew, mebhsymw rd symmyew, vbomgeyw rd mjy lxrzy, lfk wr dremj. Mjy eyqybzye kyqbhjyew mjy myom xa hyedrevbfn lf bfzyewy wgxwmbmgmbrf. Wr mjy dsln bw f1_2jyf-k3_jg1-vb-vl_l

2.10.2 解题思路

随机替换密码：使用 http://quipqiup.com/ 词频分析。

2.10.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
import requests
import urllib3

# 忽略 SSL 证书警告
urllib3.disable_warnings(urllib3.exceptions.InsecureRequestWarning)

def decrypt_with_quipqiup(ciphertext: str, clues: str= "") -> dict:
    """
    使用 quipqiup.com 对替换加密密文进行自动解密。
    """
    headers = {
        "Accept": "*/*",
        "Accept-Language": "zh-CN,zh;q=0.9,en;q=0.8,en-GB;q=0.7,en-US;q=0.6",
        "Content-type": "application/x-www-form-urlencoded",
        "Origin": "http://quipqiup.com",
        "Referer": "http://quipqiup.com/",
        "User-Agent": "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/136.0.0.0 Safari/537.36 Edg/136.0.0.0",
    }

    payload = {
        "ciphertext": ciphertext,
        "clues": "",
        "mode": "auto",
        "was_auto": True,
        "was_clue": False,
    }

    # 请求提交密文以开始解密
    try:
        response = requests.post("http://quipqiup.com/solve", headers=headers, json=payload, verify=False)
        response.raise_for_status()
        id_payload = {"id": response.json().get("id")}
    except Exception as e:
        print("提交解密请求失败:", e)
        return {}

    # 请求获取解密结果
    try:
        response = requests.post("http://quipqiup.com/status", headers=headers, json=id_payload, verify=False)
        response.raise_for_status()
        solutions = response.json().get("solutions", [])
    except Exception as e:
        print("获取解密结果失败:", e)
        return {}

    # 组织解密结果
    result = {}
    for s in solutions:
        result[s["key"]] = s["plaintext"]
    return result



if __name__ == '__main__':
    cipher = "Os drnuzearyuwn, y jtkjzoztzoes douwlr oj y ilzwex eq lsdexosa kn pwodw tsozj eq ufyoszlbz yrl rlufydlx pozw douwlrzlbz, ydderxosa ze y rlatfyr jnjzli; mjy gfbmw vla xy wbfnsy symmyew (mjy vrwm qrvvrf), hlbew rd symmyew, mebhsymw rd symmyew, vbomgeyw rd mjy lxrzy, lfk wr dremj. Mjy eyqybzye kyqbhjyew mjy myom xa hyedrevbfn lf bfzyewy wgxwmbmgmbrf. Wr mjy dsln bw f1_2jyf-k3_jg1-vb-vl_l"

    result = decrypt_with_quipqiup(cipher)
    for key, text in result.items():
        if 'flag' in text:
            print(f"Key: {key}\nPlaintext: {text}\n")

            # flag{n1_2hen-d3_hu1-mi-ma_a}

2.11 [AFCTF2018]Morse

2.11.1 题目

1
-..../.----/-..../-..../-..../...--/--.../....-/-..../-..../--.../-.../...--/.----/--.../...--/..---/--.../--.../....-/...../..-./--.../...--/...--/-----/...../..-./...--/...--/...--/....-/...--/...../--.../----./--.../-..

2.11.2 解题思路

Morse 密码

2.11.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class MorseCode:
    """摩斯密码加解密类"""
    
    def __init__(self):
        # 字符到摩斯码映射表
        self.char_to_morse = {
            'A': '.-', 'B': '-...', 'C': '-.-.', 'D': '-..', 'E': '.',
            'F': '..-.', 'G': '--.', 'H': '....', 'I': '..', 'J': '.---',
            'K': '-.-', 'L': '.-..', 'M': '--', 'N': '-.', 'O': '---',
            'P': '.--.', 'Q': '--.-', 'R': '.-.', 'S': '...', 'T': '-',
            'U': '..-', 'V': '...-', 'W': '.--', 'X': '-..-', 'Y': '-.--', 'Z': '--..',
            '0': '-----', '1': '.----', '2': '..---', '3': '...--', '4': '....-',
            '5': '.....', '6': '-....', '7': '--...', '8': '---..', '9': '----.',
            '.': '.-.-.-', ',': '--..--', '?': '..--..', "'": '.----.', '!': '-.-.--',
            '/': '-..-.', '(': '-.--.', ')': '-.--.-', '&': '.-...', ':': '---...',
            ';': '-.-.-.', '=': '-...-', '+': '.-.-.', '-': '-....-', '_': '..--.-',
            '"': '.-..-.', '$': '...-..-', '@': '.--.-.', ' ': '/'
        }
        # 摩斯码到字符的反向映射
        self.morse_to_char = {v: k for k, v in self.char_to_morse.items()}

    def encrypt(self, text: str, interval: str = ' ') -> str:
        """将普通文本加密为摩斯密码"""
        return interval.join(
            self.char_to_morse.get(char.upper(), char) for char in text
        )

    def decrypt(self, morse_code: str, interval: str = ' ') -> str:
        """将摩斯密码解密为普通文本"""
        # 用空格分割每个摩斯字符
        morse_list = morse_code.strip().split(interval)
        decoded_chars = []

        for code in morse_list:
            if code == '/':  # 单词分隔符
                decoded_chars.append(' ')
            else:
                decoded_chars.append(self.morse_to_char.get(code, code))  # 转换或保留原样

        return ''.join(decoded_chars)


if __name__ == "__main__":
    ciphertext = "-..../.----/-..../-..../-..../...--/--.../....-/-..../-..../--.../-.../...--/.----/--.../...--/..---/--.../--.../....-/...../..-./--.../...--/...--/-----/...../..-./...--/...--/...--/....-/...--/...../--.../----./--.../-.."
    decrypted = MorseCode().decrypt(ciphertext, '/')
    print(f"解密: {ciphertext} → {decrypted}")
    print(bytes.fromhex(decrypted))

    # b"afctf{1s't_s0_345y}"

2.12 [GXYCTF2019]CheckIn

2.12.1 题目

1
dikqTCpfRjA8fUBIMD5GNDkwMjNARkUwI0BFTg==

2.12.2 解题思路

Base64 编码 + ROT47

2.12.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
from base64 import b64decode


class RotCipher:
    """ROT系列加密算法实现（支持ROT3/5/10/13/18/47/ROT-5/ROT-6）"""
    @staticmethod
    def _rotate_char(char: str, base: int, shift: int, range_size: int) -> str:
        """对单个字符进行指定偏移量的 ROT 加密/解密"""
        if not char.isspace():  # 跳过空白字符
            char_code = ord(char)
            if base <= char_code < base + range_size:
                # 计算旋转后的字符代码
                char_code = (char_code - base + shift) % range_size + base
            return chr(char_code)
        return char
    
    @staticmethod
    def rot47(text: str, decrypt: bool = False) -> str:
        """执行 ROT47 加密/解密（ASCII 33-126 旋转47位）"""
        shift = -47 if decrypt else 47
        return ''.join(RotCipher._rotate_char(c, 33, shift, 94) for c in text)


if __name__ == "__main__":
    ct = b"dikqTCpfRjA8fUBIMD5GNDkwMjNARkUwI0BFTg=="
    msg = b64decode(ct).decode("utf8")
    print(RotCipher.rot47(msg))

    # GXY{Y0u_kNow_much_about_Rot}

2.13 Cipher

2.13.1 题目

1
还能提示什么呢？公平的玩吧（密钥自己找） Dncnoqqfliqrpgeklwmppu

2.13.2 解题思路

Playfair 密码（key = playfair）

2.13.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
from typing import Optional, Tuple


class Playfair:
    def __init__(self, key: Optional[str] = None):
        self._init_matrix(key)

    def _init_matrix(self, key: str):
        key = (key or "").upper().replace("J", "I")
        letters = "ABCDEFGHIKLMNOPQRSTUVWXYZ"       # 去掉 J

        # 去重并保留顺序：先 key 再剩余字母
        sequence = []
        for ch in key + letters:
            if ch.isalpha() and ch not in sequence:
                sequence.append(ch)
        
        # 构造 5x5 矩阵
        self.matrix = [sequence[i:i+5] for i in range(0, 25, 5)]

    def _find(self, ch: str) -> Tuple[int, int]:
        """
        查找字符在矩阵中的行列索引
        """
        for r, row in enumerate(self.matrix):
            if ch in row:
                return r, row.index(ch)
        raise ValueError(f"字符 {ch} 不在矩阵中")

    def _preprocess(self, text: str) -> list:
        """
        预处理明文：去空格、大写、替换 J->I，按规则分组
        """
        src = text.upper().replace(" ", "").replace("J", "I")
        pairs = []
        i = 0
        while i < len(src):
            a = src[i]
            b = src[i+1] if i+1 < len(src) else 'X'
            # 同字符或末尾补 X
            if a == b:
                pairs.append((a, 'X'))
                i += 1
            else:
                pairs.append((a, b))
                i += 2
        # 若最后剩单字符，则补 X
        if pairs and len(pairs[-1]) == 1:
            pairs[-1] = (pairs[-1][0], 'X')
        return pairs

    def _transform(self, a: str, b: str, mode: int = 1) -> str:
        """
        核心变换：mode=1 加密右下移，mode=-1 解密左上移
        """
        r1, c1 = self._find(a)
        r2, c2 = self._find(b)
        # 同行：左右移动
        if r1 == r2:
            return (self.matrix[r1][(c1 + mode) % 5] +
                    self.matrix[r2][(c2 + mode) % 5])
        # 同列：上下移动
        if c1 == c2:
            return (self.matrix[(r1 + mode) % 5][c1] +
                    self.matrix[(r2 + mode) % 5][c2])
        # 矩形对角交换列索引
        return (self.matrix[r1][c2] + self.matrix[r2][c1])

    def encrypt(self, plaintext: str) -> str:
        """
        加密明文，并返回密文字符串
        """
        pairs = self._preprocess(plaintext)
        return ''.join(self._transform(a, b, mode=1) for a, b in pairs)

    def decrypt(self, ciphertext: str) -> str:
        """
        解密密文，并返回去填充后的明文
        """
        # 分组：每两个字符一对
        ciphertext = ciphertext.upper()
        pairs = [(ciphertext[i], ciphertext[i+1]) for i in range(0, len(ciphertext), 2)]
        raw = ''.join(self._transform(a, b, mode=-1) for a, b in pairs)
        # 去掉填充 X
        return raw.replace('X', '')


if __name__ == '__main__':
    pf = Playfair('playfair')
    pt = pf.decrypt('Dncnoqqfliqrpgeklwmppu').lower()
    print(f'flag{{{pt}}}')

    # flag{itisnotaproblemhavefun}

2.14 robomunication

2.14.1 题目

摩斯密码音频：.... . .-.. .-.. --- .-- .... .- - .. ... - .... . -.- . -.-- .. - .. ... -... --- --- .--. -... . . .--.

2.14.2 解题思路

Morse 密码

2.14.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class MorseCode:
    """摩斯密码加解密类"""

    def __init__(self):
        # 字符到摩斯码映射表
        self.char_to_morse = {
            'A': '.-', 'B': '-...', 'C': '-.-.', 'D': '-..', 'E': '.',
            'F': '..-.', 'G': '--.', 'H': '....', 'I': '..', 'J': '.---',
            'K': '-.-', 'L': '.-..', 'M': '--', 'N': '-.', 'O': '---',
            'P': '.--.', 'Q': '--.-', 'R': '.-.', 'S': '...', 'T': '-',
            'U': '..-', 'V': '...-', 'W': '.--', 'X': '-..-', 'Y': '-.--', 'Z': '--..',
            '0': '-----', '1': '.----', '2': '..---', '3': '...--', '4': '....-',
            '5': '.....', '6': '-....', '7': '--...', '8': '---..', '9': '----.',
            '.': '.-.-.-', ',': '--..--', '?': '..--..', "'": '.----.', '!': '-.-.--',
            '/': '-..-.', '(': '-.--.', ')': '-.--.-', '&': '.-...', ':': '---...',
            ';': '-.-.-.', '=': '-...-', '+': '.-.-.', '-': '-....-', '_': '..--.-',
            '"': '.-..-.', '$': '...-..-', '@': '.--.-.', ' ': '/'
        }
        # 摩斯码到字符的反向映射
        self.morse_to_char = {v: k for k, v in self.char_to_morse.items()}

    def encrypt(self, text: str) -> str:
        """将普通文本加密为摩斯密码"""
        return ' '.join(
            self.char_to_morse.get(char.upper(), char) for char in text
        )

    def decrypt(self, morse_code: str) -> str:
        """将摩斯密码解密为普通文本"""
        # 用空格分割每个摩斯字符
        morse_list = morse_code.strip().split(' ')
        decoded_chars = []

        for code in morse_list:
            if code == '/':  # 单词分隔符
                decoded_chars.append(' ')
            else:
                decoded_chars.append(self.morse_to_char.get(code, code))  # 转换或保留原样

        return ''.join(decoded_chars)


if __name__ == "__main__":
    ciphertext = ".... . .-.. .-.. --- .-- .... .- - .. ... - .... . -.- . -.-- .. - .. ... -... --- --- .--. -... . . .--."
    decrypted = MorseCode().decrypt(ciphertext)
    print(f"解密: {ciphertext} → {decrypted}")

    # flag{HELLOWHATISTHEKEYITISBOOPBEEP}

2.15 [MRCTF2020]古典密码知多少

2.15.1 题目

2.15.2 解题思路

猪圈密码 + 圣堂武士密码 + 标准银河字母 + 栅栏密码（key=3）

2.15.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
# 猪圈密码 + 圣堂武士密码 + 标准银河字母 得到：fgcpflirtuasyon

import math

class Railfence:
    @staticmethod
    def encrypt(message, key=None):
        """
        加密函数：实现 Rail Fence Cipher 的分段加密。
        """
        if key is not None:
            ciphertext = ''
            for i in range(key):
                ciphertext += message[i::key]
            return ciphertext
        else:
            # 遍历 key 从 2 到 12
            results = {}
            for k in range(2, 13):
                ciphertext = ''
                for i in range(k):
                    ciphertext += message[i::k]
                results[k] = ciphertext
            return results

    @staticmethod
    def decrypt(ciphertext, key=None):
        """
        解密函数：根据密文和密钥 key 还原原文。
        """
        if key is not None:
            plaintext = ''
            row_length = math.ceil(len(ciphertext) / key)
            for i in range(row_length):
                plaintext += ciphertext[i::row_length]
            return plaintext
        else:
            # 遍历 key 从 2 到 16
            results = {}
            for k in range(2, 17):
                row_length = math.ceil(len(ciphertext) / k)
                plaintext = ''
                for i in range(row_length):
                    plaintext += ciphertext[i::row_length]
                results[k] = plaintext
            return results


if __name__ == '__main__':
    ciphertext = r"fgcpflirtuasyon"
    for i in range(2, 17):
        pt = Railfence.decrypt(ciphertext, i)
        if 'flag' in pt:
            print(f'flag{{{pt}}}')

            # flag{flagiscryptofun}

2.16 [WUSTCTF2020]佛说：只能四天

2.16.1 题目

1
2
3
4
5
6
7
8
9
# 题目描述.txt
圣经分为《旧约全书》和《新约全书》

# hint.txt
1. 虽然有点不环保，但hint好像是一次性的，得到后就没有利用价值了。
2. 凯撒不是最后一步，by the way，凯撒为什么叫做凯撒？

# 题目.txt
尊即寂修我劫修如婆愍闍嚤婆莊愍耨羅嚴是喼婆斯吶眾喼修迦慧迦嚩喼斯願嚤摩隸所迦摩吽即塞願修咒莊波斯訶喃壽祗僧若即亦嘇蜜迦須色喼羅囉咒諦若陀喃慧愍夷羅波若劫蜜斯哆咒塞隸蜜波哆咤慧聞亦吽念彌諸嘚嚴諦咒陀叻咤叻諦缽隸祗婆諦嚩阿兜宣囉吽色缽吶諸劫婆咤咤喼愍尊寂色缽嘚闍兜阿婆若叻般壽聞彌即念若降宣空陀壽愍嚤亦喼寂僧迦色莊壽吽哆尊僧喼喃壽嘚兜我空所吶般所即諸吽薩咤諸莊囉隸般咤色空咤亦喃亦色兜哆嘇亦隸空闍修眾哆咒婆菩迦壽薩塞宣嚩缽寂夷摩所修囉菩阿伏嘚宣嚩薩塞菩波吶波菩哆若慧愍蜜訶壽色咒兜摩缽摩諦劫諸陀即壽所波咤聞如訶摩壽宣咤彌即嚩蜜叻劫嘇缽所摩闍壽波壽劫修訶如嚩嘇囉薩色嚤薩壽修闍夷闍是壽僧劫祗蜜嚴嚩我若空伏諦念降若心吽咤隸嘚耨缽伏吽色寂喃喼吽壽夷若心眾祗喃慧嚴即聞空僧須夷嚴叻心願哆波隸塞吶心須嘇摩咤壽嘚吶夷亦心亦喃若咒壽亦壽囑囑

2.16.2 解题思路

新佛曰密码 + 社会主义核心价值观加密 + 栅栏密码（key=4） + 凯撒密码（key=3） + Base32

2.16.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
# http://www.pcmoe.net/article-89-1.html
# 新佛曰密码网站失效，等待后续开源，这里直接用前人的 wp 假装已经解出佛曰加密。

import re
import math
import random
import string
import base64
from urllib import parse
from typing import List
from typing import Optional


class ChineseCoreSocialistValues:
    VALUE = '富强民主文明和谐自由平等公正法治爱国敬业诚信友善'      # 映射的中文字符，每两个字符编码一个数值（0~15）

    @staticmethod
    def _to_url_hex(inp: str) -> str:
        """step1：将字符串转为 URL 编码后去掉 '%' 并转为大写十六进制"""
        reg = re.compile(r'[A-Za-z0-9\-\_\.\!\~\*\'\(\)]')
        # 非保留字符转换为十六进制，其它保留
        tmp = reg.sub(lambda g: hex(ord(g.group(0)))[2:], inp)
        return parse.quote(tmp).replace('%', '').upper()

    @staticmethod
    def _hex_to_int_sequence(hex_str: str) -> List[int]:
        """step2：将十六进制字符串转为整数序列（0~15），带编码标记"""
        result = []
        for c in hex_str:
            v = int(c, 16)
            if v < 10:
                result.append(v)
            elif random.random() < 0.5:
                result.extend([11, v - 6])  # 标记11：值为 v = x + 6
            else:
                result.extend([10, v - 10])  # 标记10：值为 v = x + 10
        return result

    @classmethod
    def _int_sequence_to_chinese(cls, seq: List[int]) -> str:
        """step3：将整数序列转为中文字符序列（每2字符表示1数值）"""
        return ''.join(cls.VALUE[v << 1] + cls.VALUE[v << 1 | 1] for v in seq)

    @classmethod
    def encrypt(cls, text: str) -> str:
        """完整加密过程：明文 -> URL Hex -> 编码序列 -> 中文"""
        hex_str = cls._to_url_hex(text)
        seq = cls._hex_to_int_sequence(hex_str)
        return cls._int_sequence_to_chinese(seq)

    @classmethod
    def _chinese_to_int_sequence(cls, enc: str) -> List[int]:
        """step6：中文密文转整数序列"""
        assert len(enc) % 2 == 0
        return [cls.VALUE.index(enc[i:i+2]) >> 1 for i in range(0, len(enc), 2)]

    @staticmethod
    def _int_sequence_to_hex(seq: List[int]) -> str:
        """step5：整数序列还原为十六进制字符串"""
        result = ''
        i = 0
        while i < len(seq):
            if seq[i] < 10:
                result += str(seq[i])
                i += 1
            elif seq[i] == 10:
                result += hex(seq[i + 1] + 10)[2:]
                i += 2
            elif seq[i] == 11:
                result += hex(seq[i + 1] + 6)[2:]
                i += 2
            else:
                raise ValueError(f'非法数据：{seq[i]}')
        return result

    @staticmethod
    def _hex_to_text(hex_str: str) -> str:
        """step4：十六进制字符串还原为明文"""
        percent_encoded = ''.join('%' + hex_str[i:i+2] for i in range(0, len(hex_str), 2))
        return parse.unquote(percent_encoded)

    @classmethod
    def decrypt(cls, enc: str) -> str:
        """完整解密过程：中文 -> 编码序列 -> hex -> 明文"""
        seq = cls._chinese_to_int_sequence(enc)
        hex_str = cls._int_sequence_to_hex(seq)
        return cls._hex_to_text(hex_str)


class Railfence:
    @staticmethod
    def encrypt(message, key=None):
        """
        加密函数：实现 Rail Fence Cipher 的分段加密。
        """
        if key is not None:
            ciphertext = ''
            for i in range(key):
                ciphertext += message[i::key]
            return ciphertext
        else:
            # 遍历 key 从 2 到 12
            results = {}
            for k in range(2, 13):
                ciphertext = ''
                for i in range(k):
                    ciphertext += message[i::k]
                results[k] = ciphertext
            return results

    @staticmethod
    def decrypt(ciphertext, key=None):
        """
        解密函数：根据密文和密钥 key 还原原文。
        """
        if key is not None:
            plaintext = ''
            row_length = math.ceil(len(ciphertext) / key)
            for i in range(row_length):
                plaintext += ciphertext[i::row_length]
            return plaintext
        else:
            # 遍历 key 从 2 到 16
            results = {}
            for k in range(2, 17):
                row_length = math.ceil(len(ciphertext) / k)
                plaintext = ''
                for i in range(row_length):
                    plaintext += ciphertext[i::row_length]
                results[k] = plaintext
            return results


class RotCipher:
    """ROT系列加密算法实现（支持ROT3/5/10/13/18/47/ROT-5/ROT-6）"""
    @staticmethod
    def _rotate_char(char: str, base: int, shift: int, range_size: int) -> str:
        """对单个字符进行指定偏移量的 ROT 加密/解密"""
        if not char.isspace():  # 跳过空白字符
            char_code = ord(char)
            if base <= char_code < base + range_size:
                # 计算旋转后的字符代码
                char_code = (char_code - base + shift) % range_size + base
            return chr(char_code)
        return char

    @staticmethod
    def shift_cipher(text: str, offset: int = None, alphabet: str = None) -> dict | str:
        """
        通用移位密码实现
        """
        if alphabet is None:
            # 默认使用标准字母表（大小写字母）
            alphabet_upper = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
            alphabet_lower = "abcdefghijklmnopqrstuvwxyz"
            
            if offset is not None:
                result = []
                for c in text:
                    if c.isupper():
                        idx = (alphabet_upper.index(c) + offset) % 26
                        result.append(alphabet_upper[idx])
                    elif c.islower():
                        idx = (alphabet_lower.index(c) + offset) % 26
                        result.append(alphabet_lower[idx])
                    else:
                        result.append(c)
                return ''.join(result)
            else:
                results = {}
                for o in range(1, 27):  # 字母表长度为26
                    results[o] = RotCipher.shift_cipher(text, o, alphabet)
                return results
        else:
            # 使用自定义字符表
            if offset is not None:
                result = []
                for c in text:
                    if c in alphabet:
                        idx = (alphabet.index(c) + offset) % len(alphabet)
                        result.append(alphabet[idx])
                    else:
                        result.append(c)  # 不在字符表中的字符保持不变
                return ''.join(result)
            else:
                results = {}
                for o in range(1, len(alphabet)):
                    results[o] = RotCipher.shift_cipher(text, o, alphabet)
                return results


class BaseXEncoder:
    # 常见进制的编码表
    STANDARD_TABLES = {
        16: b"0123456789ABCDEF",
        32: b"ABCDEFGHIJKLMNOPQRSTUVWXYZ234567",
        58: b"123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz",
        62: b"0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz",
        64: b"ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/",
        91: b"ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789!#$%&()*+,./:;<=>?@[]^_`{|}~\"",
        92: b"!\"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\\]^_`abcdefghijklmnopqrstuvwxyz{|}~",
        128: bytes(range(128)),  # 每个字节本身
    }

    def encode(self, data: bytes, base: int, table: Optional[bytes] = None, padding: Optional[bytes] = b"=") -> str:
        """
        编码函数：支持 base16, base32, base64, base58, base62, base91, base92, base128
        :param data: 待编码的原始字节数据
        :param base: 编码使用的进制
        :param table: 自定义编码表（可选）
        :param padding: 指定填充字符（如 b'='），传 None 表示不加填充
        """
        table = table or self.STANDARD_TABLES.get(base)

        # 标准 base 编码（内置支持填充）
        if base == 16:
            encoded = base64.b16encode(data).translate(bytes.maketrans(b"0123456789ABCDEF", table))
        elif base == 32:
            encoded = base64.b32encode(data).translate(bytes.maketrans(self.STANDARD_TABLES[32], table))
        elif base == 64:
            encoded = base64.b64encode(data).translate(bytes.maketrans(self.STANDARD_TABLES[64], table))
        elif base in (58, 62, 91, 92, 128):  # 自定义 baseX 编码
            return self._baseX_encode(data, table).decode("utf8")
        else:
            raise ValueError(f"Unsupported base: {base}")

        # 处理填充字符
        if padding is None:
            encoded = encoded.rstrip(b"=")
        elif padding != b"=":
            encoded = encoded.rstrip(b"=").replace(b"=", padding)

        return encoded.decode("utf8")

    def decode(self, ciphertext: str, base: int, table: Optional[bytes] = None, padding: Optional[bytes] = b"=") -> bytes:
        """
        解码函数：对应 encode 函数的逆过程
        :param ciphertext: 加密后的字符串
        :param base: 使用的进制
        :param table: 使用的编码表
        :param padding: 填充字符（如 b'='），传 None 表示密文无填充
        """
        encoded = ciphertext.encode("utf-8")
        table = table or self.STANDARD_TABLES.get(base)

        if base in (58, 62, 91, 92, 128):
            return self._baseX_decode(encoded, table)

        # 恢复 padding
        if padding is not None and padding != b"=":
            encoded = encoded.replace(padding, b"=")

        # 计算并自动补足 base32/base64 所需的 padding 长度
        def pad_base(data: bytes, block_size: int = 8) -> bytes:
            pad_len = (-len(data)) % block_size
            return data + b'=' * pad_len

        if base == 16:
            return base64.b16decode(encoded.translate(bytes.maketrans(table, b"0123456789ABCDEF")))
        elif base == 32:
            padded = pad_base(encoded)  # base32 长度必须为 8 的倍数
            return base64.b32decode(padded.translate(bytes.maketrans(table, self.STANDARD_TABLES[32])))
        elif base == 64:
            padded = pad_base(encoded, block_size=4)  # base64 长度必须为 4 的倍数
            return base64.b64decode(padded.translate(bytes.maketrans(table, self.STANDARD_TABLES[64])))
        else:
            raise ValueError(f"Unsupported base: {base}")

    def _baseX_encode(self, data: bytes, table: bytes) -> bytes:
        """
        自定义 baseX 编码（如 base58/base62）：将字节数据按目标进制编码为字符表中的字符序列
        """
        num = int.from_bytes(data, byteorder='big')
        base = len(table)
        encoded = bytearray()

        while num > 0:
            num, rem = divmod(num, base)
            encoded.insert(0, table[rem])

        # 前导 0 用 table[0] 表示
        pad = 0
        for b in data:
            if b == 0:
                pad += 1
            else:
                break

        return bytes([table[0]]) * pad + bytes(encoded)

    def _baseX_decode(self, encoded: bytes, table: bytes) -> bytes:
        """
        自定义 baseX 解码：将字符序列转换回原始字节数据
        """
        base = len(table)
        index = {char: i for i, char in enumerate(table)}
        num = 0
        for char in encoded:
            num = num * base + index[char]

        decoded = num.to_bytes((num.bit_length() + 7) // 8, byteorder='big')

        # 处理前导 0
        pad = 0
        for c in encoded:
            if c == table[0]:
                pad += 1
            else:
                break

        return b'\x00' * pad + decoded


if __name__ == "__main__":
    encoder = BaseXEncoder()
    ct = '平等文明自由友善公正自由诚信富强自由自由平等民主平等自由自由友善敬业平等公正平等富强平等自由平等民主和谐公正自由诚信平等和谐公正公正自由法治平等法治法治法治和谐和谐平等自由和谐自由自由和谐公正自由敬业自由文明和谐平等自由文明和谐平等和谐文明自由和谐自由和谐和谐平等和谐法治公正诚信平等公正诚信民主自由和谐公正民主平等平等平等平等自由和谐和谐和谐平等和谐自由诚信平等和谐自由自由友善敬业平等和谐自由友善敬业平等法治自由法治和谐和谐自由友善公正法治敬业公正友善爱国公正民主法治文明自由民主平等公正自由法治平等文明平等友善自由平等和谐自由友善自由平等文明自由民主自由平等平等敬业自由平等平等诚信富强平等友善敬业公正诚信平等公正友善敬业公正平等平等诚信平等公正自由公正诚信平等法治敬业公正诚信平等法治平等公正友善平等公正诚信自由公正友善敬业法治法治公正公正公正平等公正诚信自由公正和谐公正平等'
    dec1 = ChineseCoreSocialistValues.decrypt(ct)
    dec2 = Railfence.decrypt(dec1[:71])
    dec3 = RotCipher.shift_cipher(dec2[4][:55])
    flag = encoder.decode(dec3[23], 32, padding=b"=")
    print(flag)

    # b'wctf2020{ni_hao_xiang_xiang_da_wo}'

2.17 rot

2.17.1 题目

1
2
3
4
5
破解下面的密文：

83 89 78 84 45 86 96 45 115 121 110 116 136 132 132 132 108 128 117 118 134 110 123 111 110 127 108 112 124 122 108 118 128 108 131 114 127 134 108 116 124 124 113 108 76 76 76 76 138 23 90 81 66 71 64 69 114 65 112 64 66 63 69 61 70 114 62 66 61 62 69 67 70 63 61 110 110 112 64 68 62 70 61 112 111 112

flag格式flag{}

2.17.2 解题思路

ROT-13 + MD5 爆破

2.17.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
import hashlib
import itertools
from gmssl import sm3
from typing import Union


class RotCipher:
    """ROT系列加密算法实现（支持ROT3/5/10/13/18/47/ROT-5/ROT-6）"""
    @staticmethod
    def _rotate_char(char: str, base: int, shift: int, range_size: int) -> str:
        """对单个字符进行指定偏移量的 ROT 加密/解密"""
        if not char.isspace():  # 跳过空白字符
            char_code = ord(char)
            if base <= char_code < base + range_size:
                # 计算旋转后的字符代码
                char_code = (char_code - base + shift) % range_size + base
            return chr(char_code)
        return char
    
    @staticmethod
    def shift_cipher(text: str, offset: int = None, alphabet: str = None) -> dict | str:
        """
        通用移位密码实现
        """
        if alphabet is None:
            # 默认使用标准字母表（大小写字母）
            alphabet_upper = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
            alphabet_lower = "abcdefghijklmnopqrstuvwxyz"
            
            if offset is not None:
                result = []
                for c in text:
                    if c.isupper():
                        idx = (alphabet_upper.index(c) + offset) % 26
                        result.append(alphabet_upper[idx])
                    elif c.islower():
                        idx = (alphabet_lower.index(c) + offset) % 26
                        result.append(alphabet_lower[idx])
                    else:
                        result.append(c)
                return ''.join(result)
            else:
                results = {}
                for o in range(1, 27):  # 字母表长度为26
                    results[o] = RotCipher.shift_cipher(text, o, alphabet)
                return results
        else:
            # 使用自定义字符表
            if offset is not None:
                result = []
                for c in text:
                    if c in alphabet:
                        idx = (alphabet.index(c) + offset) % len(alphabet)
                        result.append(alphabet[idx])
                    else:
                        result.append(c)  # 不在字符表中的字符保持不变
                return ''.join(result)
            else:
                results = {}
                for o in range(1, len(alphabet)):
                    results[o] = RotCipher.shift_cipher(text, o, alphabet)
                return results


def hash_data(data: Union[bytes, str], algorithm: str, output_type: str = "hex", hash_length: int = None, hex_case: str = "lower") -> tuple:
    """
    计算数据的哈希值，支持多种算法和输出类型
    """
    # 统一转换为字节类型（兼容字符串输入）
    data_bytes = data.encode("utf-8") if isinstance(data, str) else data

    # 计算哈希值及长度
    match algorithm.lower():
        case "sha256" | "md5" | "sha1":
            hasher = hashlib.new(algorithm, data_bytes)
            digest = hasher.digest()
            original_length = hasher.digest_size

        case "sm3":
            hex_digest = sm3.sm3_hash(list(data_bytes))  # gmssl返回十六进制字符串
            digest = bytes.fromhex(hex_digest)           # 转换为字节
            original_length = 32                         # SM3固定32字节

        case _:
            raise ValueError(f"不支持的算法: {algorithm}（支持：sha256/md5/sha1/sm3）")

    # 长度控制
    if hash_length is not None:
        if not isinstance(hash_length, int) or hash_length <= 0:
            raise ValueError("hash_length必须是正整数")
        if hash_length > original_length:
            raise ValueError(f"长度超出限制（最大{original_length}字节）")
        digest = digest[:hash_length]  # 截断字节串
        actual_length = hash_length
    else:
        actual_length = original_length  # 不截断时使用原始长度

    # 转换输出类型
    match output_type.lower():
        case "bytes":
            result = digest
        case "hex":
            hex_str = digest.hex()
            # 十六进制大小写转换
            result = hex_str.upper() if hex_case.lower() == "upper" else hex_str.lower()
        case "int":
            result = int.from_bytes(digest, byteorder="big")
        case _:
            raise ValueError(f"不支持的输出类型: {output_type}（支持：bytes/hex/int）")

    return result, actual_length


if __name__ == "__main__":
    ct = [83, 89, 78, 84, 45, 86, 96, 45, 115, 121, 110, 116, 136, 132, 132, 132, 108, 128, 117, 118, 134, 110, 123, 111, 110, 127, 108, 112, 124, 122, 108, 118, 128, 108, 131, 114, 127, 134, 108, 116, 124, 124, 113, 108, 76, 76, 76, 76, 138, 23, 90, 81, 66, 71, 64, 69, 114, 65, 112, 64, 66, 63, 69, 61, 70, 114, 62, 66, 61, 62, 69, 67, 70, 63, 61, 110, 110, 112, 64, 68, 62, 70, 61, 112, 111, 112]
    res = ''.join(map(chr, ct))
    all_ascii_chars = ''.join(chr(i) for i in range(256))
    print(RotCipher.shift_cipher(res, -13, all_ascii_chars))
    # FLAG IS flag{www_shiyanbar_com_is_very_good_????}
    # MD5:38e4c352809e150186920aac37190cbc

    for chars in itertools.product(map(chr, range(32, 127)), repeat=4):
        m = 'flag{www_shiyanbar_com_is_very_good_' + ''.join(chars) + '}'
        des, _ = hash_data(m, 'md5')
        if '38e4c352809e150186920aac37190cbc' == des:
            print(m)
            break

        # flag{www_shiyanbar_com_is_very_good_@8Mu}

2.18 [MRCTF2020]天干地支+甲子

2.18.1 题目

1
2
3
4
5
6
7
8
9
得到得字符串用MRCTF{}包裹
一天Eki收到了一封来自Sndav的信，但是他有点迷希望您来解决一下
甲戌
甲寅
甲寅
癸卯
己酉 
甲寅
辛丑

2.18.2 解题思路

天干地支加密

2.18.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
import gmpy2
import itertools
from base64 import b64decode
from Crypto.Util.number import long_to_bytes, inverse, GCD, bytes_to_long


class tiangan_dizhi:
    ganzhi_dict = {
        1: "甲子", 2: "乙丑", 3: "丙寅", 4: "丁卯", 5: "戊辰",
        6: "己巳", 7: "庚午", 8: "辛未", 9: "壬申", 10: "癸酉",
        11: "甲戌", 12: "乙亥", 13: "丙子", 14: "丁丑", 15: "戊寅",
        16: "己卯", 17: "庚辰", 18: "辛巳", 19: "壬午", 20: "癸未",
        21: "甲申", 22: "乙酉", 23: "丙戌", 24: "丁亥", 25: "戊子",
        26: "己丑", 27: "庚寅", 28: "辛卯", 29: "壬辰", 30: "癸巳",
        31: "甲午", 32: "乙未", 33: "丙申", 34: "丁酉", 35: "戊戌",
        36: "己亥", 37: "庚子", 38: "辛丑", 39: "壬寅", 40: "癸卯",
        41: "甲辰", 42: "乙巳", 43: "丙午", 44: "丁未", 45: "戊申",
        46: "己酉", 47: "庚戌", 48: "辛亥", 49: "壬子", 50: "癸丑",
        51: "甲寅", 52: "乙卯", 53: "丙辰", 54: "丁巳", 55: "戊午",
        56: "己未", 57: "庚申", 58: "辛酉", 59: "壬戌", 60: "癸亥"
    }
    reverse_dict = {v: k for k, v in ganzhi_dict.items()}

    @classmethod
    def decrypt(cls, ganzhi_list):
        """
        将干支列表转换为对应的数字列表
        """
        result = []
        for item in ganzhi_list:
            if item in cls.reverse_dict:
                result.append(cls.reverse_dict[item])
            else:
                raise ValueError(f"无效的干支字符串: {item}")
        return result

    @classmethod
    def encrypt(cls, number_list):
        """
        将数字列表转换为对应的干支列表
        """
        result = []
        for num in number_list:
            if 1 <= num <= 60:
                result.append(cls.ganzhi_dict[num])
            else:
                raise ValueError(f"数字超出范围 (1-60): {num}")
        return result
    

if __name__ == "__main__":
    encrypted = tiangan_dizhi.decrypt(["甲戌", "甲寅", "甲寅", "癸卯", "己酉", "甲寅", "辛丑"])
    msg1 = "".join([chr(i + 60) for i in encrypted])
    print(msg1)

    # flag{Goodjob}

2.19 [NCTF2019]Keyboard

2.19.1 题目

1
ooo yyy ii w uuu ee uuuu yyy uuuu y w uuu i i rr w i i rr rrr uuuu rrr uuuu t ii uuuu i w u rrr ee www ee yyy eee www w tt ee

2.19.2 解题思路

九键键盘密码（特点：字母组合中每组字符位数为 1 至 4 位不等）

2.19.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def T9_password(cipher: str) -> str:
    """
    解码 T9 九键密码（支持数字或字母输入）
    """
    table = [" ", " ", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"]
    base = " qwertyuiop"
    result = []

    for part in cipher.split():
        key_index = int(part[0]) if part.isdigit() else base.index(part[0])
        char_index = len(part) - 1
        if 0 <= key_index < len(table) and char_index < len(table[key_index]):
            result.append(table[key_index][char_index])

    return ''.join(result)


if __name__ == "__main__":
    ct = "ooo yyy ii w uuu ee uuuu yyy uuuu y w uuu i i rr w i i rr rrr uuuu rrr uuuu t ii uuuu i w u rrr ee www ee yyy eee www w tt ee"
    m = T9_password(ct)
    print(f'flag{{{m}}}')

    # flag{youaresosmartthatthisisjustapieceofcake}

2.20 [MRCTF2020]vigenere

2.20.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# cipher.txt
g vjganxsymda ux ylt vtvjttajwsgt bl udfteyhfgt
oe btlc ckjwc qnxdta 
vbbwwrbrtlx su gnw nrshylwmpy cgwps, lum bipee ynecgy gk jaryz frs fzwjp, x puej jgbs udfteyhfgt, gnw sil uuej su zofi. sc okzfpu bl lmi uhzmwi, x nyc dsj bl lmi enyl ys argnj yh nrgsi. nba swi cbz ojprbsw fqdam mx. cdh nsai cb ygaigroysxn jnwwi lr msylte.
cw mekr tg jptpzwi kdikjsqtaz, ftv pek oj pxxkdd xd ugnj scr, yg n esqxwxw nba onxw au ywipgkj fyiuujnxn gnss xwnz onxw jnahl avhwwxn vzkjpu nrofch fvwfoh. v jwhppek lmi vyutfp hbiafp hcguj at nxw gyxyjask ib hw seihxsqpn vtvjttajwsx ds zzj xnegfsmtf egz wtrq lt mbcukj sc hy. qty wnbw ss bbxsq vxtnl ys ghrw zw cbx vt cdh vgxwtfy ssc brzzthh bl wsjdeiwricg cw mekr zjzi grgktr ib lwfv.
vbbwwrbrtlx hteonj xwroj oyhg vgbigf ljtq iuk utrhrtl tj iuk ytztetwi. cdh nsai crolmig fudngxgkv ssg ekujmkrj gzvh. jk vnh cbz aszxgk qty. nba vt rdg qfta jf, tgw hd lum prdj umw aderv. hcqrxkuerr jgjw cbz dni lvzznr nbaj gsgqkjx. hd aul ylxaq lmei lum hec oaaqh xg, gk yldhmz nx lrxw f tjorah gdaylwyrgogs tgbpwhx. nba ufrcbz. ay mh nt shx ds tsyygr gfi mi txgbw xgywqj iuxgzkw baj hsaykuymkr guymday.
qty wnbw ssi rtyfktq of tyg txwfx paj yfxwrxask rbtnjvhnzatr, cbx vnh nba uwipgk lmi lrgdyl ds umw qpeqwytaniwx. cdh jg ssi xtgb sje imqxjek, gzv tgnahw, de zzj ycjxayxta igiih gnsy eaeksic eeunnht baj xsrvkld qdek gwhte zzfr rbadi ft bhlfmcrj td ecl ux dsje oeushvzatrh.
lum hppvs lmigr gjj tgbhdjqh nsgsk jf zzfx nba fjis gu ktpkr. egz yhr zznw rygar eh nt wcgjfk lt mcigvj sje vjjgxailx. qpae gk xwryw uvdorwrw sbt'l jbxfz. omigr zzjvt nxw wipy igsjavilx, awrxw yltek swi leuflw, lr caqp xqkfymul zzjq paj sihgryk yltz hq tyg zkssw. lr gjj jdesask dhx gbr hbiafp rbtlwerg. zznw vbbwwrpaiw bmay gjnwt niutvsvty ys iuk utrsvzatrh bl gzv lbxdi, rdg egzvh. baj bsgyj ax hxslwwicg.
iqgigfvshi rbtknwif ux yvpayshxxbtk, wianzatrhuohx, ecq zztyvuz aywtyl, swvplkv qmzr g kyecqofl apik as xwr cwg su baj hsbzafngpgogsw. dhxk nw p jujqh iugl nw qbzz jzteeomigr gfi rdjnwwi, qhz ay mh aul bltek tthxry dnzt.
jk swi reksymct g otvaq zzfx pyr efc tazww axgngzx eeonnpttk gw tgrpmimrr guhsgqkv gc gniw, jgdaueng ebcww, qxyolfvn sujhi, de ylfxxbt gk fxezz.
bi pek uwipgofl e lbxdi awrxw frnbtw, frnjnwwi bne wctgryk mmh bx zjv qrrajjh, au efxirx zta hvtyzppe, cayldhz xjeg bl tjmct igjvrrj asxd fodjrrr uj hscsujrmil.
egzv armsq gdaiwuxh bl hwserxld, imcxwxwxbt, aiicgold, qdikejri, ntv hscgkpy hd aul fteye lt yh. gnwd egr gdq fpfkv tr bnzljv, paj lmigr ok ss bnzljv wrxw.
tyg vjwsxxgowx lpik ft fdqowx, wd, htdnot lum, bi rntftx dozsnr dejww fn cnqxmrnr utigpogs. at okdnikr zzfx ueue jxwvik, jravmzyicrj kjpu-vtljvtfz, ssh iuk utqbbtojea, baj lskrxffrrr caqp tzkjli. dhx aiicgolnih zgq gi svylwmqhzwi ereukx qpae gk cdhx bzvxfjahxxbtk. ylt btdd ppj zzfx pyr gzv rbtkymihkfy gjyzmwih jumqh vrtwweaye jjgdttaei xf zzj kdyjws vjyk. oj ldck oj axyr tj eqyk lt fjvrv tyg cgjymrhrsw wdyalnscf uf ylpg hsxmh. oal bi rntftx ppiwux iuk ktpjgogsw nba swi pgzwrtivty ys xzvgxi.
xa zzj ycvzwi winzwx, cdh nsai ibjsd ggrgljh p ygo, ylt gkdjgdzsmsmrnzatrh ekxtvb nil, blxpn jjtjqosyih lumw sla igswivzmymda gfi mcfadyw iuk vwipzy gk ntslwwwda, csxlxamltr, bvrd, resvygs, htguizikvrdj, ecq hjfrsrok. yltfk vwipzy ezwi auo gi qbxf frtj of zw.
nba swi irxjnjxrj gk cdhx gbr ruodivta, yasgt gnwd egr tsymkry as e lbxdi awrxw dsj jodq eajgqx ft vsenkgntlx. ftpgmxi nba xjeg gnwr, cdh kfyvjfz qtyg oajjejpxshmtf cayl iuk hfvtazsq vtfvgswxoodnxxry qty pek lts rbcswhal zg hscsxgsx nbajxiaikk. nr dhx otvaq, gdq xwr ywsxxzkfyw paj wctgryknscf ux mybntayc, ueue ylt qktfwxam lt xwr gfliavi, swi enxlx su n ywfqaryk bldyk, lmi vyutfp rbtnjvhnzatr ds hayw. lr issrdg ywuegnzw ylt noj ylpg iztotf ljtq iuk snv jcuf blxpn onrvf hwfx.
xa iznrp, tkjrecl, ljfrrr, xmxwxn, yaskpcujj, minrq frs gnw zrxgkv xxpgkk, dsj nxw yvnvty ys lnxv tju gnw amghy gk pxokjyc ql kjjgivty lypej htwif gl ylt sxgsxxrxk tj rlhwwweniw. yltfk efc zrkh tyi gnw hscggynsc suj f wbnrd ymbr, hmy xwre onpa aul bsgx of f aderv ylpg caqp hbuf gi qygfpiirj as fxg-hwfvxam ejhxn.
egzv xaijjehvtyqc doygqiir ofksgzglnsc vtvzwieowx adhrv uigcklzeir zzjqhrrnjw ql vjttdfofl ppjy, as ebrxahe paj wqwtjnwwi, iugl hppvs lt sla yhjiru olxias zzwsjtngzx iuk otvaq. zzjwt ygox adhrv iirygjj msrgk ys qr gftxwrx ashjfzjnea cxgiyrg, tg rsgr tggpt gnss txt ojtr. xa umw aderv, blpgknjv iuk zzqpa sash bne uwipgk ufr qr xwuvdqaujh paj vnwieotzxtq ofkmcvzwqc pg tg hshg. zzj kabhsq gdabwdecpk gk xwbaymx cb rgskte xwvyxekk dsje lshxdeowx xd niutqeyokm.
xwryw nrreksxmctrq mshgodj ecq igqscvgd ripfajjw eyguj yh vt lmi hnsw ushvzatr pf zztwt cxwamdhy dtztey gk jgrkvtq paj kjpu-qkljvbvtsymda czt lpq zg wiyril ylt nalmsgvzajw ds jaxxpaz, msmcsujris cuojvh. jk ezwi qkuqegr umw zxezmfp hrrnjw xzsmsi ib egzv hbbwwixttld, ikrt sx at pufymchk lt gdaywsx ib egzv ghrw tzte umw fdqowx. at jodq weeksi sjeywqztf guwshf zzj tantwy wd gnsy rd btw hec nxjjwi baj yldhmzyw.
lr caqp reksyi p ponnpxmglnsc bl lmi bvtv nr rlhwwweniw. ren vz tj qdek zzqpak ssh unoj ylpa zzj aderv dsje mgaigaswsxh ugnj qpqk tjjdek.
xqev vy ewgis balicrxw hvnczg hvppq efr, eyksxi pqj mshteyutvt ntv hygye twerry.


# vigenere.txt
from ctf import source_text, key_string

getdiff = lambda char: ord(char)-ord('a')
getchar = lambda num: chr(ord('a')+num)

def vigenere(src: chr, key: chr) -> chr:
    assert(src.isalpha() and key.isalpha())
    return(getchar((getdiff(src) + getdiff(key) + 1) % 26))

src = source_text.lower()
count = 0
assert(len(key_string) > 5 and len(key_string) < 10)
for i in src:
    if(i.isalpha()):
        print(vigenere(i, key_string[count % len(key_string)]), end='')
        count+=1
    else:
        print(i, end='')

2.20.2 解题思路

无密钥维吉尼亚密码

2.20.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
import re
import requests
from parsel import Selector
from fake_useragent import UserAgent


def VigenereWithoutKey(ciphertext):
    headers = {
        'accept': 'text/html,application/xhtml+xml,application/xml;q=0.9,image/avif,image/webp,image/apng,*/*;q=0.8,application/signed-exchange;v=b3;q=0.7',
        'content-type': 'application/x-www-form-urlencoded',
        'origin': 'https://guballa.de',
        'referer': 'https://guballa.de/vigenere-solver',
        'sec-ch-ua': '"Chromium";v="136", "Microsoft Edge";v="136", "Not.A/Brand";v="99"',
        'user-agent': UserAgent().random,
    }

    response = requests.get('https://guballa.de/vigenere-solver', headers=headers)
    selector = Selector(text=response.text)
    unique_form_id = selector.xpath('//input[@name="__unique_form_id__"]/@value').get()
    form_nonce = selector.xpath('//input[@name="form-nonce"]/@value').get()

    data = {
        'data[ciphertext]': ciphertext,
        'data[variant]': 'vigenere',
        'data[language]': 'en',
        'data[keylength]': '3-30',
        '__form-name__': 'vig-breaker',
        '__unique_form_id__': unique_form_id,
        'form-nonce': form_nonce
    }

    response = requests.post('https://guballa.de/vigenere-solver', headers=headers, data=data)
    selector = Selector(text=response.text)

    key_text = selector.xpath('//*[@id="body-wrapper"]/section/div/div[2]/div[1]/p/text()').get()
    plaintext = selector.xpath('//*[@id="body-wrapper"]/section/div/div[2]/textarea/text()').get()

    key_match = re.search(r'"(.*?)"', key_text or "")
    key = key_match.group(1) if key_match else None
    return {
        'key': key,
        'decrypted': plaintext
    }
    
if __name__ == "__main__":
    with open(r'cipher.txt', 'r', encoding="utf8") as f:
        vigenere_cipher = f.read()
    print(VigenereWithoutKey(vigenere_cipher))

    # ...flag is mrctf vigenere crypto crack man...
    # flag{vigenere_crypto_crack_man}

2.21 [MRCTF2020]keyboard

2.21.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
得到的flag用
MRCTF{xxxxxx}形式上叫
都为小写字母

6
666
22
444
555
33
7
44
666
66
3

2.21.2 解题思路

九键键盘密码

2.21.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def T9_password(cipher: str) -> str:
    """
    解码 T9 九键密码（支持数字或字母输入）
    """
    table = [" ", " ", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"]
    base = " qwertyuiop"
    result = []

    for part in cipher.split():
        key_index = int(part[0]) if part.isdigit() else base.index(part[0])
        char_index = len(part) - 1
        if 0 <= key_index < len(table) and char_index < len(table[key_index]):
            result.append(table[key_index][char_index])

    return ''.join(result)


if __name__ == "__main__":
    ct_number = "6 666 22 444 555 33 7 44 666 66 3"
    m_number = T9_password(ct_number)
    print(f'flag{{{m_number}}}')

    # flag{mobilephond}

2.22 一张谍报

2.22.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 家能源总部经过派出卧底长期刺探，终于找到一个潜伏已久的国外内鬼：三楼能源楼管老王。由于抓捕仓促，老王服毒自尽了。侦查部门搜出老王每日看的报纸原来是特制的情报。聪明的你能从附件的报纸中找出情报么？flag是老王说的暗号。（由于老王的线人曾今做的土匪，所以用的行话）

国家能源时报2015年3月5日
平时要针对性的吃些防辐射菜
对于和电脑“朝夕相处”的人们来说,辐射的确是个让人忧心的“副产物”。因此,平时针对性的吃些可以防辐射的菜是很有好处的。特别是现在接近年底，加班加点是家常便饭，对着电脑更是辐射吸收得满满的，唯有趁一日三餐进食的时候吃点防辐射的食物了。

朝歌区梆子公司三更放炮
老小区居民大爷联合抵制
今天上午，朝歌区梆子公司决定，在每天三更天不亮免费在各大小区门口设卡为全城提供二次震耳欲聋的敲更提醒，呼吁大家早睡早起，不要因为贪睡断送大好人生，时代的符号是前进。为此，全区老人都蹲在该公司东边树丛合力抵制，不给公司人员放行，场面混乱。李罗鹰住进朝歌区五十年了，人称老鹰头，几年孙子李虎南刚从东北当猎户回来，每月还寄回来几块鼹鼠干。李罗鹰当年遇到的老婆是朝歌一枝花，所以李南虎是长得非常秀气的一个汉子。李罗鹰表示：无论梆子公司做的对错，反正不能打扰他孙子睡觉，子曰：‘睡觉乃人之常情’。梆子公司这是连菩萨睡觉都不放过啊。李南虎表示：梆子公司智商捉急，小心居民猴急跳墙！这三伏天都不给睡觉，这不扯淡么！
到了中午人群仍未离散，更有人提议要烧掉这个公司，公司高层似乎恨不得找个洞钻进去。直到治安人员出现才疏散人群归家，但是李南虎仍旧表示爷爷年纪大了，睡不好对身体不好。

朝歌区梆子公司三更放炮
老小区居民大爷联合抵制
喵天上午，汪歌区哞叽公司决定，在每天八哇天不全免费在各大小区门脑设卡为全城提供双次震耳欲聋的敲哇提醒，呼吁大家早睡早起，不要因为贪睡断送大好人生，时代的编号是前进。为此，全区眠人都足在该公司流边草丛合力抵制，不给公司人员放行，场面混乱。李罗鸟住进汪歌区五十年了，人称眠鸟顶，几年孙叽李熬值刚从流北当屁户回来，每月还寄回来几块报信干。李罗鸟当年遇到的眠婆是汪歌一枝花，所以李值熬是长得非常秀气的一个汉叽。李罗鸟表示：无论哞叽公司做的对错，反正不能打扰他孙叽睡觉，叽叶：‘睡觉乃人之常情’。哞叽公司这是连衣服睡觉都不放过啊。李值熬表示：哞叽公司智商捉急，小心居民猴急跳墙！这八伏天都不给睡觉，这不扯淡么！
到了中午人群仍未离散，哇有人提议要烧掉这个公司，公司高层似乎恨不得找个洞钻进去。直到治安人员出现才疏散人群归家，但是李值熬仍旧表示爷爷年纪大了，睡不好对身体不好。

听书做作业

喵汪哞叽双哇顶，眠鸟足屁流脑，八哇报信断流脑全叽，眠鸟进北脑上草，八枝遇孙叽，孙叽对熬编叶：值天衣服放鸟捉猴顶。鸟对：北汪罗汉伏熬乱天门。合编放行，卡编扯呼。人离烧草，报信归洞，孙叽找爷爷。

2.22.2 解题思路

单表替换密码：单表替换，可见两段重复新闻内容略有差异，对比提取不同之处组成翻译表，还原明文。

2.22.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
if __name__ == "__main__":
    flag=""
    str1="今天上午，朝歌区梆子公司决定，在每天三更天不亮免费在各大小区门口设卡为全城提供二次震耳欲聋的敲更提醒，呼吁大家早睡早起，不要因为贪睡断送大好人生，时代的符号是前进。为此，全区老人都蹲在该公司东边树丛合力抵制，不给公司人员放行，场面混乱。李罗鹰住进朝歌区五十年了，人称老鹰头，几年孙子李虎南刚从东北当猎户回来，每月还寄回来几块鼹鼠干。李罗鹰当年遇到的老婆是朝歌一枝花，所以李南虎是长得非常秀气的一个汉子。李罗鹰表示：无论梆子公司做的对错，反正不能打扰他孙子睡觉，子曰：‘睡觉乃人之常情’。梆子公司这是连菩萨睡觉都不放过啊。李南虎表示：梆子公司智商捉急，小心居民猴急跳墙！这三伏天都不给睡觉，这不扯淡么！到了中午人群仍未离散，更有人提议要烧掉这个公司，公司高层似乎恨不得找个洞钻进去。直到治安人员出现才疏散人群归家，但是李南虎仍旧表示爷爷年纪大了，睡不好对身体不好。"
    str2="喵天上午，汪歌区哞叽公司决定，在每天八哇天不全免费在各大小区门脑设卡为全城提供双次震耳欲聋的敲哇提醒，呼吁大家早睡早起，不要因为贪睡断送大好人生，时代的编号是前进。为此，全区眠人都足在该公司流边草丛合力抵制，不给公司人员放行，场面混乱。李罗鸟住进汪歌区五十年了，人称眠鸟顶，几年孙叽李熬值刚从流北当屁户回来，每月还寄回来几块报信干。李罗鸟当年遇到的眠婆是汪歌一枝花，所以李值熬是长得非常秀气的一个汉叽。李罗鸟表示：无论哞叽公司做的对错，反正不能打扰他孙叽睡觉，叽叶：‘睡觉乃人之常情’。哞叽公司这是连衣服睡觉都不放过啊。李值熬表示：哞叽公司智商捉急，小心居民猴急跳墙！这八伏天都不给睡觉，这不扯淡么！到了中午人群仍未离散，哇有人提议要烧掉这个公司，公司高层似乎恨不得找个洞钻进去。直到治安人员出现才疏散人群归家，但是李值熬仍旧表示爷爷年纪大了，睡不好对身体不好。"
    str3="喵汪哞叽双哇顶，眠鸟足屁流脑，八哇报信断流脑全叽，眠鸟进北脑上草，八枝遇孙叽，孙叽对熬编叶：值天衣服放鸟捉猴顶。鸟对：北汪罗汉伏熬乱天门。合编放行，卡编扯呼。人离烧草，报信归洞，孙叽找爷爷。"
    
    diff_dict = {}
    for c1, c2 in zip(str1, str2):
        if c1 != c2:
            diff_dict[c2] = c1

    print(''.join(diff_dict.get(c, c) for c in str3))
    
    # flag{南天菩萨放鹰捉猴头}

2.23 [AFCTF2018]Vigenère

2.23.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include <stdio.h>
#include <string.h>
#include <stdlib.h>

int main()
{
	freopen("flag.txt","r",stdin);
	freopen("flag_encode.txt","w",stdout);
	char key[] = /*SADLY SAYING! Key is eaten by Monster!*/;
	int len = strlen(key);
	char ch;
	int index = 0;
	while((ch = getchar()) != EOF){
		if(ch>='a'&&ch<='z'){
			putchar((ch-'a'+key[index%len]-'a')%26+'a');
			++index;
		}else if(ch>='A'&&ch<='Z'){
			putchar((ch-'A'+key[index%len]-'a')%26+'A');
			++index;
		}else{
			putchar(ch);
		}
	}
	return 0;
}


# flag_encode.txt
Yzyj ia zqm Cbatky kf uavin rbgfno ig hnkozku fyyefyjzy sut gha pruyte gu famooybn bhr vqdcpipgu jaaju obecu njde pupfyytrj cpez cklb wnbzqmr ntf li wsfavm azupy nde cufmrf uh lba enxcp, tuk uwjwrnzn inq ksmuh sggcqoa zq obecu zqm Lncu gz Jagaam aaj qx Hwthxn'a Gbj gfnetyk cpez, g fwwang xnapriv li phr uyqnvupk ib mnttqnq xgioerry cpag zjws ohbaul drinsla tuk liufku obecu ovxey zjwg po gnn aecgtsneoa.

Cn poyj vzyoe gxdbhf zq ty oeyl-ndiqkpl, ndag gut mrt cjy yrrgcmd rwwsf, phnz cpel gtw yjdbcnl bl zjwcn Cekjboe cklb yeezjqn htcdcannhum Rvmjlm, phnz juoam vzyoe nxn Tisk, Navarge jvd gng honshoc wf Ugrhcjefy. — Cpag zq kyyuek cpefk taadtf, Mxdeetowhps nxn qnfzklopeq gvwnt Sgf, xarvbrvg gngal fufz ywwrxu xlkm gnn koaygfn kf gnn ooiktfyz, — Tugc ehrtgnyn aae Owrz uh Yireetvmng hguiief jnateaelcre bl cpefk gfxo, ig ob bhr Xkybp os zqm Prurdy po nrcmr bx vg uxoyobp ig, gpv nk iaycqthzg fys Gbbnznzkpl, fwyvtp qtf lqmhzagoxv oa ywub lrvtlqpyku shz oemjvimopy cps cufmrf op koyh suau, af zq lbam fnjtl fkge gksg rrseye vg ybfric bhrot Kubege jvd Ugrhcjefy. Yzuqkpuy, enqknl, wvrn vcytnzn bhnz Igparasnvtf rqfa asggktifngv mdohrm vog hg ubwntkm noe rkybp aaj czaaykwhp cnabms; ntf swyoejrvgye cdf axckaqeaig zuph fnnen gncl gwnxowl aek ogla dvyywsrj vg mqfska, ehvrg wpelf gam shlhwlwbyk cpaa zq jcchg zqmmfknnyo bl gkwlvyjahc tuk owrzy vg qdipn cpel gtw uychycwmrj. Dmn shrt j toam vjuen bl jjufku shz ufaaxagoqfm, lueydqnt opnuninhug tuk usga Oopnkt rbkfwas n jnaitt vg ladhin bhrs wfxar nhbwlhzg Vyopbzram, vz kk ndevx aqguz, kl co tukrz dhza, li pheuf wfs ywub Coikavmrtv, shz tb vawvvjg fys Ghgals sut lbaie ldbuek uwwqrvzh. — Aupn jsm xert cpe cgvayjt faoneegpuy kf gnnae Pungheef; gwl shij am joj zqm nrigkmetl cqqcu iqfmprnowa tuko li wlgka bhrot xinmrx Bgsgkok ib Gbbnznzkpl. Nde uobboee qx nde cxnaeaz Mahc os Mamag Htanwia ob i hvyvglu os xnxenzgv cjjhxrms ntf mmqrcgcqoay, cdf daiowo ia jkjyyt bhsmcg zjw yotnhuqsusgfn kf nt jjsbrwly Pyegwvy bbgj ndefk Bbagku. Li lrbbn bhvy, nwn Bapzb je fadecptrj cw a pgpvcz wbxul.

Hr nck lafhynl hvy Ckmang zx Tajy, vzy iofz fpoykugga aaj wmcryuslu fbx cpe caddcy gbum.

Pe ugu xinbvjmmn uou Yireetxzs gu rsmo Lncb wf vsowxeagk jvd cxgkment ovxoezcfwa, uarnas fauhyjdrj rv tukkj ileegcqoa zkdf dif Gbaeaz uziqlq hn wbggkfyz; aaj fpea yq kooprtmmd, uk jsm qtgkaty akidyytrj cw agzgfx po gnnu.

Hr nck lafhynl tb vckm ktuka Tajy hgl phr glkozsqvupibt xn lnxiw xesgxrktf uh hykpyk, dvlryu lbksr vnwpyk ygohd ekuqndakkb phr xrohg uh Jylrrynvtnzkgh en gnn Tetoudupuek, j zitnv ahasgovibyk vg ndez gwl fbxoaxwbyk cw tlxcfno oarh.

Pe ugu uuhlrj cwgrzjwl hetobtagoxw vkdvkb it crcuyo uaabcay, apuiifbxcibyk, cfx zifzjvt sxqe nde qkywsvzqjs kf gnnqr Caddcy Rrixzdf, lqj nde fuum phxrgma os ljbitakfa phrs rvtb iqejhintlm wvzj zco mrgbcrry.

Jw bws qobaoybgv Lapekbmnggvapa Hbabms ekrwupeqrh, noe urhioiam fqtu scffu fvxvvefy jam enigbqoay qf nde eopptf uh lba pruyte.

Uk jsm nesabmd sut s fknt zrue, nlvwl oupn mqsfunmneoay, cw cnauw iphrxb bo ok gdyytrj, fpeekdq nde Ykpqsygvapa Pbcnzs, vtesjwbyk xn Aatkzchagoxv, hnbg jypuetnl tb zjw Jaocrn it ygtyy boe zqmie kzwlyifk; cpe Fzcly nezgrviam kf nde zkjv tvsg wrlofkm bo nrn lba dntpmrf uh ahrafoxv feuo ocphbac, inq iqfpqlfoxvs jovzcj.

Hr nja eajgspkuekm bo cxgnyjt gnn xocansneoa uo bhryg Knwtry; owr gncl jqrcubm ooyvjoytvtp bhr Rcom boe Tjbuegnatwtvuw wf Sutwccnrxb; zesauahc tb vjas bzjwlo tb kwkohxcyy phroa uitxclcknf nrbhrx, cfx navyrvg gng uijdvzrwnf uh fys Acvawpeoclcknf uo Taaju.

Zy daf ukateaelyz tuk Jlmvtkknnagoxv os Pwknecr hh zesauahc hvy Jasrtv li Hajy owr ryvsvhifnrvg Wafaweaee Ywwrxu.

Zy daf sjle Wafyyo drvnvdrtv gh dif Crtl nrqfy boe zqm trtwjy kf gnnqr blhawas, ntm bhr gogojt ntm xalsgfn kf gnnqr fgnsleef.

luig vy cxwpf{Jnxwobuqg_O_Cogiqi!}

Hr nck ynepznl a zanlcpuqk xn Nrc Qxzecry, jvd fkpl betuka awnxok ib Oslrkeey vg bwrnyb wue vggjhe ntm mag uwl ndevx bcbfzcfwa.

Hr nja krvv sgknt ab, qn goowm kf ckjke, Fzcfxent Gauiry yandohz cpe Pupkyjt bl xcr ykiamhagaams.

Uk jsm wfsklbeq zq jyjdrx cpe Zonanwrl owleckpvyjt bl jvd farwleoe zx bhr Iknch Pbcnz.

Hr nck wkmoowmd jovz iphrxb bo fadbyyt hy cw a watamzipzrwn sutwccn gu xcr pupknethzrwn, ntf mhwcxtxelrjiwx xy baa tajy; iapent nra Afygfn po gnnqr Nivk ib pekcmnqkf Dycifrjbibt:

Hgl munxcmrvti dungr hxliry qx unmrj czobvu sgknt ab:

Noe vtgnacgowo tuko, ts w mbit Brvgn xlkm cawqsusgfn boe gwg Mhxfwlo wuolp tuka kbkuyj lwmzov gh phr Owpaoovshps bl cpefk Ulupef:

Lxz chzvahc osl xcr Gxcvy sign jtl cgtlm kf gnn eoerf:

Xin izvxaiam Vsras bt da wvzjgop ohx Lwnfkpl:

Zkr qkyziiopy oo ia sjvy pguwm, kf gnn jeakhan kf Gxril oe Lmlu:

Fbx czaayrglpiam da breqfx Oeny cw br ztayz fbx yzegkpvyz oslnvcry:

Hgl wbbrrahvti lba fekn Ayfzge ib Eamuqsu Rcom en n tnqguhqmlent Vawvvtew, yotnhuqsuopy ndeekrv aa Gttcprnxh ooiktfgang, gwl earcjaent oca Bbapvuniry bw af zq jyjdrx rb ag upuy wn rdjupyk cfx big owateaowhp fbx rvteufmwent zqm snsg svooyacm rhrg ahpo gnnae Pungheef

Lxz tnqkfa wwne xcr Pncjnarf, gkwlvyjahc ohx vwsg bcdowbyk Uiwf gpv uhtrxrvg sapvuieazjtll zjw Zkrzy xn ohx Igparasnvtf:

Lqj mqsckwliam qml kwa Rnoifrclonef, gwl drinslent zqmmfknnyo iabnatrj yand pbcnz tb rgycolnzn noe au ah wly ijaef cjsnoorbnz.

Hr nck uxdvijbeq Mqnynnzkwb hrxg, ts zeprjziam wk iqt bl qqs Cxqlyytvuw inq ccycjg Jga ignopkn qs.

Uk qis crwfxarrj xcr fkck, lwvnmnl ohx eguotf, hdzng uwj nkway, jvd qkullkyrj cpe yoxwm kf baa xebvnw.

Ba if gc bhvy vaga tegwapbxvahc lnxpm Aeskwm kf suamitt Owlyeagaqef zq uiipykjb tuk yglgs bl mmagn, fwmklnzrwn, ntf lsnaath, ilekcvs xetaw eign ealyuzycinpku gz Yrhkuby & Cktxczy fijzcrra hunayrnteq op lba mbyc jaehcjiqs nmna, aaj vgnwlye dvwbxvzs phr Nnid bl c ucriyoimd agvaij.

Hr nja cbtullwiakm wue lgdfkw Pocqzrtu lugea Ijxtvbg gh phr nroh Fkck nk brga Irzy cyuenfz cpevx Egojtee, cw briqey phr kgmchzkgharf uo bhrot xleeajb inq Htwndrrt, xz tb lcdf phrsbmliku ts phroa Paaju.

Zy daf kgkigkf viiefzrk iaywjlacgoxvs nsqfaot hy, jvd ugu whzenbxcrrj vg vniam xv tuk kfbwbvzjvtf uh gon feuwbirxu, lba mrxlqlryu Ahzint Bivnmgk qdofk tvojt tmfa os cjzfnxg, am wn htmqsgopyoesukm lefztmwpibt xn ayr cyyo, srdna aaj eghzigoxvs.

Vt gnyny fzjoe bl vzyoe Bvyzefykgho Wr njde Ckvaneoakm noe Xgvlasf ow bhr sqkn duzhum trxok: Iqr ekymagkf Hypigoxvs ugxw vaea gwawrxgv ijll hh zeckclyz iapdzy. N Vtahye, jnxae pncjuytrx ra tuau eunkrj kg eiktq uyt jnrkh zga vybiak j Byegpl, co ualrb tb hg lba rhrnz os g hjya pruyte.

Aut zure Jk kmea ccfnent ow itgkplcknf zx wue Htanesu hamtuxgf. Qa hnbn eaetgv ndez lawm goow nk tvsn wf nzvwgltf hh bhrot dycifrjbuek vg yttrtm in htyslnaazjjlr pwjcodvicqoa uxwl qs. Jk qivr xgecjdrj cpez uh lba cvxlcmfzcfwas bl xcr rskylwtvuw inq yglnhezkwb hrxg. Oy daik jxprgnwx po gnnqr agvapa jhycqcr gpv gwgagwqmvza, shz wr njde pupboneq zqmm oe vzy piry xn ohx eggioa qrvdekf li zifgeww gngky qshxyitvupk, qdipn fwuyj kfyriggkty vtvwlnucz xcr pupfyytvuwa aaj eglnefvxvdrtew. Ndel zxw hnbg tyan qkjn tb zjw pkipk xn jhyvawa aaj xn cbtushcuvtrby. Jk ommp, tukamfbxg, swmuvkbke vt vzy jepkbaige, yzcyh qkwwuaigk iqr Fkyirnzkgh, wnq nxtd gnge, uo wr nxtd gng jyot bl vinxopv, Yjezona ia Ccj, cj Prglm Feogfxo.

Wr, zqmrrlqjy, phr Xnxrrygfnwtvbna os zjw ojigkm Atnzgk ib Azkaqcn, op Yyjeegu Koamtwmo, Afynubykf, sjlenrrvg gu vzy Oucxnue Wafyy kf gnn eoerf xin tuk amcgovmxa os udz iazgfneoay, mw, ia zjw Hwmr, gwl bl Gwlbkrvzh wf gng yikd Ckxxlr uh lbasr Ixtoaogk, mklrswty caddcoh ntm leprcjy, Phnz cpefk wfcpeq Ixtoaogk une, ntm wf Eoizn kutnc bo ok Hjya aaj Rvdrvgfxang Ycitry, vzup tukh irr Gdkihvrj ozoz gnd Uhlrmrinpk vg nde Oxrbifn Ejisn, ntm bhnz cdf loyocqcnr eghjepzrwn okvoyan gnnu aaj vzy Otnzn wf Txgsn Xrvzjqn, vy cfx kutnc bo ok vgnwlye mqsfunnyz; aaj cpag gu Xlae ntm Qnqkrwhzeaz Bbagku, lbay ugem fhrn Hisee zx teie Ysl, yoaiucdr Vgswa, cbtczapz Cdfeaaina, efzctfesu Ixumrxew, ujd gu mw ayr qlbar Nica aaj Vzcjgf cqqcu Opvyleajnvt Fzclyo mne xn rvmjl xk. — Aaj owr gng kolpbxc wf gnkk Xacygaitvup, ocph n lrzm eknaujcr uw bhr vtgnacgoxv os Jkncje Cxxdiqkpuy, se zaccayra hfadtk cw enij gndee udz Lvbgk, iqr Suabuaku, shz ohx bicekf Zijoe.

2.23.2 解题思路

无密钥维吉尼亚密码

2.23.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
import re
import requests
from parsel import Selector
from fake_useragent import UserAgent


def VigenereWithoutKey(ciphertext):
    results = {}

    headers = {
        'accept': 'text/html,application/xhtml+xml,application/xml;q=0.9,image/avif,image/webp,image/apng,*/*;q=0.8,application/signed-exchange;v=b3;q=0.7',
        'content-type': 'application/x-www-form-urlencoded',
        'origin': 'https://guballa.de',
        'referer': 'https://guballa.de/vigenere-solver',
        'sec-ch-ua': '"Chromium";v="136", "Microsoft Edge";v="136", "Not.A/Brand";v="99"',
        'user-agent': UserAgent().random,
    }

    response = requests.get('https://guballa.de/vigenere-solver', headers=headers)
    selector = Selector(text=response.text)
    unique_form_id = selector.xpath('//input[@name="__unique_form_id__"]/@value').get()
    form_nonce = selector.xpath('//input[@name="form-nonce"]/@value').get()

    data = {
        'data[ciphertext]': ciphertext,
        'data[variant]': 'vigenere',
        'data[language]': 'en',
        'data[keylength]': '3-30',
        '__form-name__': 'vig-breaker',
        '__unique_form_id__': unique_form_id,
        'form-nonce': form_nonce
    }

    response = requests.post('https://guballa.de/vigenere-solver', headers=headers, data=data)
    selector = Selector(text=response.text)

    key_text = selector.xpath('//*[@id="body-wrapper"]/section/div/div[2]/div[1]/p/text()').get()
    plaintext = selector.xpath('//*[@id="body-wrapper"]/section/div/div[2]/textarea/text()').get()

    key_match = re.search(r'"(.*?)"', key_text or "")
    key = key_match.group(1) if key_match else None
    return {
        'key': key,
        'decrypted': plaintext
    }
    
if __name__ == "__main__":
    with open(r'flag_encode.txt', 'r', encoding="utf8") as f:
        vigenere_cipher = f.read()
    print(VigenereWithoutKey(vigenere_cipher))

    # ...flag is afctf{Whooooooo_U_Gotcha!}\n\nHe has...
    # afctf{Whooooooo_U_Gotcha!}

2.24 [AFCTF2018]Single

2.24.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <bits/stdc++.h>
using namespace std;
int main()
{
	freopen("Plain.txt","r",stdin);
	freopen("Cipher.txt","w",stdout);
	map<char, char> f;
	int arr[26];
	for(int i=0;i<26;++i){
		arr[i]=i;
	}
	random_shuffle(arr,arr+26);
	for(int i=0;i<26;++i){
		f['a'+i]='a'+arr[i];
		f['A'+i]='A'+arr[i];
	}
	char ch;
	while((ch=getchar())!=EOF){
		if(f.count(ch)){
			putchar(f[ch]);
		}else{
			putchar(ch);
		}
	}
	return 0;
}


Jmqrida rva Lfmz (JRL) eu m uqajemf seny xl enlxdomrexn uajiderc jxoqarerexnu. Rvada mda rvdaa jxooxn rcqau xl JRLu: Paxqmdyc, Mrrmjs-Yalanja mny oekay.

Paxqmdyc-urcfa JRLu vmu m jxiqfa xl giaurexnu (rmusu) en dmnza xl jmrazxdeau. Lxd akmoqfa, Wab, Lxdanuej, Jdcqrx, Benmdc xd uxoarvenz afua. Ramo jmn zmen uxoa qxenru lxd atadc uxftay rmus. Oxda qxenru lxd oxda jxoqfejmray rmusu iuimffc. Rva nakr rmus en jvmen jmn ba xqanay xnfc mlrad uxoa ramo uxfta qdatexiu rmus. Rvan rva zmoa reoa eu xtad uio xl qxenru uvxwu cxi m JRL wenad. Lmoxiu akmoqfa xl uijv JRL eu Yaljxn JRL gimfu.

Waff, mrrmjs-yalanja eu mnxrvad enradaurenz seny xl jxoqarerexnu. Vada atadc ramo vmu xwn narwxds(xd xnfc xna vxur) werv tifnmdmbfa uadtejau. Cxid ramo vmu reoa lxd qmrjvenz cxid uadtejau mny yatafxqenz akqfxeru iuimffc. Ux, rvan xdzmnehadu jxnnajru qmdrejeqmnru xl jxoqarerexn mny rva wmdzmoa urmdru! Cxi uvxify qdxrajr xwn uadtejau lxd yalanja qxenru mny vmjs xqqxnanru lxd mrrmjs qxenru. Veurxdejmffc rveu eu m ledur rcqa xl JRLu, atadcbxyc snxwu mbxir YAL JXN JRL - uxoarvenz fesa m Wxdfy Jiq xl mff xrvad jxoqarerexnu.

Oekay jxoqarerexnu omc tmdc qxuuebfa lxdomru. Er omc ba uxoarvenz fesa wmdzmoa werv uqajemf reoa lxd rmus-bmuay afaoanru (a.z. IJUB eJRL).

JRL zmoau xlran rxijv xn omnc xrvad muqajru xl enlxdomrexn uajiderc: jdcqrxzdmqvc, urazx, benmdc mnmfcueu, datadua anzanaadenz, oxbefa uajiderc mny xrvadu. Zxxy ramou zanadmffc vmta urdxnz useffu mny akqadeanja en mff rvaua euuiau.

Iuimffc, lfmz eu uxoa urdenz xl dmnyxo ymrm xd rakr en uxoa lxdomr. Akmoqfa mljrl{Xv_I_lxiny_er_neja_rDc}

2.24.2 解题思路

随机替换密码：使用 http://quipqiup.com/ 词频分析。

2.24.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
import requests
import urllib3

# 忽略 SSL 证书警告
urllib3.disable_warnings(urllib3.exceptions.InsecureRequestWarning)

def decrypt_with_quipqiup(ciphertext: str, clues: str= "") -> dict:
    """
    使用 quipqiup.com 对替换加密密文进行自动解密。
    """
    headers = {
        "Accept": "*/*",
        "Accept-Language": "zh-CN,zh;q=0.9,en;q=0.8,en-GB;q=0.7,en-US;q=0.6",
        "Content-type": "application/x-www-form-urlencoded",
        "Origin": "http://quipqiup.com",
        "Referer": "http://quipqiup.com/",
        "User-Agent": "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/136.0.0.0 Safari/537.36 Edg/136.0.0.0",
    }

    payload = {
        "ciphertext": ciphertext,
        "clues": clues,
        "mode": "auto",
        "was_auto": True,
        "was_clue": False,
    }

    # 请求提交密文以开始解密
    try:
        response = requests.post("http://quipqiup.com/solve", headers=headers, json=payload, verify=False)
        response.raise_for_status()
        id_payload = {"id": response.json().get("id")}
    except Exception as e:
        print("提交解密请求失败:", e)
        return {}

    # 请求获取解密结果
    try:
        response = requests.post("http://quipqiup.com/status", headers=headers, json=id_payload, verify=False)
        response.raise_for_status()
        solutions = response.json().get("solutions", [])
    except Exception as e:
        print("获取解密结果失败:", e)
        return {}

    # 组织解密结果
    result = {}
    for s in solutions:
        result[s["key"]] = s["plaintext"]
    return result


if __name__ == '__main__':
    with open(r"Cipher.txt", 'r') as f:
        ct = f.read()
    result = decrypt_with_quipqiup(ct)
    for key, text in result.items():
        if 'afctf' in text:
            print(f"Key: {key}\nPlaintext: {text}\n")

            # afctf{Oh_U_found_it_nice_tRy}

2.25 [UTCTF2020]basic-crypto

2.25.1 题目

1
01010101 01101000 00101101 01101111 01101000 00101100 00100000 01101100 01101111 01101111 01101011 01110011 00100000 01101100 01101001 01101011 01100101 00100000 01110111 01100101 00100000 01101000 01100001 01110110 01100101 00100000 01100001 01101110 01101111 01110100 01101000 01100101 01110010 00100000 01100010 01101100 01101111 01100011 01101011 00100000 01101111 01100110 00100000 01110100 01100101 01111000 01110100 00101100 00100000 01110111 01101001 01110100 01101000 00100000 01110011 01101111 01101101 01100101 00100000 01110011 01101111 01110010 01110100 00100000 01101111 01100110 00100000 01110011 01110000 01100101 01100011 01101001 01100001 01101100 00100000 01100101 01101110 01100011 01101111 01100100 01101001 01101110 01100111 00101110 00100000 01000011 01100001 01101110 00100000 01111001 01101111 01110101 00100000 01100110 01101001 01100111 01110101 01110010 01100101 00100000 01101111 01110101 01110100 00100000 01110111 01101000 01100001 01110100 00100000 01110100 01101000 01101001 01110011 00100000 01100101 01101110 01100011 01101111 01100100 01101001 01101110 01100111 00100000 01101001 01110011 00111111 00100000 00101000 01101000 01101001 01101110 01110100 00111010 00100000 01101001 01100110 00100000 01111001 01101111 01110101 00100000 01101100 01101111 01101111 01101011 00100000 01100011 01100001 01110010 01100101 01100110 01110101 01101100 01101100 01111001 00101100 00100000 01111001 01101111 01110101 00100111 01101100 01101100 00100000 01101110 01101111 01110100 01101001 01100011 01100101 00100000 01110100 01101000 01100001 01110100 00100000 01110100 01101000 01100101 01110010 01100101 00100000 01101111 01101110 01101100 01111001 00100000 01100011 01101000 01100001 01110010 01100001 01100011 01110100 01100101 01110010 01110011 00100000 01110000 01110010 01100101 01110011 01100101 01101110 01110100 00100000 01100001 01110010 01100101 00100000 01000001 00101101 01011010 00101100 00100000 01100001 00101101 01111010 00101100 00100000 00110000 00101101 00111001 00101100 00100000 01100001 01101110 01100100 00100000 01110011 01101111 01101101 01100101 01110100 01101001 01101101 01100101 01110011 00100000 00101111 00100000 01100001 01101110 01100100 00100000 00101011 00101110 00100000 01010011 01100101 01100101 00100000 01101001 01100110 00100000 01111001 01101111 01110101 00100000 01100011 01100001 01101110 00100000 01100110 01101001 01101110 01100100 00100000 01100001 01101110 00100000 01100101 01101110 01100011 01101111 01100100 01101001 01101110 01100111 00100000 01110100 01101000 01100001 01110100 00100000 01101100 01101111 01101111 01101011 01110011 00100000 01101100 01101001 01101011 01100101 00100000 01110100 01101000 01101001 01110011 00100000 01101111 01101110 01100101 00101110 00101001 00001010 01010100 01101101 01010110 00110011 01001001 01000111 01001110 01101111 01011001 01010111 01111000 01110011 01011010 01010111 00110101 01101110 01011010 01010011 01000101 01100111 01010001 00110010 01000110 01110101 01001001 01001000 01101100 01110110 01100100 01010011 01000010 01101101 01100001 01010111 01100100 00110001 01100011 01101101 01010101 01100111 01100010 00110011 01010110 00110000 01001001 01001000 01100100 01101111 01011001 01011000 01010001 01101110 01100011 01111001 01000010 01101110 01100010 00110010 01101100 01110101 01011010 01111001 01000010 01110110 01100010 01101001 01000010 01101111 01011010 01011000 01001010 01101100 01010000 01111001 01000010 01001010 01100100 01000011 01000010 01110011 01100010 00110010 00111001 01110010 01100011 01111001 01000010 01110011 01100001 01010111 01110100 01101100 01001001 01001000 01010010 01101111 01011010 01010011 01000010 01110011 01011010 01011000 01010010 00110000 01011010 01011000 01001010 01111010 01001001 01000111 01000110 01111001 01011010 01010011 01000010 01111010 01100001 01000111 01101100 01101101 01100100 01000111 01010110 01101011 01001001 01000111 01001010 00110101 01001001 01001000 01001110 01110110 01100010 01010111 01010101 01100111 01011001 00110010 00111001 01110101 01100011 00110011 01010010 01101000 01100010 01101110 01010001 01110101 01001001 01000011 01101000 01101111 01100001 01010111 00110101 00110000 01001111 01101001 01000010 00110101 01100010 00110011 01010101 01100111 01100010 01010111 01101100 01101110 01100001 01001000 01010001 01100111 01100100 00110010 01000110 01110101 01100100 01000011 01000010 00110000 01100010 01111001 01000010 01111010 01100100 01000111 01000110 01111001 01100100 01000011 01000010 01110011 01100010 00110010 00111001 01110010 01100001 01010111 00110101 01101110 01001001 01001000 01010110 01110111 01001001 01000110 01001010 01110110 01100010 01010111 01000110 01110101 01001001 01001000 01000010 01101100 01100010 00110011 01000010 01110011 01011010 01010011 01101011 01110101 01000011 01101101 01110100 00110010 01011001 01101110 01001110 01111000 01100011 01101101 01010001 01110011 01001001 01000111 01101100 00110101 01011010 01010011 01100100 01101001 01100010 01111001 01000010 01110010 01100100 01101110 01100100 00110101 01011001 00110010 01010001 01100111 01011010 01001000 01001010 01110110 01011001 01101101 00111000 01101000 01001001 01000110 01101000 00110101 01011010 01111001 01000010 01110111 01100101 01010111 01001001 01100111 01011010 01001000 01001010 01110110 01001001 01001000 01000010 01111010 01100101 01000111 01110100 00110010 01001001 01000011 01101000 01110010 01100101 01000111 00110100 01100111 01100100 00110010 01110100 01110000 01100010 01000111 00111000 01100111 01011010 01001000 01001010 01110110 01001001 01001000 01001010 01110010 01011001 01101101 00110101 01110110 01011001 00110010 01010001 01110101 01001100 01101001 00110100 01110000 01001001 01001000 01110000 01110010 01011001 01101101 01010001 00110110 01001001 01000111 01110011 01100111 01011001 00110010 01010110 01110011 01011001 00110010 01010010 01111010 01011010 01000111 01010110 01101011 01100011 00110011 01101100 00110100 01001001 01000111 00110001 01111010 01100101 01101110 01001010 01110110 01011001 01101001 00110100 01100111 01010101 00110011 01100111 01100111 01011010 01001000 01001010 01110110 01001001 01001000 01000010 00110101 01100100 01101110 01011010 00110101 01011010 00110011 01001110 00110100 01100011 01010011 01000010 01101011 01100010 00110010 01101000 01101011 01001100 01000011 01000010 01010100 01001010 00110010 01011010 01110110 01001001 01000111 01010010 01110010 01100100 01010111 00111001 00110100 01001001 01001000 01100100 01110000 01001001 01001000 01100100 01110110 01011001 00110010 01001110 01110010 01100011 01010111 00111000 01100111 01100001 00110011 01101000 01110101 01001001 01000111 01001010 01110110 01100101 01101110 01011010 01110010 01100010 01010111 00111001 01110101 01001001 01000111 00111001 01101101 01100010 00110010 01001010 01110000 01001001 01000111 01110100 00110010 01100101 01101110 01001010 01110010 01100010 01000111 00111001 01101011 01100011 00110010 00110000 01100111 01100010 01011000 01001010 01110010 01011001 01101101 01110100 01110100 01011010 01000111 00111001 01101001 01001001 01000111 01100100 01111010 01011010 01001000 01001001 01100111 01100001 01111001 01000010 01110100 01100101 01010111 01001010 01101001 01100010 00110010 01001110 00110110 01100101 01011000 01101000 01110101 01100010 00110011 01101000 01110100 01100010 01111001 01000010 01101011 01100101 01010011 01000010 01110010 01001001 01000111 00110101 01111010 01100011 01001000 01000010 01110110 01011001 01101101 00111001 00110100 01011010 01000011 01000010 01110100 01100011 01101101 01110100 01101001 01100001 00110010 00110001 01101011 01100010 00110010 01001001 01100111 01001100 01010011 01000010 00110001 01100101 01001000 01101100 01101110 01100101 01000011 01000010 01110010 01011001 01111001 01000010 01110010 01001001 01000111 01001110 01101100 01100010 01000111 01001110 01101011 01100011 00110010 01010010 01101100 01011010 01001000 01001110 00110101 01100101 01000011 01000010 01110100 01100011 00110011 01110000 01111001 01100010 00110010 01001001 01110101 01001001 01000101 00110001 01110010 01100101 01000011 01000010 01110000 01100101 01010111 01010101 01100111 01100011 01001000 01001110 00110100 01100010 01101001 01000010 01101011 01100011 01101101 00111000 01100111 01100011 01001000 01001110 00110100 01100001 00110011 01011001 01100111 01100011 01001000 01011010 01110010 01100011 01010100 00111000 01100111 01100011 01101110 01001110 00110100 01011010 01000100 01101111 01100111 01010010 00110010 00111000 01100111 01100100 01011000 01101000 00110101 01011010 01111001 01000010 01101011 01100011 01101101 01110100 01101011 01001001 01000111 01010010 01111001 01100010 01111001 01000010 01110111 01100100 01101101 01110100 01111000 01001001 01001000 01001110 01101010 01001001 01001000 01000110 00110101 01100011 00110011 01101000 01111000 01001001 01000111 01010010 00110101 01001001 01000111 01111000 01110110 01001001 01001000 01101100 01110111 01001001 01000111 01010010 01111001 01100010 01111001 01000010 01110111 01100101 01010111 01001010 00110011 01100001 00110010 01010001 01100111 01011010 01010111 01010010 01110111 01100100 01101101 01110100 01111000 01100101 01111001 00110100 01110101 01001100 01101110 00110000 01100111 01001100 01010011 01000010 01101110 01100011 01101110 01001110 01110100 01100011 01101001 01000010 00110011 01100010 00110010 01110100 00110100 01011001 01111001 01000010 01101011 01100011 01101101 01110100 01101011 01001001 01001000 01001110 01110111 01001001 01000111 01101100 00110101 01011010 01010011 01000010 01101010 01100010 00110010 00111000 01100111 01011010 01001000 01001010 01110010 01011010 01000011 01000010 00110110 01100001 00110010 01010010 01101011 01100010 00110010 01001010 00110100 01001100 01000011 01000010 01110000 01100101 01010111 01010101 01100111 01100100 01011000 01101000 00110101 01011010 01111001 01000010 01101110 01100011 01101101 01110100 01101011 01001001 01000111 01010010 01111001 01100010 01111001 01000010 01110100 01100101 01010111 01001010 01101001 01100010 00110010 01001110 00110110 01100101 01011000 01101000 01110101 01100010 00110011 01101000 01110100 01100010 00110010 01001101 01100111 01100011 01001000 01101100 01101001 01001001 01000111 01010101 01110011 01001001 01000111 01010001 01110011 01001001 01001000 01000001 01110011 01001001 01001000 01011001 01100111 01100001 01111001 01110111 01100111 01100001 00110011 01101000 01110101 01001001 01001000 01000101 01100111 01100001 00110010 01001010 01110110 01001100 01101001 01000010 01001010 01100101 01010111 01010101 01100111 01100010 01010111 01110100 00110100 01001001 01001000 01110000 01101001 01100101 01010111 01111000 01110010 01100010 01001000 01011010 01110000 01001001 01000111 01100100 00110101 01011001 01101110 01010101 01100111 01100101 01010111 01010110 01101011 01001001 01000111 01010010 01111001 01100010 01111001 01000010 01101001 01100010 00110011 01100100 01110010 01100011 00110011 01101000 01111010 01100101 01001000 01000101 01100111 01100010 01011000 01001010 01110010 01011001 01101101 01110100 01110100 01011010 01000111 00111001 01101001 01011001 01111001 01000010 01110011 01100001 01010011 01000010 01101001 01100010 00110011 01110000 00110010 01100001 00110010 00110001 01111010 01100101 01001000 01000101 01100111 01011010 01001000 01001010 01110110 01100100 01111001 01000010 01110010 01100101 01000111 00110100 01100111 01100011 00110011 01101000 01110111 01100010 00110010 01001010 01101001 01100011 00110011 01101000 01111000 01001001 01000111 00110001 00110101 01100100 00110011 01100100 00110101 01100101 01000011 01000010 01101110 01100101 01010111 01001010 01110101 01011001 01111001 01000010 01111010 01100101 01000011 01000010 01101011 01100011 01101101 00111000 01100111 01010100 00110011 01101000 01111000 01100100 01101110 01001110 01101010 01100011 01101001 01000010 00110010 01100001 00110011 01101000 01111000 01011010 01010111 01110100 01111000 01100010 01111001 00110100 01100111 01010011 00110011 01101000 00110101 01011010 01001000 01001010 01110110 01011001 01101001 01000010 01111000 01011001 01101101 00111001 01110010 01011010 01000011 01000010 00110011 01100010 00110010 01010010 01111001 01100101 01010111 00110100 01100111 01100011 00110010 01001101 01100111 01011010 01001000 01101011 01100111 01011010 01010111 01001110 01110110 01001001 01001000 01000010 01101001 01100010 00110010 01000110 01101100 01100010 00110011 01101000 01110100 01100001 01010011 01000010 01110010 01100101 01000111 01110100 00110010 01100001 01010111 01001110 01111010 01011001 01111010 01101111 01100111 01011010 00110010 00111000 01100111 01100100 01011000 01101000 00110101 01011010 01111001 01000010 01101011 01100011 01101101 01110100 01101011 01001001 01000011 01100100 01110110 01001010 01111001 01000010 01101010 01100011 01101110 01101100 01101110 01011001 01111001 01000010 01101100 01100101 01101001 01000010 00110011 01100101 01010111 01001110 01101011 01001001 01001000 01101100 01110111 01011010 01000111 00111001 00110100 01001001 01001000 01001110 00110100 01001001 01000111 01010010 01111001 01100010 01111001 01000010 01110010 01100100 01101110 01110000 01111001 01100001 00110010 01111000 01110110 01011010 01000011 01110111 01100111 01011001 00110011 01101011 01100111 01011010 01001000 01001010 01110010 01011010 01000011 01100100 01101010 01001001 01001000 01110000 01101001 01100101 01010111 01111000 01110010 01100010 01001000 01011010 01110000 01001001 01000111 01010010 01111001 01100010 01111001 01000010 00110011 01100101 01010111 01001110 01101011 01001001 01000111 00110001 00110101 01100100 00110011 01100100 00110101 01100101 01000011 01000010 01110100 01100011 01101101 01110100 01101001 01100001 00110010 00110001 01101011 01100010 00110010 01001001 01100111 01100011 00110011 01100111 01100111 01011010 01001000 01001010 01110110 01001001 01000111 01010010 01110110 01100001 01000111 01010001 01110011 01001001 01001000 01000010 00110101 01100100 01101110 01011010 00110101 01011010 00110010 00111001 01110101 01001001 01000111 01111000 01110000 01001001 01000011 01100100 01101011 01001010 01111001 01110111 01100111 01100001 00110011 01101000 01110101 01001001 01000111 01001110 00110101 01001001 01001000 01101100 00110100 01001100 01101001 01000010 01011010 01100101 01000111 00110001 01110110 01001001 01000111 01101100 00110101 01011010 01010011 01000010 00110001 01100101 01001000 01101100 01101110 01001001 01000111 01110011 01100111 01100011 01000111 00111001 01101110 01001001 01000111 00110001 01111001 01100001 00110010 01001010 01110010 01100010 01010111 01010010 01110110 01011001 01101101 01001101 01110011 01001001 01000111 01101100 00110101 01011010 01010011 01000010 01110100 01100001 00110011 01100111 01100111 01100011 00110011 01101000 01110111 01100010 00110010 01001001 01100111 01011010 01001000 01001010 01110110 01001001 01000111 01001010 01110110 01011001 00110010 01010001 01100111 01100101 01011000 01000001 01100111 01011010 01001000 01001010 01110110 01001001 01000111 01100100 00110101 01011001 01101101 00110101 01101010 01001001 01000111 01111000 01110010 01011001 00110010 00111001 01110101 01001001 01001000 01101100 00110100 01001001 01000111 00110001 00110101 01100100 00110011 01100100 00110101 01100101 01000011 01000010 01101110 01100101 01010111 01001010 01110101 01011001 01111001 01000010 01101011 01100011 01101101 01110100 01101011 01001001 01000111 01001110 01111001 01100101 01010111 01100011 01100111 01011010 01011000 01101111 01100111 01100011 00110011 01100111 01100111 01011010 01001000 01001010 01110110 01001001 01000101 00111001 00110100 01100011 01011000 01011010 01111010 01011001 00110011 01001001 01100111 01100100 01101101 01110100 00110100 01100011 01010111 01010110 01110010 01100011 01010111 00111000 01110101 01000011 01101110 01001010 01101110 01100001 01000111 00110101 00110100 01100011 00110010 01010010 01101101 01100101 01011000 01001110 01101011 01100100 01000111 01100100 01101111 01100100 01010011 01000101 01100111 01100011 01010111 01100100 01101101 01001001 01000111 01101100 01111010 01011001 01010111 01110011 01100111 01011001 00110011 01010010 01101111 01100100 01001000 01010110 01110000 01100001 00110010 01010101 01100111 01011010 01000111 01101100 01110010 01001001 01001000 01110000 01110010 01100010 01101110 01010010 01101111 01100001 01000111 01110100 00110100 01001001 01001000 01001010 00110100 01100011 01010111 01111000 01101011 01011010 00110010 00110101 00110100 01100011 00110010 01111000 01110000 01100011 01010011 01000010 01111001 01100001 01011000 01001110 00110101 01100101 01010111 01110100 01101111 01100010 01101101 01110011 01110101 01001001 01000111 01101100 01110010 01100101 01000111 01110011 01100111 01100100 01001000 01010101 01100111 01100011 01111001 01000010 01101010 01100101 01011000 01001110 01110101 01001001 01000111 01001110 01101110 01100101 01000011 01000010 01111010 01100101 01011000 01101011 01100111 01100011 01010111 01100100 01101101 01100101 01000011 01000010 01110000 01100011 00110011 01101000 01101100 01001001 01000111 01110100 01101010 01011001 00110010 01100100 00110100 01011010 01001000 01010101 00110110 01001001 01000111 01011010 01101011 01011001 00110011 01101100 01111010 01100010 01101110 01110100 01101111 01001101 01001000 01011010 01100110 01011010 01000111 01101011 00110000 01011010 01001000 01010110 01100110 01100100 01101101 01101011 00110000 01011010 01000110 00111001 00110000 01011000 00110011 01001001 00110000 01100101 01011000 01101100 01100110 01100011 01101110 01101000 01111000 01100010 01000111 01010001 01110111 01100110 01010011 00110100 01100111 01100011 01010111 01100100 01101101 01001001 01001000 01011010 00110000 01100101 01011000 01101011 01100111 01011001 00110011 01010010 01101111 01011010 01010011 01000010 01101011 01100001 01011000 01001110 01101011 01001001 01001000 01001101 01100111 01100101 01010111 01100100 01101011 01001001 01000111 01100100 01101010 01001001 01001000 01001010 00110100 01100011 01010111 01111000 01101011 01011010 00110010 00110101 00110100 01100011 00110010 01111000 01110000 01100011 01010011 01000010 00110000 01100100 01010011 01000010 01110111 01011010 01101110 01010110 01101011 01001001 01001000 01110000 01101101 01100100 01001000 01101100 01101100 01100100 01000111 01101000 01110101 01001001 01000111 01100100 01101010 01011001 01111001 01000010 01101011 01100001 01011000 01010010 00110001 01001001 01001000 01010110 01101110 01100101 01000111 01010001 01100111 01011010 00110010 01001101 01100111 01100101 01101110 01001110 00110001 01100100 01001000 01001001 01100111 01011001 01101101 01101000 01101110 01100100 01101110 01101100 01110010 01011010 01010111 00110101 01110010 01001100 01000011 01000010 01111010 01100001 01000111 01010101 01100111 01100100 01000111 01010001 01100111 01100101 01000111 01110100 01111010 01100101 01011000 01101100 01111000 01001001 01001000 01010010 00110001 01001001 01000111 01101000 01101110 01011010 01000011 01000010 00110001 01011010 01111001 01000010 00110110 01100011 00110010 01010101 01100111 01100011 00110010 01001110 01101011 01100001 00110011 01100111 01100111 01100011 00110011 01101100 00110101 01001100 01101001 01000010 01110000 01011010 00110010 01111000 01110010 01001001 01001000 01000110 01101110 01011010 01101001 01000010 01110010 01100001 01001000 01000010 01101110 01100011 01010111 01110100 01101100 01001001 01000111 01010010 01110000 01100001 01111001 01000010 01111001 01100001 01011000 01001110 00110101 01100101 01010111 01110100 01101111 01100010 01101101 01110011 01101000

2.25.2 解题思路

二进制编码 + Base64 编码 + Avocat 密码（key=10） + 随机替换密码

2.25.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
from base64 import b64decode
import requests
import urllib3


# 忽略 SSL 证书警告
urllib3.disable_warnings(urllib3.exceptions.InsecureRequestWarning)


def decrypt_with_quipqiup(ciphertext: str, clues: str= "") -> dict:
    """
    使用 quipqiup.com 对替换加密密文进行自动解密。
    """
    headers = {
        "Accept": "*/*",
        "Accept-Language": "zh-CN,zh;q=0.9,en;q=0.8,en-GB;q=0.7,en-US;q=0.6",
        "Content-type": "application/x-www-form-urlencoded",
        "Origin": "http://quipqiup.com",
        "Referer": "http://quipqiup.com/",
        "User-Agent": "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/136.0.0.0 Safari/537.36 Edg/136.0.0.0",
    }

    payload = {
        "ciphertext": ciphertext,
        "clues": clues,
        "mode": "auto",
        "was_auto": True,
        "was_clue": False,
    }

    # 请求提交密文以开始解密
    try:
        response = requests.post("http://quipqiup.com/solve", headers=headers, json=payload, verify=False)
        response.raise_for_status()
        id_payload = {"id": response.json().get("id")}
    except Exception as e:
        print("提交解密请求失败:", e)
        return {}

    # 请求获取解密结果
    try:
        response = requests.post("http://quipqiup.com/status", headers=headers, json=id_payload, verify=False)
        response.raise_for_status()
        solutions = response.json().get("solutions", [])
    except Exception as e:
        print("获取解密结果失败:", e)
        return {}

    # 组织解密结果
    result = {}
    for s in solutions:
        result[s["key"]] = s["plaintext"]
    return result


class RotCipher:
    """ROT系列加密算法实现（支持ROT3/5/10/13/18/47/ROT-5/ROT-6）"""
    @staticmethod
    def _rotate_char(char: str, base: int, shift: int, range_size: int) -> str:
        """对单个字符进行指定偏移量的 ROT 加密/解密"""
        if not char.isspace():  # 跳过空白字符
            char_code = ord(char)
            if base <= char_code < base + range_size:
                # 计算旋转后的字符代码
                char_code = (char_code - base + shift) % range_size + base
            return chr(char_code)
        return char

    @staticmethod
    def rot10(text: str, decrypt: bool = False) -> str:
        """ Avocat 执行 ROT10 加密/解密，字母旋转10位 """
        shift = -10 if decrypt else 10
        result = []
        for c in text:
            if c.isupper():
                result.append(RotCipher._rotate_char(c, 65, shift, 26))
            elif c.islower():
                result.append(RotCipher._rotate_char(c, 97, shift, 26))
            else:
                result.append(c)
        return ''.join(result)


if __name__ == '__main__':
    with open(r"attachment.txt", "r") as f:
        ct = f.read().split(' ')

    res1 = ''.join(chr(int(c, 2)) for c in ct)
    res2 = b64decode(res1[307:].encode()).decode()
    res3 = RotCipher.rot10(res2[169:])
    res4 = decrypt_with_quipqiup(res3[10][915:])
    
    for key, text in res4.items():
        if 'flag' in text:
            print(f"Key: {key}\nPlaintext: {text}\n")

            # utflag{n0w_th4ts_wh4t_i_c4ll_crypt0}

2.26 四面八方

2.26.1 题目

1
2
3
4
5
6
四方门主东方青木看着四面八方涌过来的极客，非常震惊，转头便进入了祖祠中的地下室，发现这丫传自唐朝的密室还设计了英文密码。旁边的石头上（附件中有拓本）刻着密码和密文，大家快帮助门主解出密码(答案为一串通顺语义字符串) 

key1:security
key2:information

密文啊这是，骚年加油：zhnjinhoopcfcuktlj

2.26.2 解题思路

四方密码

2.26.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
import re
from collections import OrderedDict

class FourSquareCipher:
    def __init__(self, key1, key2):
        self.matrix = 'ABCDEFGHIJKLMNOPRSTUVWXYZ'  # 不含Q的25字母表
        self.pla = 'abcdefghijklmnoprstuvwxyz'     # 明文小写字母表（不含q）
        
        # 处理密钥（移除重复字符，无需处理[]）
        self.key1 = self._process_key(key1)
        self.key2 = self._process_key(key2)
        
        # 生成加密矩阵
        self.matrix1 = self._generate_matrix(self.key1)
        self.matrix2 = self._generate_matrix(self.key2)
        
        # 明文矩阵（5x5分割）
        self.pla_list = [list(self.pla[i:i+5]) for i in range(0, 25, 5)]
        
        # 预计算位置映射表（加速查找）
        self.pla_pos = self._build_position_map(self.pla_list)
        self.matrix1_pos = self._build_position_map(self.matrix1)
        self.matrix2_pos = self._build_position_map(self.matrix2)

    def _process_key(self, key):
        """处理密钥：移除重复字符，保留大写字母，忽略其他字符"""
        # 仅保留大写字母（若输入小写则转为大写）
        key_clean = re.sub(r'[^A-Z]', '', key.upper())
        # 移除重复字符（保持首次出现顺序）
        return ''.join(OrderedDict.fromkeys(key_clean))

    def _generate_matrix(self, key):
        """生成5x5加密矩阵：密钥 + 字母表剩余字符"""
        # 过滤掉密钥中已包含的字母
        remaining_chars = [c for c in self.matrix if c not in key]
        # 拼接密钥和剩余字符，组成25字符
        full_matrix = key + ''.join(remaining_chars)
        # 按5个字符一行分割为矩阵
        return [list(full_matrix[i:i+5]) for i in range(0, 25, 5)]

    def _build_position_map(self, matrix):
        """构建字符到（行, 列）的映射字典"""
        pos_map = {}
        for row_idx, row in enumerate(matrix):
            for col_idx, char in enumerate(row):
                pos_map[char] = (row_idx, col_idx)
        return pos_map

    def encrypt(self, plaintext):
        """加密明文：处理空格和q，按对加密"""
        # 预处理：移除空格，替换q为无（或按规则替换），转为小写
        plain_clean = plaintext.replace(' ', '').replace('q', '').replace('Q', '').lower()
        # 确保长度为偶数（不足补x）
        if len(plain_clean) % 2 != 0:
            plain_clean += 'x'
        # 按两个字符一组加密
        ciphertext = []
        for i in range(0, len(plain_clean), 2):
            pair = plain_clean[i:i+2]
            ciphertext.append(self._encrypt_pair(pair))
        return ''.join(ciphertext)

    def _encrypt_pair(self, pair):
        """加密单个字符对（a, b）"""
        a, b = pair[0], pair[1]
        # 获取明文在矩阵中的位置（行, 列）
        row_a, col_a = self.pla_pos[a]
        row_b, col_b = self.pla_pos[b]
        # 四方密码规则：(row_a, col_b) 取自matrix1，(row_b, col_a) 取自matrix2
        return self.matrix1[row_a][col_b] + self.matrix2[row_b][col_a]

    def decrypt(self, ciphertext):
        """解密密文：按对解密，返回小写明文"""
        # 预处理：移除空格，保留大写字母
        cipher_clean = ciphertext.replace(' ', '').upper()
        # 按两个字符一组解密
        plaintext = []
        for i in range(0, len(cipher_clean), 2):
            pair = cipher_clean[i:i+2]
            plaintext.append(self._decrypt_pair(pair))
        return ''.join(plaintext)

    def _decrypt_pair(self, pair):
        """解密单个字符对（c1, c2）"""
        c1, c2 = pair[0], pair[1]
        # 获取密文在矩阵中的位置（行, 列）
        row_c1, col_c1 = self.matrix1_pos[c1]
        row_c2, col_c2 = self.matrix2_pos[c2]
        # 四方密码规则：(row_c1, col_c2) 和 (row_c2, col_c1) 取自明文矩阵
        return self.pla_list[row_c1][col_c2] + self.pla_list[row_c2][col_c1]


if __name__ == "__main__":
    cipher = FourSquareCipher("security", "information")
    pt = cipher.decrypt('zhnjinhoopcfcuktlj')
    print(f"flag{{{pt}}}")

    # flag{youngandsuccessful}

2.27 [NPUCTF2020]Classical Cipher

2.27.1 题目

1
2
3
4
5
6
# key.txt
解密后的flag请用flag{}包裹

压缩包密码：gsv_pvb_rh_zgyzhs

对应明文：   ***_key_**_******

2.27.2 解题思路

Atbash 密码 + 变种猪圈密码 + 古埃及象形文字

2.27.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class AtBashCipher:
    def __init__(self, key="ABCDEFGHIJKLMNOPQRSTUVWXYZ"):
        self.key = key
        # 预计算加密映射表
        self.encrypt_map = {
            key[i]: key[25 - i]
            for i in range(26)
        }
        # 解密映射表与加密相同（对称加密）
        self.decrypt_map = self.encrypt_map

    def encrypt(self, plaintext):
        """加密明文：将每个字母替换为字母表中对称位置的字母"""
        return ''.join(
            self.encrypt_map.get(c.upper(), c)
            for c in plaintext
        )

    def decrypt(self, ciphertext):
        """解密密文：与加密逻辑完全相同"""
        return self.encrypt(ciphertext)

if __name__ == '__main__':
    ct = 'gsv_pvb_rh_zgyzhs'
    result = AtBashCipher().decrypt(ct).lower()
    print(result)

    # the_key_is_atbash
    # flag{classicalcode}

2.28 [BJDCTF2020]Polybius

2.28.1 题目

1
2
3
密文：ouauuuoooeeaaiaeauieuooeeiea
hint：VGhlIGxlbmd0aCBvZiB0aGlzIHBsYWludGV4dDogMTQ=
flag:解出明文后，请加上BJD{}

2.28.2 解题思路

hint（base64）：The length of this plaintext: 14

Polybius Square Cipher（棋盘密码）：利用波利比奥斯方阵进行加密的密码方式，密文长度是明文长度的两倍，密文只有五种字符。

2.28.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
import itertools

class Polybius:
    def __init__(self, key: str):
        """
        初始化 Polybius 类
        """
        if len(key) != 5 or set(key) != set('aeoiu'):
            raise ValueError("Key 必须是 'aeoiu' 的排列")
        self.key = key

    def encrypt(self, plaintext: str) -> str:
        """
        加密函数：将明文加密为 5 元音字母构成的密文
        """
        cipher = ""
        for ch in plaintext:
            if ch == 'j':  # 传统替代 j->i
                ch = 'i'
            ascii_code = ord(ch)
            if 'a' <= ch <= 'z':
                if ascii_code > ord('i'):
                    ascii_code -= 1  # 去掉 j 后偏移
                row, col = divmod(ascii_code - 97, 5)
                cipher += self.key[row] + self.key[col]
            else:
                raise ValueError(f"不支持字符: {ch}")
        return cipher

    def decrypt(self, cipher: str) -> str:
        """
        解密函数：将密文还原为明文
        """
        if len(cipher) % 2 != 0:
            raise ValueError("密文长度必须为偶数")
        solve_c = ''.join(str(self.key.index(c)) for c in cipher)
        res = ""
        for i in range(0, len(solve_c), 2):
            row = int(solve_c[i])
            col = int(solve_c[i + 1])
            ascii_code = row * 5 + col + 97
            if ascii_code >= ord('j'):
                ascii_code += 1  # 跳过 j
            res += chr(ascii_code)
        return res


if __name__ == "__main__":
    cipher = "ouauuuoooeeaaiaeauieuooeeiea"

    for key_candidate in itertools.permutations('aeoiu'):
        key_str = ''.join(key_candidate)
        poly = Polybius(key_str)
        try:
            plaintext = poly.decrypt(cipher)
            if 'flag' in plaintext:
                print("找到可能的key:", key_str)
                print("解密结果:", plaintext)
        except Exception:
            continue

    # flag{flagispolybius}

2.29 [ACTF新生赛2020]crypto-classic1

2.29.1 题目

1
2
3
# hint.txt
哇，这里有压缩包的密码哦，于是我低下了头，看向了我的双手，试图从中找到某些规律
xdfv ujko98 edft54 xdfv pok,.; wsdr43

2.29.2 解题思路

电脑键盘密码：取每组字母环绕所包围的中心字母作为明文。根据这种规则，得到压缩包密码为：circle。

解压得到：SRLU{LZPL_S_UASHKXUPD_NXYTFTJT}，根据压缩名字提示维吉尼亚密码。

2.29.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
import string


class QwertyKeyboardPassword2:
    """围绕式电脑键盘密码"""
    def __init__(self):
        self.letter = {
            'q': 'aw21', 'w': '2qase3', 'e': '3wsdr4', 'r': '4edft5', 't': '5rfgy6', 'y': '6tghu7', 'u': '7yhji8',
            'i': '8ujko9', 'o': '9iklp0', 'p': '0ol;[-', 'a': 'qwsz', 's': 'wazxde', 'd': 'esxcfr', 'f': 'rdcvgt',
            'g': 'tfvbhy', 'h': 'ygbnju', 'j': 'uhnmki', 'k': 'ijm,lo', 'l': 'ok,.;p', 'z': 'xsa', 'x': 'zsdc', 
            'c': 'xdfv', 'v': 'cfgb', 'b': 'vghn', 'n': 'bhjm', 'm': 'njk,',

            'Q': 'AW21', 'W': '2QASE3', 'E': '3WSDR4', 'R': '4EDFT5', 'T': '5RFGY6', 'Y': '6TGHU7', 'U': '7YHJI8', 
            'I': '8UJKO9', 'O': '9IKLP0', 'P': '0OL;[-', 'A': 'QWSZ', 'S': 'WAZXDE', 'D': 'ESXCFR', 'F': 'RDCVGT', 
            'G': 'TFVBHY', 'H': 'YGBNJU', 'J': 'UHNMKI', 'K': 'IJM,LO', 'L': 'OK,.;P', 'Z': 'XSA', 'X': 'ZSDC', 
            'C': 'XDFV', 'V': 'CFGB', 'B': 'VGHN', 'N': 'BHJM', 'M': 'NJK,',

            '1': '2q`', '2': '1qw3', '3': '2we4', '4': '3er5', '5': '4rt6', '6': '5ty7', '7': '6yu8', '8': '7ui9', '9': '8io0', '0': '9op-'
        }

    def encode(self, pt):
        return ''.join(self.letter.get(i) for i in pt)

    def decode(self, ct):
        res = ''
        for i in ct:
            for key, value in self.letter.items():
                if set(i) == set(value):
                    res += key
        return res


class Vigenere:
    @staticmethod
    def decrypt(msg, key):
        """维吉尼亚解密"""
        lower_tab = string.ascii_lowercase    # 小写字母
        upper_tab = string.ascii_uppercase    # 大写字母
        digit_tab = string.digits

        plain_text = ''
        key_index = 0
        for char in msg:
            if char.isupper():
                offset = ord(key[key_index % len(key)].upper()) - ord('A')
                plain_text += upper_tab[(upper_tab.index(char) - offset) % 26]
                key_index += 1
            elif char.islower():
                offset = ord(key[key_index % len(key)].lower()) - ord('a')
                plain_text += lower_tab[(lower_tab.index(char) - offset) % 26]
                key_index += 1
            elif char.isdigit():
                offset = ord(key[key_index % len(key)].upper()) - ord('A')
                plain_text += digit_tab[(digit_tab.index(char) - offset) % 10]
                key_index += 1
            else:
                plain_text += char

        return plain_text

    @staticmethod
    def encrypt(msg, key):
        """维吉尼亚加密"""
        lower_tab = string.ascii_lowercase  # 小写字母
        upper_tab = string.ascii_uppercase  # 大写字母
        digit_tab = string.digits

        cipher_text = ''
        key_index = 0
        for char in msg:
            if char.isupper():
                offset = ord(key[key_index % len(key)].upper()) - ord('A')
                cipher_text += upper_tab[(upper_tab.index(char) + offset) % 26]
                key_index += 1
            elif char.islower():
                offset = ord(key[key_index % len(key)].lower()) - ord('a')
                cipher_text += lower_tab[(lower_tab.index(char) + offset) % 26]
                key_index += 1
            elif char.isdigit():
                offset = ord(key[key_index % len(key)].upper()) - ord('A')
                cipher_text += digit_tab[(digit_tab.index(char) + offset) % 10]
                key_index += 1
            else:
                cipher_text += char

        return cipher_text

    @staticmethod
    def recover_key_fragment(plaintext, ciphertext):
        """已知部分明文和密文，恢复维吉尼亚密钥片段"""
        key_fragment = []

        for p_char, c_char in zip(plaintext, ciphertext):
            if p_char.isalpha() and c_char.isalpha():
                p_offset = ord('A') if p_char.isupper() else ord('a')
                c_offset = ord('A') if c_char.isupper() else ord('a')

                key_val = (ord(c_char) - c_offset - (ord(p_char) - p_offset) + 26) % 26
                key_char = chr(ord('A') + key_val)  # 默认输出大写字母
                key_fragment.append(key_char)
            else:
                continue  # 非字母字符跳过

        return ''.join(key_fragment)


if __name__ == '__main__':
    ct = 'xdfv ujko98 edft54 xdfv pok,.; wsdr43'.split(' ')
    print(QwertyKeyboardPassword2().decode(ct))

    # circle

    part_pt = 'ACTF'
    part_ct = 'SRLU'
    secret_key = Vigenere.recover_key_fragment(part_pt, part_ct)
    cipher_text = r'SRLU{LZPL_S_UASHKXUPD_NXYTFTJT}'
    plain_text = Vigenere.decrypt(cipher_text, secret_key)
    print(plain_text)

    # ACTF{TKXW_A_FIDPVFFXO_VIGENERE}

2.30 浪里淘沙

2.30.1 题目

1
2
3
我有密集恐惧症，所以大家自求多福吧，把获得的单词连在一起提交即可。（我这里有一串数字：4，8，11，15，16）

tonightsuccessnoticenoticewewesuccesstonightweexamplecryptoshouldwebackspacetonightbackspaceexamplelearnwesublimlearnbackspacetheshouldwelearnfoundsublimsystemexamplesublimfoundlearnshouldmorningsublimsystemuserlearnthecryptomorningexamplenoticetonightlearntonightlearntonightsublimenterusermorningfoundtonightweenterfoundnoticethecryptomorningthebackspacelearntonightlearnsublimtonightlearnfoundenterfoundsuccesstonightsuccessuserfoundmorningtonighttheshouldsublimentertonightenterbackspacelearnexamplenoticeexamplefoundsystemsuccesssublimsuccessshouldtonightcryptowelearncryptofoundshouldsublimsublimweentertonightsuccessshouldentertheentercryptouserbackspaceshouldentersystemsuccesssystementerfoundenterlearnexampletonightnoticemorningusertonightlearnmorningtonightfoundfoundsuccessnoticesystementerlearnexamplebackspaceshouldcryptocryptosublimweexampletonighttheshouldthemorningbackspacelearntonightsystemsuccesssuccessbackspacemorningnoticeuserfoundfoundtonightmorningenterenterthefoundbackspacelearnenterentershouldthesystemfounduserlearnlearnsystemnoticetonighttheshouldlearnuserbackspaceweusernoticeshouldthewefoundsystemwecryptocryptowethebackspacesystementershouldtonightsystemnoticemorningsystemweentermorningfoundsuccessusertonightsuccesstonightbackspaceshouldweenterthewesystemusernoticesystemthelearnexamplelearnfoundlearnnoticeexamplesystemthecryptocryptolearnsystemthecryptoenterlearnexamplemorningmorningweenterentersuccessexampleuserthebackspacenoticesublimenterbackspacesuccessbackspacethesublimexamplesystemtheexamplecryptolearnuserexamplelearnsystemusersuccessenterentersuccesstheuserbackspacelearnsuccessbackspacethesublimshouldwebackspaceexamplesuccesssuccesstonightweusershouldsuccessmorningcryptomorningfoundbackspacesublimshouldentershouldnoticesuccessmorningsuccessexamplelearnshouldsublimlearntonightshoulduserbackspacesublimlearncryptosuccessenternoticetonightmorningtonightwesuccessweuserbackspaceexamplewesystemnoticemorningsystemmorningcryptolearnsystemthethefoundcryptouserlearnusersystemwemorningenterexampleshouldlearncryptofoundenterbackspacelearnenterenterbackspaceshouldbackspacetheshouldthesystemshouldshouldsuccessmorningthefoundsystementersystemtonightcryptowelearnexampleexamplesystementerbackspaceshouldtheentersublimtonightfoundfoundsuccesssuccesssystemsublimcryptoshouldentersublimmorninglearnfoundtonightcryptobackspacesuccesscryptowebackspacefoundshouldnoticeshouldmorningnoticesystemcryptosystemlearnsystemnoticemorningsystementerwemorninglearnsuccessfoundwesuccesswetheusercryptousernoticebackspacesuccessshouldtonightmorningentermorninguserenternoticefoundmorningwetonightsystemthecryptotonightcryptosystemuserthefoundexampletonightusersystemcryptosublimmorninguserthefoundbackspaceshouldsuccesscryptotonightsystemnoticebackspaceusershouldenterthecryptomorningwesublimnoticesuccessnoticeusersuccesstonightlearnweuserenterfounduserexampleshouldshouldtonightwelearnthenoticethewefoundmorningexampleshouldexamplethesuccessnoticeenterfoundthecryptonoticeuserlearnuserweenterfoundmorningsystemweexamplenoticethebackspaceexamplesublimtheusermorningtonightthesuccesscryptosuccessusersuccesstonighttonightwelearnenterenterthemorningentersystemcryptobackspacemorningsystemexamplecryptouserexamplelearnsublimsuccessusersystemfoundmorningshouldcryptotonightsublimtheexamplemorningsystemuserexampleweexamplenoticesuccesssublimnoticecryptoshouldbackspaceshouldthetonightfoundsublimbackspacebackspacetonightshouldbackspacesuccesstonightbackspacesuccessmorningsystemcryptobackspaceentertonighttonightnoticelearnshoulduserfoundexamplesystemthesuccessweusertonightcryptousernoticeenternoticebackspaceusersystemfoundusernoticeshouldlearnuserfoundexampleusermorningshouldsuccessmorningmorningexampleexamplefoundsublimfoundenterbackspacenoticelearnfoundmorningcryptonoticecryptoshouldweshouldtonightcryptobackspacesublimcryptosublimenterentersublimentercryptonoticethethesublimexampleenterentershouldlearncryptoentershouldmorninglearnnoticeuserexamplesublimtonightshouldfoundtonightsuccessshouldmorningfoundtheweuserlearnsublimsystembackspacecryptotheusertonightcryptosublimmorningmorningexamplenoticetheenterlearnshouldmorningsublimfoundtonightsublimsublimexamplefounduserexamplethefoundwemorningnoticefoundcryptosuccesssublimsublimexamplethesuccessexamplenoticesuccessbackspacesublimlearnuserexamplesuccesssuccesssystemsuccessmorningmorninglearnexamplemorningtonightfoundbackspaceenternoticemorningentersuccessmorningusermorningbackspacelearncryptoenteruserenteruserthetonighttonightsuccesslearnenterfoundsuccesssystemfoundbackspaceenterlearnsystemsublimcryptoentermorningwetonightshouldlearnenterfoundcryptonoticelearnlearnshouldfoundsuccessexampletonightthesuccessfoundusertonightenterfoundsuccessshouldmorningusernoticemorningsystemsystemsuccessshouldwelearnenterfoundexamplewethefoundweshouldsystemsystemmorningmorningbackspaceshouldentersublimentertonightsuccesssystemsystemcryptousershouldsublimfoundwetonightnoticeexamplewewesuccessfoundusertonightfoundsystemexamplecryptofoundshouldshouldsuccessenterbackspaceexampletonightthelearnnoticeuserlearnsystemsublimfoundlearnsuccesssystemshouldsublimnoticelearnsystemnoticetonightexamplefoundusernoticeenterlearnnoticecryptousersystemmorningthewesystemfoundfoundshouldsystementerenterbackspacesystemsublimcryptousermorninglearnlearntonightsublimlearnenterenterbackspacesystemuserusercryptoentershouldtheusersublimnoticeexamplemorningexamplesublimsublimbackspacesystemexampleshouldsublimlearnfoundenterbackspacelearnmorningmorningfoundthetonightmorningnoticeenterlearnusersystemtonightbackspaceexamplelearntonightbackspaceweshouldcryptosuccessbackspaceexamplesuccesstheshouldmorninguserbackspacelearnthetheshouldcryptocryptotonightbackspacecryptocryptobackspacebackspacenoticeusertonightentermorningfoundweenterexampleenterfoundusersublimsystemtheexampleexamplesystemsuccessusersublimentermorningbackspacesystemfoundlearnsystemshouldsublimsublimentershouldtheusershouldexampleexampleshouldsuccesswelearnfoundsublimshoulduserweentertonightwenoticesublimsystemlearnshouldfoundsuccessuserentersuccessmorningcryptoenteruserfoundexampletonightlearnexampleexamplefoundlearnsuccesssystembackspacecryptonoticethefoundbackspacelearncryptothelearnlearnexamplesuccessnoticenoticesystemmorningcryptotonightnoticenoticeentersuccesscryptoenterbackspacesublimexampleenterfoundtonightcryptotonightsublimnoticesuccesssublimtheentertonighttheshouldthefoundsystemtonightuserbackspacesuccessshouldwebackspacenoticebackspacebackspacenoticewecryptobackspacebackspaceusertonightlearnsuccessmorningusertonightsuccessshouldbackspacecryptoenterentershouldsublimsystemexamplemorningcryptonoticethesuccessthebackspacenoticelearnsublimlearnsuccesscryptothesuccessenternoticecryptosystemsublimsuccesswebackspaceuserenterlearnuserwewemorningsuccesslearncryptobackspacewecryptosystemlearnenterenteruserexamplefoundsystemcryptousernoticefoundusersublimbackspacewesublimnoticemorningshouldexamplenoticecryptoshouldtonightmorningthefoundsystementerentersystemthecryptobackspacesublimlearnsuccessmorningsublimsystemcryptousersublimwesuccessmorningsublimbackspacecryptobackspacesublimthelearnsuccesssublimlearncryptoweweexamplecryptowenoticelearnfoundbackspacesystemsystemexampleshouldlearnsuccesssublimcryptobackspacetonightbackspacemorningmorningnoticeshouldnoticefoundthetheshouldtheshouldfoundfoundcryptosuccessbackspacesuccessshouldweenternoticeweweshouldmorningfoundusersuccessbackspacewenoticeusersuccessenterenterexamplelearnfoundwetonightusercryptothesublimsublimtonightsuccesslearnbackspacetonightentertonightthesublimnoticewefoundcryptobackspaceenterenterlearnlearntonightexamplesystementersublimnoticecryptoshoulduseruserbackspaceuserwesublimmorningwesystemshouldtonighttheusershouldnoticefoundusernoticeentersublimwethewefoundfoundlearnfoundwecryptosystemexamplemorningcryptocryptosublimtheexamplenoticefoundlearnwelearnmorningtheenterthesystemsublimtonightsuccesssystemlearnshouldenterbackspaceentersuccesssuccessbackspaceexamplenoticeentershouldsublimlearnbackspacetheshouldexamplelearnsystemusersublimbackspacebackspacesuccesswelearntonightexamplewecryptoenterwesystemsystemsublimexamplecryptolearnmorningsublimfoundsublimfoundbackspacefoundtonighttonightnoticesuccesssuccessexampleusersuccesstonightsublimcryptosystemweenterexamplesystemthethenoticesublimtonightbackspacenoticesystemexamplethesuccesstonightmorningsuccesstonightwenoticesublimtonightwelearntonightmorningsublimbackspaceenterthetonightenterwecryptofoundtheenternoticebackspacesuccesswesystemuserexamplebackspaceentersuccesstonightsublimwemorningsuccesssuccesswesublimsuccessnoticesublimfoundlearnlearnweexamplecryptonoticelearnweusershoulduserfoundcryptolearnfoundmorningtonightmorningmorningnoticewecryptowewesuccessfoundsublimweuserentershouldshouldshouldsublimbackspacetonightenterwesublimsuccessshouldfoundthethetonightwecryptoweenterfoundcryptoshouldcryptouseruserfoundentersublimsublimthelearntheshouldnoticebackspacefoundsuccessshouldtonightentermorningsystemmorningtonightwenoticelearnbackspaceexampleusershouldnoticesublimsublimexamplethesuccessnoticesystemmorningnoticecryptosystemsublimcryptosystemsuccessshouldmorningbackspaceshouldmorninglearnnoticenoticeshouldthewewesublimsublimnoticeusersuccessentersystemfoundshouldshouldcryptobackspaceusermorningsystemshouldshouldtonightwesublimuserfoundlearnbackspacethetonightmorningexampleuserthefoundbackspaceshouldtonightcryptocryptofounduserexamplenoticecryptousernoticethenoticeshouldweshouldfoundwemorningcryptosuccesslearnfoundtonightsublimnoticenoticewefoundwewesuccesssublimsublimcryptoweexampletonightsuccessfoundshouldsuccesstonightbackspacesystemshouldwesystemnoticebackspaceusersystembackspacewenoticelearnnoticenoticesuccesslearntonightuserlearnsuccessbackspacesuccesswesystemusercryptonoticethesystemusernoticewethesuccessweshouldfoundshouldcryptomorningtonightwethewesuccesslearntheshouldweexampletonightsuccessnoticenoticemorningfoundmorningfoundusersublimsystemsuccessbackspacesuccessmorninguserthefoundweexamplemorningsublimlearnfoundfoundnoticemorningshouldweuserwemorningexamplesuccesssuccessfoundthetheshouldweusershouldtheshouldexamplenoticefoundsuccesssystemfoundshouldsublimbackspacetonightshouldsystemtonightsuccesslearntonightsystemsublimsuccesscryptobackspacesystemsublimmorningmorningshouldmorninglearnsuccesslearnmorningusermorninglearnexamplecryptoshouldbackspacesublimshouldfoundbackspacesystemsystemweexamplesystemtonightsublimmorningmorninguserfoundcryptolearnbackspaceshouldbackspacenoticesublimfoundthecryptousershouldsuccesssystemsuccessshouldsystembackspacesublimshouldsublimsystembackspaceexampleshouldbackspacesublimnoticelearnsublimuserbackspaceusersublimsuccesssublimuserusernoticeshouldsuccessnoticenoticelearnexamplesystemweexamplesublimbackspacebackspacecryptoshouldusercryptosublimbackspacesublimshouldsystemnoticenoticethesuccesssuccesslearnsystemsublimwenoticelearnusersublimsystemusernoticeuserthesuccesslearnwelearnwenoticecryptolearncryptonoticenoticebackspacecryptothecryptousercryptobackspacesuccesslearnthesystemsuccessthesystemsystemcryptosuccessbackspacesublimlearnsublimcryptobackspacelearnsublimusersublimexamplecryptosublimsystemnoticecryptocryptousertheusernoticebackspacenoticenoticethecryptocryptosystembackspacesublimbackspacecryptocryptobackspacesystemuserthenoticesystemsystemsystemusernoticethecryptouserusersystemtheusercryptoexamplenoticecryptoexamplenoticetheexampleexamplethecryptotheusernoticetheexampleexamplecryptotheexampleexamplethenoticethecryptocryptoexampletheexamplecryptocryptothenoticeexamplecryptonoticetheexampleexampleexamplecryptocryptoexampleexamplethenoticethecryptothethethethethetheexampleexamplethetheexampletheexampletheexampleexampleexampleexampleexampleexampleexampleexampleexampleexampleexampleexampleexampleexampleexampleexampleexampleexampleexample

2.30.2 解题思路

词频分析：获取每个单词出现的频率，升序排列，最后将排在 4，8，11，15，16 的单词。

2.30.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
if __name__ == "__main__":
    with open(r"浪里淘沙.txt", "r") as f:
        ct = f.read()
    lst = ['tonight','success','notice','example','should','crypto','backspace','learn','found','morning','we','system','sublim','the','user','enter']
    hint = [4, 8, 11, 15, 16]

    res = sorted([(ct.count(word), word) for word in lst if word in ct], reverse=False)
    flag = ''.join(res[i-1][1] for i in hint)
    print(f'flag{{{flag}}}')

    # flag{weshouldlearnthecrypto}

3. 现代对称密码

3.1 Rabbit

3.1.1 题目

1
U2FsdGVkX1/+ydnDPowGbjjJXhZxm2MP2AgI

3.1.2 解题思路

Rabbit 流密码：一种高速流加密算法，2003 年首次在 FSE 研讨会上提出。它使用 128 位密钥和 64 位初始化向量（IV），核心是一种能每轮输出 128 位密钥流的位流生成器，用于加密等长明文。Rabbit 设计轻量、运算高效，特别适用于资源受限设备。

3.1.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655
656
657
658
659
660
661
662
663
664
665
666
667
668
669
var CryptoJS = CryptoJS || function (n, l) {
  var i = {}
    , j = i.lib = {}
    , k = j.Base = function () {
      function b() { }
      return {
        extend: function (p) {
          b.prototype = this;
          var a = new b;
          p && a.mixIn(p);
          a.$super = this;
          return a
        },
        create: function () {
          var b = this.extend();
          b.init.apply(b, arguments);
          return b
        },
        init: function () { },
        mixIn: function (b) {
          for (var a in b)
            b.hasOwnProperty(a) && (this[a] = b[a]);
          b.hasOwnProperty("toString") && (this.toString = b.toString)
        },
        clone: function () {
          return this.$super.extend(this)
        }
      }
    }()
    , e = j.WordArray = k.extend({
      init: function (b, a) {
        b = this.words = b || [];
        this.sigBytes = a != l ? a : 4 * b.length
      },
      toString: function (b) {
        return (b || c).stringify(this)
      },
      concat: function (b) {
        var a = this.words
          , c = b.words
          , g = this.sigBytes
          , b = b.sigBytes;
        this.clamp();
        if (g % 4)
          for (var h = 0; h < b; h++)
            a[g + h >>> 2] |= (c[h >>> 2] >>> 24 - 8 * (h % 4) & 255) << 24 - 8 * ((g + h) % 4);
        else if (65535 < c.length)
          for (h = 0; h < b; h += 4)
            a[g + h >>> 2] = c[h >>> 2];
        else
          a.push.apply(a, c);
        this.sigBytes += b;
        return this
      },
      clamp: function () {
        var b = this.words
          , a = this.sigBytes;
        b[a >>> 2] &= 4294967295 << 32 - 8 * (a % 4);
        b.length = n.ceil(a / 4)
      },
      clone: function () {
        var b = k.clone.call(this);
        b.words = this.words.slice(0);
        return b
      },
      random: function (b) {
        for (var a = [], c = 0; c < b; c += 4)
          a.push(4294967296 * n.random() | 0);
        return e.create(a, b)
      }
    })
    , d = i.enc = {}
    , c = d.Hex = {
      stringify: function (b) {
        for (var a = b.words, b = b.sigBytes, c = [], g = 0; g < b; g++) {
          var h = a[g >>> 2] >>> 24 - 8 * (g % 4) & 255;
          c.push((h >>> 4).toString(16));
          c.push((h & 15).toString(16))
        }
        return c.join("")
      },
      parse: function (b) {
        for (var a = b.length, c = [], g = 0; g < a; g += 2)
          c[g >>> 3] |= parseInt(b.substr(g, 2), 16) << 24 - 4 * (g % 8);
        return e.create(c, a / 2)
      }
    }
    , a = d.Latin1 = {
      stringify: function (b) {
        for (var a = b.words, b = b.sigBytes, c = [], g = 0; g < b; g++)
                c.push(String.fromCharCode(a[g >>> 2] >>> 24 - 8 * (g % 4) & 255));
            return c.join("")
        },
        parse: function (b) {
            for (var a = b.length, c = [], g = 0; g < a; g++)
                c[g >>> 2] |= (b.charCodeAt(g) & 255) << 24 - 8 * (g % 4);
            return e.create(c, a)
        }
    }
    , f = d.Utf8 = {
        stringify: function (b) {
            try {
                return decodeURIComponent(escape(a.stringify(b)))
            } catch (c) {
                throw Error("Malformed UTF-8 data");
            }
        },
        parse: function (b) {
            return a.parse(unescape(encodeURIComponent(b)))
        }
    }
    , o = j.BufferedBlockAlgorithm = k.extend({
        reset: function () {
            this._data = e.create();
            this._nDataBytes = 0
        },
        _append: function (b) {
            "string" == typeof b && (b = f.parse(b));
            this._data.concat(b);
            this._nDataBytes += b.sigBytes
        },
        _process: function (b) {
            var a = this._data
                , c = a.words
                , g = a.sigBytes
                , h = this.blockSize
                , m = g / (4 * h)
                , m = b ? n.ceil(m) : n.max((m | 0) - this._minBufferSize, 0)
                , b = m * h
                , g = n.min(4 * b, g);
            if (b) {
                for (var o = 0; o < b; o += h)
                    this._doProcessBlock(c, o);
                o = c.splice(0, b);
                a.sigBytes -= g
            }
            return e.create(o, g)
        },
        clone: function () {
            var b = k.clone.call(this);
            b._data = this._data.clone();
            return b
        },
        _minBufferSize: 0
    });
j.Hasher = o.extend({
    init: function () {
        this.reset()
    },
    reset: function () {
        o.reset.call(this);
        this._doReset()
    },
    update: function (b) {
        this._append(b);
        this._process();
        return this
    },
    finalize: function (b) {
        b && this._append(b);
        this._doFinalize();
        return this._hash
    },
    clone: function () {
        var b = o.clone.call(this);
        b._hash = this._hash.clone();
        return b
    },
    blockSize: 16,
    _createHelper: function (b) {
        return function (a, c) {
            return b.create(c).finalize(a)
        }
    },
    _createHmacHelper: function (b) {
        return function (a, c) {
            return q.HMAC.create(b, c).finalize(a)
        }
    }
});
var q = i.algo = {};
return i
}(Math);
(function () {
var n = CryptoJS
    , l = n.lib.WordArray;
n.enc.Base64 = {
    stringify: function (i) {
        var j = i.words
            , k = i.sigBytes
            , e = this._map;
        i.clamp();
        for (var i = [], d = 0; d < k; d += 3)
            for (var c = (j[d >>> 2] >>> 24 - 8 * (d % 4) & 255) << 16 | (j[d + 1 >>> 2] >>> 24 - 8 * ((d + 1) % 4) & 255) << 8 | j[d + 2 >>> 2] >>> 24 - 8 * ((d + 2) % 4) & 255, a = 0; 4 > a && d + 0.75 * a < k; a++)
                i.push(e.charAt(c >>> 6 * (3 - a) & 63));
        if (j = e.charAt(64))
            for (; i.length % 4;)
                i.push(j);
        return i.join("")
    },
    parse: function (i) {
        var i = i.replace(/\s/g, "")
            , j = i.length
            , k = this._map
            , e = k.charAt(64);
        e && (e = i.indexOf(e),
            -1 != e && (j = e));
        for (var e = [], d = 0, c = 0; c < j; c++)
            if (c % 4) {
                var a = k.indexOf(i.charAt(c - 1)) << 2 * (c % 4)
                    , f = k.indexOf(i.charAt(c)) >>> 6 - 2 * (c % 4);
                e[d >>> 2] |= (a | f) << 24 - 8 * (d % 4);
                d++
            }
        return l.create(e, d)
    },
    _map: "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/="
}
}
)();
(function (n) {
function l(a, c, b, d, f, g, h) {
    a = a + (c & b | ~c & d) + f + h;
    return (a << g | a >>> 32 - g) + c
}
function i(a, c, b, d, f, g, h) {
    a = a + (c & d | b & ~d) + f + h;
    return (a << g | a >>> 32 - g) + c
}
function j(a, c, b, d, f, g, h) {
    a = a + (c ^ b ^ d) + f + h;
    return (a << g | a >>> 32 - g) + c
}
function k(a, c, b, d, f, g, h) {
    a = a + (b ^ (c | ~d)) + f + h;
    return (a << g | a >>> 32 - g) + c
}
var e = CryptoJS
    , d = e.lib
    , c = d.WordArray
    , d = d.Hasher
    , a = e.algo
    , f = [];
(function () {
    for (var a = 0; 64 > a; a++)
        f[a] = 4294967296 * n.abs(n.sin(a + 1)) | 0
}
)();
a = a.MD5 = d.extend({
    _doReset: function () {
        this._hash = c.create([1732584193, 4023233417, 2562383102, 271733878])
    },
    _doProcessBlock: function (a, c) {
        for (var b = 0; 16 > b; b++) {
            var d = c + b
                , e = a[d];
            a[d] = (e << 8 | e >>> 24) & 16711935 | (e << 24 | e >>> 8) & 4278255360
        }
        for (var d = this._hash.words, e = d[0], g = d[1], h = d[2], m = d[3], b = 0; 64 > b; b += 4)
            16 > b ? (e = l(e, g, h, m, a[c + b], 7, f[b]),
                m = l(m, e, g, h, a[c + b + 1], 12, f[b + 1]),
                h = l(h, m, e, g, a[c + b + 2], 17, f[b + 2]),
                g = l(g, h, m, e, a[c + b + 3], 22, f[b + 3])) : 32 > b ? (e = i(e, g, h, m, a[c + (b + 1) % 16], 5, f[b]),
                    m = i(m, e, g, h, a[c + (b + 6) % 16], 9, f[b + 1]),
                    h = i(h, m, e, g, a[c + (b + 11) % 16], 14, f[b + 2]),
                    g = i(g, h, m, e, a[c + b % 16], 20, f[b + 3])) : 48 > b ? (e = j(e, g, h, m, a[c + (3 * b + 5) % 16], 4, f[b]),
                        m = j(m, e, g, h, a[c + (3 * b + 8) % 16], 11, f[b + 1]),
                        h = j(h, m, e, g, a[c + (3 * b + 11) % 16], 16, f[b + 2]),
                        g = j(g, h, m, e, a[c + (3 * b + 14) % 16], 23, f[b + 3])) : (e = k(e, g, h, m, a[c + 3 * b % 16], 6, f[b]),
                            m = k(m, e, g, h, a[c + (3 * b + 7) % 16], 10, f[b + 1]),
                            h = k(h, m, e, g, a[c + (3 * b + 14) % 16], 15, f[b + 2]),
                            g = k(g, h, m, e, a[c + (3 * b + 5) % 16], 21, f[b + 3]));
        d[0] = d[0] + e | 0;
        d[1] = d[1] + g | 0;
        d[2] = d[2] + h | 0;
        d[3] = d[3] + m | 0
    },
    _doFinalize: function () {
        var a = this._data
            , c = a.words
            , b = 8 * this._nDataBytes
            , d = 8 * a.sigBytes;
        c[d >>> 5] |= 128 << 24 - d % 32;
        c[(d + 64 >>> 9 << 4) + 14] = (b << 8 | b >>> 24) & 16711935 | (b << 24 | b >>> 8) & 4278255360;
        a.sigBytes = 4 * (c.length + 1);
        this._process();
        a = this._hash.words;
        for (c = 0; 4 > c; c++)
            b = a[c],
                a[c] = (b << 8 | b >>> 24) & 16711935 | (b << 24 | b >>> 8) & 4278255360
    }
});
e.MD5 = d._createHelper(a);
e.HmacMD5 = d._createHmacHelper(a)
}
)(Math);
(function () {
var n = CryptoJS
    , l = n.lib
    , i = l.Base
    , j = l.WordArray
    , l = n.algo
    , k = l.EvpKDF = i.extend({
        cfg: i.extend({
            keySize: 4,
            hasher: l.MD5,
            iterations: 1
        }),
        init: function (e) {
            this.cfg = this.cfg.extend(e)
        },
        compute: function (e, d) {
            for (var c = this.cfg, a = c.hasher.create(), f = j.create(), i = f.words, k = c.keySize, c = c.iterations; i.length < k;) {
                b && a.update(b);
                var b = a.update(e).finalize(d);
                a.reset();
                for (var l = 1; l < c; l++)
                    b = a.finalize(b),
                        a.reset();
                f.concat(b)
            }
            f.sigBytes = 4 * k;
            return f
        }
    });
n.EvpKDF = function (e, d, c) {
    return k.create(c).compute(e, d)
}
}
)();
CryptoJS.lib.Cipher || function (n) {
var l = CryptoJS
    , i = l.lib
    , j = i.Base
    , k = i.WordArray
    , e = i.BufferedBlockAlgorithm
    , d = l.enc.Base64
    , c = l.algo.EvpKDF
    , a = i.Cipher = e.extend({
        cfg: j.extend(),
        createEncryptor: function (a, b) {
            return this.create(this._ENC_XFORM_MODE, a, b)
        },
        createDecryptor: function (a, b) {
            return this.create(this._DEC_XFORM_MODE, a, b)
        },
        init: function (a, b, c) {
            this.cfg = this.cfg.extend(c);
            this._xformMode = a;
            this._key = b;
            this.reset()
        },
        reset: function () {
            e.reset.call(this);
            this._doReset()
        },
        process: function (a) {
            this._append(a);
            return this._process()
        },
        finalize: function (a) {
            a && this._append(a);
            return this._doFinalize()
        },
        keySize: 4,
        ivSize: 4,
        _ENC_XFORM_MODE: 1,
        _DEC_XFORM_MODE: 2,
        _createHelper: function () {
            return function (a) {
                return {
                    encrypt: function (b, c, d) {
                        return ("string" == typeof c ? r : p).encrypt(a, b, c, d)
                    },
                    decrypt: function (b, c, d) {
                        return ("string" == typeof c ? r : p).decrypt(a, b, c, d)
                    }
                }
            }
        }()
    });
i.StreamCipher = a.extend({
    _doFinalize: function () {
        return this._process(!0)
    },
    blockSize: 1
});
var f = l.mode = {}
    , o = i.BlockCipherMode = j.extend({
        createEncryptor: function (a, b) {
            return this.Encryptor.create(a, b)
        },
        createDecryptor: function (a, b) {
            return this.Decryptor.create(a, b)
        },
        init: function (a, b) {
            this._cipher = a;
            this._iv = b
        }
    })
    , f = f.CBC = function () {
        function a(b, c, g) {
            var d = this._iv;
            d ? this._iv = n : d = this._prevBlock;
            for (var h = 0; h < g; h++)
                b[c + h] ^= d[h]
        }
        var b = o.extend();
        b.Encryptor = b.extend({
            processBlock: function (b, c) {
                var d = this._cipher
                    , h = d.blockSize;
                a.call(this, b, c, h);
                d.encryptBlock(b, c);
                this._prevBlock = b.slice(c, c + h)
            }
        });
        b.Decryptor = b.extend({
            processBlock: function (b, c) {
                var d = this._cipher
                    , h = d.blockSize
                    , f = b.slice(c, c + h);
                d.decryptBlock(b, c);
                a.call(this, b, c, h);
                this._prevBlock = f
            }
        });
        return b
    }()
    , q = (l.pad = {}).Pkcs7 = {
        pad: function (a, b) {
            for (var c = 4 * b, c = c - a.sigBytes % c, d = c << 24 | c << 16 | c << 8 | c, f = [], e = 0; e < c; e += 4)
                f.push(d);
            c = k.create(f, c);
            a.concat(c)
        },
        unpad: function (a) {
            a.sigBytes -= a.words[a.sigBytes - 1 >>> 2] & 255
        }
    };
i.BlockCipher = a.extend({
    cfg: a.cfg.extend({
        mode: f,
        padding: q
    }),
    reset: function () {
        a.reset.call(this);
        var b = this.cfg
            , c = b.iv
            , b = b.mode;
        if (this._xformMode == this._ENC_XFORM_MODE)
            var d = b.createEncryptor;
        else
            d = b.createDecryptor,
                this._minBufferSize = 1;
        this._mode = d.call(b, this, c && c.words)
    },
    _doProcessBlock: function (a, b) {
        this._mode.processBlock(a, b)
    },
    _doFinalize: function () {
        var a = this.cfg.padding;
        if (this._xformMode == this._ENC_XFORM_MODE) {
            a.pad(this._data, this.blockSize);
            var b = this._process(!0)
        } else
            b = this._process(!0),
                a.unpad(b);
        return b
    },
    blockSize: 4
});
var b = i.CipherParams = j.extend({
    init: function (a) {
        this.mixIn(a)
    },
    toString: function (a) {
        return (a || this.formatter).stringify(this)
    }
})
    , f = (l.format = {}).OpenSSL = {
        stringify: function (a) {
            var b = a.ciphertext
                , a = a.salt
                , b = (a ? k.create([1398893684, 1701076831]).concat(a).concat(b) : b).toString(d);
            return b = b.replace(/(.{64})/g, "$1\n")
        },
        parse: function (a) {
            var a = d.parse(a)
                , c = a.words;
            if (1398893684 == c[0] && 1701076831 == c[1]) {
                var f = k.create(c.slice(2, 4));
                c.splice(0, 4);
                a.sigBytes -= 16
            }
            return b.create({
                ciphertext: a,
                salt: f
            })
        }
    }
    , p = i.SerializableCipher = j.extend({
        cfg: j.extend({
            format: f
        }),
        encrypt: function (a, c, d, f) {
            var f = this.cfg.extend(f)
                , e = a.createEncryptor(d, f)
                , c = e.finalize(c)
                , e = e.cfg;
            return b.create({
                ciphertext: c,
                key: d,
                iv: e.iv,
                algorithm: a,
                mode: e.mode,
                padding: e.padding,
                blockSize: a.blockSize,
                formatter: f.format
            })
        },
        decrypt: function (a, b, c, d) {
            d = this.cfg.extend(d);
            b = this._parse(b, d.format);
            return a.createDecryptor(c, d).finalize(b.ciphertext)
        },
        _parse: function (a, b) {
            return "string" == typeof a ? b.parse(a) : a
        }
    })
    , l = (l.kdf = {}).OpenSSL = {
        compute: function (a, d, f, e) {
            e || (e = k.random(8));
            a = c.create({
                keySize: d + f
            }).compute(a, e);
            f = k.create(a.words.slice(d), 4 * f);
            a.sigBytes = 4 * d;
            return b.create({
                key: a,
                iv: f,
                salt: e
            })
        }
    }
    , r = i.PasswordBasedCipher = p.extend({
        cfg: p.cfg.extend({
            kdf: l
        }),
        encrypt: function (a, b, c, d) {
            d = this.cfg.extend(d);
            c = d.kdf.compute(c, a.keySize, a.ivSize);
            d.iv = c.iv;
            a = p.encrypt.call(this, a, b, c.key, d);
            a.mixIn(c);
            return a
        },
        decrypt: function (a, b, c, d) {
            d = this.cfg.extend(d);
            b = this._parse(b, d.format);
            c = d.kdf.compute(c, a.keySize, a.ivSize, b.salt);
            d.iv = c.iv;
            return p.decrypt.call(this, a, b, c.key, d)
        }
    })
}();
(function () {
function n() {
    var d = this._X
        , c = this._C;
    c[0] = c[0] + 1295307597 + this._b | 0;
    c[1] = c[1] + 3545052371 + (1295307597 > c[0] >>> 0 ? 1 : 0) | 0;
    c[2] = c[2] + 886263092 + (3545052371 > c[1] >>> 0 ? 1 : 0) | 0;
    c[3] = c[3] + 1295307597 + (886263092 > c[2] >>> 0 ? 1 : 0) | 0;
    c[4] = c[4] + 3545052371 + (1295307597 > c[3] >>> 0 ? 1 : 0) | 0;
    c[5] = c[5] + 886263092 + (3545052371 > c[4] >>> 0 ? 1 : 0) | 0;
    c[6] = c[6] + 1295307597 + (886263092 > c[5] >>> 0 ? 1 : 0) | 0;
    c[7] = c[7] + 3545052371 + (1295307597 > c[6] >>> 0 ? 1 : 0) | 0;
    this._b = 3545052371 > c[7] >>> 0 ? 1 : 0;
    for (var a = 0; 8 > a; a++) {
        var f = d[a] + c[a]
            , e = f & 65535
            , i = f >>> 16;
        k[a] = ((e * e >>> 17) + e * i >>> 15) + i * i ^ ((f & 4294901760) * f | 0) + ((f & 65535) * f | 0)
    }
    var c = k[0]
        , a = k[1]
        , f = k[2]
        , e = k[3]
        , i = k[4]
        , b = k[5]
        , j = k[6]
        , l = k[7];
    d[0] = c + (l << 16 | l >>> 16) + (j << 16 | j >>> 16) | 0;
    d[1] = a + (c << 8 | c >>> 24) + l | 0;
    d[2] = f + (a << 16 | a >>> 16) + (c << 16 | c >>> 16) | 0;
    d[3] = e + (f << 8 | f >>> 24) + a | 0;
    d[4] = i + (e << 16 | e >>> 16) + (f << 16 | f >>> 16) | 0;
    d[5] = b + (i << 8 | i >>> 24) + e | 0;
    d[6] = j + (b << 16 | b >>> 16) + (i << 16 | i >>> 16) | 0;
    d[7] = l + (j << 8 | j >>> 24) + b | 0
}
var l = CryptoJS
    , i = l.lib.StreamCipher
    , j = []
    , k = []
    , e = l.algo.Rabbit = i.extend({
        _doReset: function () {
            for (var d = this._key.words, c = d[0], a = d[1], f = d[2], e = d[3], d = this._X = [c, e << 16 | f >>> 16, a, c << 16 | e >>> 16, f, a << 16 | c >>> 16, e, f << 16 | a >>> 16], c = this._C = [f << 16 | f >>> 16, c & 4294901760 | a & 65535, e << 16 | e >>> 16, a & 4294901760 | f & 65535, c << 16 | c >>> 16, f & 4294901760 | e & 65535, a << 16 | a >>> 16, e & 4294901760 | c & 65535], a = this._b = 0; 4 > a; a++)
                n.call(this);
            for (a = 0; 8 > a; a++)
                c[a] ^= d[a + 4 & 7];
            if (d = this.cfg.iv) {
                a = d.words;
                d = a[0];
                a = a[1];
                d = (d << 8 | d >>> 24) & 16711935 | (d << 24 | d >>> 8) & 4278255360;
                a = (a << 8 | a >>> 24) & 16711935 | (a << 24 | a >>> 8) & 4278255360;
                f = d >>> 16 | a & 4294901760;
                e = a << 16 | d & 65535;
                c[0] ^= d;
                c[1] ^= f;
                c[2] ^= a;
                c[3] ^= e;
                c[4] ^= d;
                c[5] ^= f;
                c[6] ^= a;
                c[7] ^= e;
                for (a = 0; 4 > a; a++)
                    n.call(this)
            }
        },
        _doProcessBlock: function (d, c) {
            var a = this._X;
            n.call(this);
            j[0] = a[0] ^ a[5] >>> 16 ^ a[3] << 16;
            j[1] = a[2] ^ a[7] >>> 16 ^ a[5] << 16;
            j[2] = a[4] ^ a[1] >>> 16 ^ a[7] << 16;
            j[3] = a[6] ^ a[3] >>> 16 ^ a[1] << 16;
            for (a = 0; 4 > a; a++) {
                var e = j[a]
                    , e = (e << 8 | e >>> 24) & 16711935 | (e << 24 | e >>> 8) & 4278255360;
                d[c + a] ^= e
            }
        },
        blockSize: 4,
        ivSize: 2
    });
l.Rabbit = i._createHelper(e)
}
)();


function main() {
    const ciphertext = "U2FsdGVkX1/+ydnDPowGbjjJXhZxm2MP2AgI";

    // 解密
    const bytes = CryptoJS.Rabbit.decrypt(ciphertext, '', {
    iv: '',
    mode: CryptoJS.mode.CBC,
    padding: CryptoJS.pad.Pkcs7
    });
    
    console.log("flag{" + CryptoJS.enc.Utf8.stringify(bytes) + "}");
}

main();

// flag{Cute_Rabbit}

3.2 [ACTF新生赛2020]crypto-aes

3.2.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from Cryptodome.Cipher import AES
import os
import gmpy2
from flag import FLAG
from Cryptodome.Util.number import *

def main():
    key=os.urandom(2)*16
    iv=os.urandom(16)
    print(bytes_to_long(key)^bytes_to_long(iv))
    aes=AES.new(key,AES.MODE_CBC,iv)
    enc_flag = aes.encrypt(FLAG)
    print(enc_flag)
if __name__=="__main__":
    main()

91144196586662942563895769614300232343026691029427747065707381728622849079757
b'\x8c-\xcd\xde\xa7\xe9\x7f.b\x8aKs\xf1\xba\xc75\xc4d\x13\x07\xac\xa4&\xd6\x91\xfe\xf3\x14\x10|\xf8p'

3.2.2 解题思路

参数设置不当、高位泄露

AES 32 字节密钥与 16 字节 IV 进行异或，高 16 字节泄露。且密钥只有 2 字节的熵，后面是重复 16 次。可以求出 key 和 iv。

3.2.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from Crypto.Cipher import AES
from Crypto.Util.number import bytes_to_long, long_to_bytes

def aes_decrypt(ct, key, iv):
    aes = AES.new(key, AES.MODE_CBC, iv)
    flag = aes.decrypt(ct)
    return flag

if __name__ == '__main__':
    leak = 91144196586662942563895769614300232343026691029427747065707381728622849079757
    ciphertext = b'\x8c-\xcd\xde\xa7\xe9\x7f.b\x8aKs\xf1\xba\xc75\xc4d\x13\x07\xac\xa4&\xd6\x91\xfe\xf3\x14\x10|\xf8p'

    key = long_to_bytes(leak)[:16]*2
    iv = long_to_bytes(leak ^ bytes_to_long(key))
    print(aes_decrypt(ciphertext, key, iv))

    # b'actf{W0W_y0u_can_so1v3_AES_now!}'

4. 现代非对称密码

4.1 RSA

4.1.1 题目

1
2
在一次 RSA 密钥对生成中，假设 p=473398607161，q=4511491，e=17
求解出 d 作为 flag 提交

4.1.2 解题思路

标准 RSA 解密

$ \begin{gathered}
\phi(N)=(p-1)*(q-1) \
d=e^{-1} \mod \phi(N)
\end{gathered} $

4.1.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from Crypto.Util.number import inverse

def p_q_e_d(p, q, e):
    phi = (p-1)*(q-1)
    d = inverse(e, phi)
    return d


if __name__ == '__main__':
    p = 473398607161
    q = 4511491
    e = 17
    print(f'flag{{{p_q_e_d(p, q, e)}}}')
    
    # flag{125631357777427553}

4.2 rsarsa

4.2.1 题目

1
2
3
4
5
6
7
8
9
Math is cool! Use the RSA algorithm to decode the secret message, c, p, q, and e are parameters for the RSA algorithm.


p =  9648423029010515676590551740010426534945737639235739800643989352039852507298491399561035009163427050370107570733633350911691280297777160200625281665378483
q =  11874843837980297032092405848653656852760910154543380907650040190704283358909208578251063047732443992230647903887510065547947313543299303261986053486569407
e =  65537
c =  83208298995174604174773590298203639360540024871256126892889661345742403314929861939100492666605647316646576486526217457006376842280869728581726746401583705899941768214138742259689334840735633553053887641847651173776251820293087212885670180367406807406765923638973161375817392737747832762751690104423869019034

Use RSA to find the secret message

4.2.2 解题思路

标准 RSA 解密

4.2.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
from math import prod
from sympy import totient
from base64 import b64decode
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
from Crypto.Util.number import inverse, long_to_bytes


def standard_rsa_decryption(e, c, primes=None, n=None, phi=None, ct_format='int'):
    """
    标准 RSA 解密
    """
    if not phi:
        if n:
            phi = totient(n)
        else:
            phi = prod(p - 1 for p in primes)
            n = prod(p for p in primes)

    d = inverse(e, phi)
    
    if ct_format == 'base64':
        p, q = primes[0], primes[1]
        key_info = RSA.construct((n, e, d, p, q))
        key = RSA.importKey(key_info.exportKey())
        key = PKCS1_OAEP.new(key)
        m = key.decrypt(b64decode(c)).decode()
    else:
        m = pow(c, d, n)

    return m


if __name__ == '__main__':
    p = 9648423029010515676590551740010426534945737639235739800643989352039852507298491399561035009163427050370107570733633350911691280297777160200625281665378483
    q = 11874843837980297032092405848653656852760910154543380907650040190704283358909208578251063047732443992230647903887510065547947313543299303261986053486569407
    e = 65537
    c = 83208298995174604174773590298203639360540024871256126892889661345742403314929861939100492666605647316646576486526217457006376842280869728581726746401583705899941768214138742259689334840735633553053887641847651173776251820293087212885670180367406807406765923638973161375817392737747832762751690104423869019034

    m = standard_rsa_decryption(e, c, [p, q])
    print(f'flag{{{m}}}')

    # flag{5577446633554466577768879988}

4.3 RSA1

4.3.1 题目

1
2
3
4
5
p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229 
q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469 
dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929 
dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041 
c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852

4.3.2 解题思路

$ dp、dq $ 泄露

已知 $ p、q、dp、dq、c $ 求明文 $ m $

4.3.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from Crypto.Util.number import long_to_bytes, GCD, inverse


def p_q_dp_dq_c(p, q, dp, dq, c):
    """
    已知 p, q, dp, dq, c 求 d 和明文 m
    """
    n = p*q
    _gcd = GCD(p - 1, q - 1)
    d = ((dp - dq) // _gcd) * inverse((q - 1) // _gcd, (p - 1) // _gcd) * (q - 1) + dq

    return pow(c, d, n)


if __name__ == "__main__":
    p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229 
    q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469 
    dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929 
    dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041 
    c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852

    plaintext = p_q_dp_dq_c(p, q, dp, dq, c)
    print(long_to_bytes(plaintext))

    # b'noxCTF{W31c0m3_70_Ch1n470wn}'

4.4 RSA3

4.4.1 题目

1
2
3
4
5
c1=22322035275663237041646893770451933509324701913484303338076210603542612758956262869640822486470121149424485571361007421293675516338822195280313794991136048140918842471219840263536338886250492682739436410013436651161720725855484866690084788721349555662019879081501113222996123305533009325964377798892703161521852805956811219563883312896330156298621674684353919547558127920925706842808914762199011054955816534977675267395009575347820387073483928425066536361482774892370969520740304287456555508933372782327506569010772537497541764311429052216291198932092617792645253901478910801592878203564861118912045464959832566051361
n=22708078815885011462462049064339185898712439277226831073457888403129378547350292420267016551819052430779004755846649044001024141485283286483130702616057274698473611149508798869706347501931583117632710700787228016480127677393649929530416598686027354216422565934459015161927613607902831542857977859612596282353679327773303727004407262197231586324599181983572622404590354084541788062262164510140605868122410388090174420147752408554129789760902300898046273909007852818474030770699647647363015102118956737673941354217692696044969695308506436573142565573487583507037356944848039864382339216266670673567488871508925311154801
e1=11187289
c2=18702010045187015556548691642394982835669262147230212731309938675226458555210425972429418449273410535387985931036711854265623905066805665751803269106880746769003478900791099590239513925449748814075904017471585572848473556490565450062664706449128415834787961947266259789785962922238701134079720414228414066193071495304612341052987455615930023536823801499269773357186087452747500840640419365011554421183037505653461286732740983702740822671148045619497667184586123657285604061875653909567822328914065337797733444640351518775487649819978262363617265797982843179630888729407238496650987720428708217115257989007867331698397
e2=9647291

4.4.2 解题思路

RSA 的共模攻击

$ m 、n $ 相同；$ e 、 c $ 不同，且 $ e_1 $ 和 $ e_2 $ 互质。

4.4.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from gmpy2 import gcdext
from Crypto.Util.number import long_to_bytes

def common_modulus_attack(e1, e2, c1, c2, n):
    _, r, s = gmpy2.gcdext(e1, e2)
    m = pow(c1, r, n) * pow(c2, s, n) % n
    return m

if __name__ == '__main__': 
    e1 = 11187289
    e2 = 9647291
    n = 22708078815885011462462049064339185898712439277226831073457888403129378547350292420267016551819052430779004755846649044001024141485283286483130702616057274698473611149508798869706347501931583117632710700787228016480127677393649929530416598686027354216422565934459015161927613607902831542857977859612596282353679327773303727004407262197231586324599181983572622404590354084541788062262164510140605868122410388090174420147752408554129789760902300898046273909007852818474030770699647647363015102118956737673941354217692696044969695308506436573142565573487583507037356944848039864382339216266670673567488871508925311154801
    c1=22322035275663237041646893770451933509324701913484303338076210603542612758956262869640822486470121149424485571361007421293675516338822195280313794991136048140918842471219840263536338886250492682739436410013436651161720725855484866690084788721349555662019879081501113222996123305533009325964377798892703161521852805956811219563883312896330156298621674684353919547558127920925706842808914762199011054955816534977675267395009575347820387073483928425066536361482774892370969520740304287456555508933372782327506569010772537497541764311429052216291198932092617792645253901478910801592878203564861118912045464959832566051361
    c2=18702010045187015556548691642394982835669262147230212731309938675226458555210425972429418449273410535387985931036711854265623905066805665751803269106880746769003478900791099590239513925449748814075904017471585572848473556490565450062664706449128415834787961947266259789785962922238701134079720414228414066193071495304612341052987455615930023536823801499269773357186087452747500840640419365011554421183037505653461286732740983702740822671148045619497667184586123657285604061875653909567822328914065337797733444640351518775487649819978262363617265797982843179630888729407238496650987720428708217115257989007867331698397 

    m = common_modulus_attack(e1, e2, c1, c2, n)
    print(long_to_bytes(m))

    # b'flag{49d91077a1abcb14f1a9d546c80be9ef}'

4.5 RSA2

4.5.1 题目

1
2
3
4
e = 65537
n = 248254007851526241177721526698901802985832766176221609612258877371620580060433101538328030305219918697643619814200930679612109885533801335348445023751670478437073055544724280684733298051599167660303645183146161497485358633681492129668802402065797789905550489547645118787266601929429724133167768465309665906113
dp = 905074498052346904643025132879518330691925174573054004621877253318682675055421970943552016695528560364834446303196939207056642927148093290374440210503657
c = 140423670976252696807533673586209400575664282100684119784203527124521188996403826597436883766041879067494280957410201958935737360380801845453829293997433414188838725751796261702622028587211560353362847191060306578510511380965162133472698713063592621028959167072781482562673683090590521214218071160287665180751

4.5.2 解题思路

$ dp、dq $ 泄露

已知 $ dp\ (dq)、n、e、c $，求明文 $ m $

4.5.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
from Crypto.Util.number import inverse, long_to_bytes


def dp_n_e_c(dp: int, e: int, n: int, c: int) -> bytes:
    """
    已知 dp (dq)、n、e、c，求明文 m
    """
    # 遍历可能的k值，寻找有效的p
    for k in range(1, e):
        if (dp * e - 1) % k: continue
        p = ((dp * e - 1) // k) + 1
        if n % p: continue
        q = n // p
        d = inverse(e, (p - 1) * (q - 1))
        return pow(c, d, n)


if __name__ == '__main__':
    e = 65537
    n = 248254007851526241177721526698901802985832766176221609612258877371620580060433101538328030305219918697643619814200930679612109885533801335348445023751670478437073055544724280684733298051599167660303645183146161497485358633681492129668802402065797789905550489547645118787266601929429724133167768465309665906113
    dp = 905074498052346904643025132879518330691925174573054004621877253318682675055421970943552016695528560364834446303196939207056642927148093290374440210503657
    c = 140423670976252696807533673586209400575664282100684119784203527124521188996403826597436883766041879067494280957410201958935737360380801845453829293997433414188838725751796261702622028587211560353362847191060306578510511380965162133472698713063592621028959167072781482562673683090590521214218071160287665180751

    plaintext = dp_n_e_c(dp, e, n, c)
    print(long_to_bytes(plaintext))

    # b'flag{wow_leaking_dp_breaks_rsa?_98924743502}'

4.6 RSA

4.6.1 题目

1
2
3
4
5
6
7
8
9
# flag.enc
41 96 C0 59 4A 5E 00 0A 96 B8 78 B6 7C D7 24 79
5B 13 A8 F2 CA 54 DA 06 D0 F1 9C 28 BE 68 9B 62

# pub.key
-----BEGIN PUBLIC KEY-----
MDwwDQYJKoZIhvcNAQEBBQADKwAwKAIhAMAzLFxkrkcYL2wch21CM2kQVFpY9+7+
/AvKr1rzQczdAgMBAAE=
-----END PUBLIC KEY-----

4.6.2 解题思路

提取公钥 + 大素数分解 + 标准 RSA 解密

4.6.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
import rsa
import requests
from math import prod
from sympy import totient
from base64 import b64decode
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
from Crypto.Util.number import inverse, long_to_bytes


class ExtractKey:
    @staticmethod
    def extract_public_key(pem_str):
        """
        提取 PEM 格式公钥中的 n（模数）和 e（公钥指数）
        """
        pubkey = rsa.PublicKey.load_pkcs1_openssl_pem(pem_str.encode())
        return pubkey.n, pubkey.e

    @staticmethod
    def extract_private_key(pem_str):
        """
        提取 PEM 格式私钥中的 n（模数）和 d（私钥指数）
        """
        privkey = rsa.PrivateKey.load_pkcs1(pem_str.encode())
        return privkey.n, privkey.d
    

def queryFactors(n):
    """查询整数 n 的质因数分解结果"""
    response = requests.get(f"http://factordb.com/api?query={n}")
    return [int(factor) for factor, count in response.json()["factors"] for _ in range(int(count))]


def standard_rsa_decryption(e, c, primes=None, n=None, phi=None, ct_format='int'):
    """
    标准 RSA 解密
    """
    if not phi:
        if n:
            phi = totient(n)
        else:
            phi = prod(p - 1 for p in primes)
            n = prod(p for p in primes)

    d = inverse(e, phi)
    
    if ct_format == 'base64':
        p, q = primes[0], primes[1]
        key_info = RSA.construct((n, e, d, p, q))
        key = RSA.importKey(key_info.exportKey())
        key = PKCS1_OAEP.new(key)
        m = key.decrypt(b64decode(c)).decode()
    else:
        m = pow(c, d, n)

    return m


if __name__ == "__main__":
    public_pem = """
    -----BEGIN PUBLIC KEY-----
    MDwwDQYJKoZIhvcNAQEBBQADKwAwKAIhAMAzLFxkrkcYL2wch21CM2kQVFpY9+7+
    /AvKr1rzQczdAgMBAAE=
    -----END PUBLIC KEY-----
    """

    n, e = ExtractKey.extract_public_key(public_pem)
    p, q = queryFactors(n)

    with open(r"flag.enc", "rb") as f:
        c = int.from_bytes(f.read(), 'big')
        m = standard_rsa_decryption(p, q, e, c)
        print(long_to_bytes(m))

        # flag{decrypt_256}

4.7 RSAROLL

4.7.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
# 题目.txt
RSA roll！roll！roll！
Only number and a-z
（don't use editor which MS provide）

# data.txt
{920139713,19}

704796792
752211152
274704164
18414022
368270835
483295235
263072905
459788476
483295235
459788476
663551792
475206804
459788476
428313374
475206804
459788476
425392137
704796792
458265677
341524652
483295235
534149509
425392137
428313374
425392137
341524652
458265677
263072905
483295235
828509797
341524652
425392137
475206804
428313374
483295235
475206804
459788476
306220148

4.7.2 解题思路

前两个是 $ (n,e) $，后面是密文分块，按行依次解密。

4.7.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import re
from Crypto.Util.number import inverse

def p_q_e_d(p, q, e):
    phi = (p-1)*(q-1)
    d = inverse(e, phi)
    return d

if __name__ == "__main__":
    n = 920139713
    p = 49891
    q = 18443
    e = 19
    d = p_q_e_d(p, q, e)
    
    m = ""
    with open("roll.txt",'r') as f:
        for line in f:
            line = line.strip()
            if re.match(r'^\d+$', line):
                md = str(pow(int(line), d, n))
                m += chr(int(md))
    print(m)
    
    # flag{13212je2ue28fy71w8u87y31r78eu1e2}

4.8 Dangerous RSA

4.8.1 题目

1
2
3
4
5
6
7
littlE littlE RSA Big Big Dangerous

# problem
#n:  0x52d483c27cd806550fbe0e37a61af2e7cf5e0efb723dfc81174c918a27627779b21fa3c851e9e94188eaee3d5cd6f752406a43fbecb53e80836ff1e185d3ccd7782ea846c2e91a7b0808986666e0bdadbfb7bdd65670a589a4d2478e9adcafe97c6ee23614bcb2ecc23580f4d2e3cc1ecfec25c50da4bc754dde6c8bfd8d1fc16956c74d8e9196046a01dc9f3024e11461c294f29d7421140732fedacac97b8fe50999117d27943c953f18c4ff4f8c258d839764078d4b6ef6e8591e0ff5563b31a39e6374d0d41c8c46921c25e5904a817ef8e39e5c9b71225a83269693e0b7e3218fc5e5a1e8412ba16e588b3d6ac536dce39fcdfce81eec79979ea6872793L
#e:  0x3
#c:0x10652cdfaa6b63f6d7bd1109da08181e500e5643f5b240a9024bfa84d5f2cac9310562978347bb232d63e7289283871efab83d84ff5a7b64a94a79d34cfbd4ef121723ba1f663e514f83f6f01492b4e13e1bb4296d96ea5a353d3bf2edd2f449c03c4a3e995237985a596908adc741f32365
so,how to get the message?

4.8.2 解题思路

RSA 低公钥指数攻击

特点：$ e $ 很小，$ m $ 很小，$ n $ 很大

如果明文很小，$ e $ 次方后仍小于模数 $ n（m^e \lt n ）$，则直接对密文开 $ e $ 次方即可得到明文。

如果明文 $ e $ 次方结果比 $ n $ 大（$ m^e \gt n $），则有 $ C=m^e+k \cdot n $，尝试爆破 $ k $，如果找到一个 $ k $ 能开 $ e $ 次方根，则找到明文。

4.8.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import itertools
from gmpy2 import iroot
from Crypto.Util.number import long_to_bytes, GCD, inverse


def low_public_exponent_attack(n, c, e=None, lower=None, upper=None, phi=None):
    """
    RSA 低公钥指数攻击
    """
    if e is not None:
        # 小 e 且 m^e < n，可直接开 e 次方根
        for k in itertools.count():
            candidate = c + k * n
            root, exact = iroot(candidate, e)
            if exact:
                return int(root)
    elif phi is not None and lower is not None and upper is not None:
        # 若未知 e，则爆破 e，满足 gcd(e, φ) = 1 并计算 d
        for e_candidate in range(lower, upper):
            if GCD(e_candidate, phi) == 1:
                d = inverse(e_candidate, phi)
                m = pow(c, d, n)
                if b'flag' in long_to_bytes(m):
                    return m
    else:
        raise ValueError("参数不完整：请提供 e，或 (phi + low + high)")


if __name__ == "__main__":
    n = 0x52d483c27cd806550fbe0e37a61af2e7cf5e0efb723dfc81174c918a27627779b21fa3c851e9e94188eaee3d5cd6f752406a43fbecb53e80836ff1e185d3ccd7782ea846c2e91a7b0808986666e0bdadbfb7bdd65670a589a4d2478e9adcafe97c6ee23614bcb2ecc23580f4d2e3cc1ecfec25c50da4bc754dde6c8bfd8d1fc16956c74d8e9196046a01dc9f3024e11461c294f29d7421140732fedacac97b8fe50999117d27943c953f18c4ff4f8c258d839764078d4b6ef6e8591e0ff5563b31a39e6374d0d41c8c46921c25e5904a817ef8e39e5c9b71225a83269693e0b7e3218fc5e5a1e8412ba16e588b3d6ac536dce39fcdfce81eec79979ea6872793
    e = 0x3
    c = 0x10652cdfaa6b63f6d7bd1109da08181e500e5643f5b240a9024bfa84d5f2cac9310562978347bb232d63e7289283871efab83d84ff5a7b64a94a79d34cfbd4ef121723ba1f663e514f83f6f01492b4e13e1bb4296d96ea5a353d3bf2edd2f449c03c4a3e995237985a596908adc741f32365
    m = low_public_exponent_attack(n, c, e)
    print(long_to_bytes(m))

    # b'flag{25df8caf006ee5db94d48144c33b2c3b}'

4.9 [HDCTF2019]basic rsa

4.9.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import gmpy2
from Crypto.Util.number import *
from binascii import a2b_hex,b2a_hex

flag = "*****************"

p = 262248800182277040650192055439906580479
q = 262854994239322828547925595487519915551

e = 65533
n = p*q


c = pow(int(b2a_hex(flag),16),e,n)

print c

# 27565231154623519221597938803435789010285480123476977081867877272451638645710

4.9.2 解题思路

标准 RSA 解密

4.9.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
from math import prod
from sympy import totient
from base64 import b64decode
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
from Crypto.Util.number import inverse, long_to_bytes


def standard_rsa_decryption(e, c, primes=None, n=None, phi=None, ct_format='int'):
    """
    标准 RSA 解密
    """
    if not phi:
        if n:
            phi = totient(n)
        else:
            phi = prod(p - 1 for p in primes)
            n = prod(p for p in primes)

    d = inverse(e, phi)
    
    if ct_format == 'base64':
        p, q = primes[0], primes[1]
        key_info = RSA.construct((n, e, d, p, q))
        key = RSA.importKey(key_info.exportKey())
        key = PKCS1_OAEP.new(key)
        m = key.decrypt(b64decode(c)).decode()
    else:
        m = pow(c, d, n)

    return m


if __name__ == "__main__":
    p = 262248800182277040650192055439906580479
    q = 262854994239322828547925595487519915551
    e = 65533
    c = 27565231154623519221597938803435789010285480123476977081867877272451638645710

    m = standard_rsa_decryption(e, c, [p, q])
    print(long_to_bytes(m))

    # b'flag{B4by_Rs4}'

4.10 [GUET-CTF2019]BabyRSA

4.10.1 题目

1
2
3
4
5
p+q : 0x1232fecb92adead91613e7d9ae5e36fe6bb765317d6ed38ad890b4073539a6231a6620584cea5730b5af83a3e80cf30141282c97be4400e33307573af6b25e2ea
(p+1)(q+1) : 0x5248becef1d925d45705a7302700d6a0ffe5877fddf9451a9c1181c4d82365806085fd86fbaab08b6fc66a967b2566d743c626547203b34ea3fdb1bc06dd3bb765fd8b919e3bd2cb15bc175c9498f9d9a0e216c2dde64d81255fa4c05a1ee619fc1fc505285a239e7bc655ec6605d9693078b800ee80931a7a0c84f33c851740
e : 0xe6b1bee47bd63f615c7d0a43c529d219
d : 0x2dde7fbaed477f6d62838d55b0d0964868cf6efb2c282a5f13e6008ce7317a24cb57aec49ef0d738919f47cdcd9677cd52ac2293ec5938aa198f962678b5cd0da344453f521a69b2ac03647cdd8339f4e38cec452d54e60698833d67f9315c02ddaa4c79ebaa902c605d7bda32ce970541b2d9a17d62b52df813b2fb0c5ab1a5
enc_flag : 0x50ae00623211ba6089ddfae21e204ab616f6c9d294e913550af3d66e85d0c0693ed53ed55c46d8cca1d7c2ad44839030df26b70f22a8567171a759b76fe5f07b3c5a6ec89117ed0a36c0950956b9cde880c575737f779143f921d745ac3bb0e379c05d9a3cc6bf0bea8aa91e4d5e752c7eb46b2e023edbc07d24a7c460a34a9a

4.10.2 解题思路

已知 $ p+q $ 和 $ (p+1) \cdot (q+1) $ 可求 $ n $，标准 RSA 解密

4.10.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from Crypto.Util.number import long_to_bytes


if __name__ == "__main__":
    d = 0x2dde7fbaed477f6d62838d55b0d0964868cf6efb2c282a5f13e6008ce7317a24cb57aec49ef0d738919f47cdcd9677cd52ac2293ec5938aa198f962678b5cd0da344453f521a69b2ac03647cdd8339f4e38cec452d54e60698833d67f9315c02ddaa4c79ebaa902c605d7bda32ce970541b2d9a17d62b52df813b2fb0c5ab1a5
    e = 0xe6b1bee47bd63f615c7d0a43c529d219
    c = 0x50ae00623211ba6089ddfae21e204ab616f6c9d294e913550af3d66e85d0c0693ed53ed55c46d8cca1d7c2ad44839030df26b70f22a8567171a759b76fe5f07b3c5a6ec89117ed0a36c0950956b9cde880c575737f779143f921d745ac3bb0e379c05d9a3cc6bf0bea8aa91e4d5e752c7eb46b2e023edbc07d24a7c460a34a9a
    
    # n = p*q = (p+1)(q+1) - (p+q) - 1
    Add = 0x1232fecb92adead91613e7d9ae5e36fe6bb765317d6ed38ad890b4073539a6231a6620584cea5730b5af83a3e80cf30141282c97be4400e33307573af6b25e2ea
    Mul = 0x5248becef1d925d45705a7302700d6a0ffe5877fddf9451a9c1181c4d82365806085fd86fbaab08b6fc66a967b2566d743c626547203b34ea3fdb1bc06dd3bb765fd8b919e3bd2cb15bc175c9498f9d9a0e216c2dde64d81255fa4c05a1ee619fc1fc505285a239e7bc655ec6605d9693078b800ee80931a7a0c84f33c851740
    n = Mul - Add - 1
    
    m = pow(c, d, n)
    print(long_to_bytes(m))

    # b'flag{cc7490e-78ab-11e9-b422-8ba97e5da1fd}'

4.11 rsa2

4.11.1 题目

1
2
3
4
5
N = 101991809777553253470276751399264740131157682329252673501792154507006158434432009141995367241962525705950046253400188884658262496534706438791515071885860897552736656899566915731297225817250639873643376310103992170646906557242832893914902053581087502512787303322747780420210884852166586717636559058152544979471
e = 46731919563265721307105180410302518676676135509737992912625092976849075262192092549323082367518264378630543338219025744820916471913696072050291990620486581719410354385121760761374229374847695148230596005409978383369740305816082770283909611956355972181848077519920922059268376958811713365106925235218265173085

import hashlib
flag = "flag{" + hashlib.md5(hex(d)).hexdigest() + "}"

4.11.2 解题思路

大素数分解 $ n $，已知 $ n、e $ 求 $ d $

4.11.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import hashlib
import requests
from Crypto.Util.number import inverse

def queryFactors(n):
    """查询整数n的质因数分解结果"""
    response = requests.get(f"http://factordb.com/api?query={n}")
    return [int(factor) for factor, count in response.json()["factors"] for _ in range(int(count))]


if __name__ == '__main__':
    N = 101991809777553253470276751399264740131157682329252673501792154507006158434432009141995367241962525705950046253400188884658262496534706438791515071885860897552736656899566915731297225817250639873643376310103992170646906557242832893914902053581087502512787303322747780420210884852166586717636559058152544979471
    e = 46731919563265721307105180410302518676676135509737992912625092976849075262192092549323082367518264378630543338219025744820916471913696072050291990620486581719410354385121760761374229374847695148230596005409978383369740305816082770283909611956355972181848077519920922059268376958811713365106925235218265173085
    p, q = queryFactors(N)
    d = inverse(e, (p-1)*(q-1))
    print(hex(d))
    print(f"flag{{{hashlib.md5(b'0x13b8f87d588e2aa4a27296cf2898f56ab4c8deb5a1222ec080e23afecaf7f975L').hexdigest()}}}")
    
    # flag{47bf28da384590448e0b0d23909a25a4}

4.12 RSA5

4.12.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
m = xxxxxxxx
e = 65537
========== n c ==========
n = 20474918894051778533305262345601880928088284471121823754049725354072477155873778848055073843345820697886641086842612486541250183965966001591342031562953561793332341641334302847996108417466360688139866505179689516589305636902137210185624650854906780037204412206309949199080005576922775773722438863762117750429327585792093447423980002401200613302943834212820909269713876683465817369158585822294675056978970612202885426436071950214538262921077409076160417436699836138801162621314845608796870206834704116707763169847387223307828908570944984416973019427529790029089766264949078038669523465243837675263858062854739083634207
c = 974463908243330865728978769213595400782053398596897741316275722596415018912929508637393850919224969271766388710025195039896961956062895570062146947736340342927974992616678893372744261954172873490878805483241196345881721164078651156067119957816422768524442025688079462656755605982104174001635345874022133045402344010045961111720151990412034477755851802769069309069018738541854130183692204758761427121279982002993939745343695671900015296790637464880337375511536424796890996526681200633086841036320395847725935744757993013352804650575068136129295591306569213300156333650910795946800820067494143364885842896291126137320

n = 20918819960648891349438263046954902210959146407860980742165930253781318759285692492511475263234242002509419079545644051755251311392635763412553499744506421566074721268822337321637265942226790343839856182100575539845358877493718334237585821263388181126545189723429262149630651289446553402190531135520836104217160268349688525168375213462570213612845898989694324269410202496871688649978370284661017399056903931840656757330859626183773396574056413017367606446540199973155630466239453637232936904063706551160650295031273385619470740593510267285957905801566362502262757750629162937373721291789527659531499435235261620309759
c = 15819636201971185538694880505120469332582151856714070824521803121848292387556864177196229718923770810072104155432038682511434979353089791861087415144087855679134383396897817458726543883093567600325204596156649305930352575274039425470836355002691145864435755333821133969266951545158052745938252574301327696822347115053614052423028835532509220641378760800693351542633860702225772638930501021571415907348128269681224178300248272689705308911282208685459668200507057183420662959113956077584781737983254788703048275698921427029884282557468334399677849962342196140864403989162117738206246183665814938783122909930082802031855

n = 25033254625906757272369609119214202033162128625171246436639570615263949157363273213121556825878737923265290579551873824374870957467163989542063489416636713654642486717219231225074115269684119428086352535471683359486248203644461465935500517901513233739152882943010177276545128308412934555830087776128355125932914846459470221102007666912211992310538890654396487111705385730502843589727289829692152177134753098649781412247065660637826282055169991824099110916576856188876975621376606634258927784025787142263367152947108720757222446686415627479703666031871635656314282727051189190889008763055811680040315277078928068816491
c = 4185308529416874005831230781014092407198451385955677399668501833902623478395669279404883990725184332709152443372583701076198786635291739356770857286702107156730020004358955622511061410661058982622055199736820808203841446796305284394651714430918690389486920560834672316158146453183789412140939029029324756035358081754426645160033262924330248675216108270980157049705488620263485129480952814764002865280019185127662449318324279383277766416258142275143923532168798413011028271543085249029048997452212503111742302302065401051458066585395360468447460658672952851643547193822775218387853623453638025492389122204507555908862

n = 21206968097314131007183427944486801953583151151443627943113736996776787181111063957960698092696800555044199156765677935373149598221184792286812213294617749834607696302116136745662816658117055427803315230042700695125718401646810484873064775005221089174056824724922160855810527236751389605017579545235876864998419873065217294820244730785120525126565815560229001887622837549118168081685183371092395128598125004730268910276024806808565802081366898904032509920453785997056150497645234925528883879419642189109649009132381586673390027614766605038951015853086721168018787523459264932165046816881682774229243688581614306480751
c = 4521038011044758441891128468467233088493885750850588985708519911154778090597136126150289041893454126674468141393472662337350361712212694867311622970440707727941113263832357173141775855227973742571088974593476302084111770625764222838366277559560887042948859892138551472680654517814916609279748365580610712259856677740518477086531592233107175470068291903607505799432931989663707477017904611426213770238397005743730386080031955694158466558475599751940245039167629126576784024482348452868313417471542956778285567779435940267140679906686531862467627238401003459101637191297209422470388121802536569761414457618258343550613

n = 22822039733049388110936778173014765663663303811791283234361230649775805923902173438553927805407463106104699773994158375704033093471761387799852168337898526980521753614307899669015931387819927421875316304591521901592823814417756447695701045846773508629371397013053684553042185725059996791532391626429712416994990889693732805181947970071429309599614973772736556299404246424791660679253884940021728846906344198854779191951739719342908761330661910477119933428550774242910420952496929605686154799487839923424336353747442153571678064520763149793294360787821751703543288696726923909670396821551053048035619499706391118145067
c = 15406498580761780108625891878008526815145372096234083936681442225155097299264808624358826686906535594853622687379268969468433072388149786607395396424104318820879443743112358706546753935215756078345959375299650718555759698887852318017597503074317356745122514481807843745626429797861463012940172797612589031686718185390345389295851075279278516147076602270178540690147808314172798987497259330037810328523464851895621851859027823681655934104713689539848047163088666896473665500158179046196538210778897730209572708430067658411755959866033531700460551556380993982706171848970460224304996455600503982223448904878212849412357

n = 21574139855341432908474064784318462018475296809327285532337706940126942575349507668289214078026102682252713757703081553093108823214063791518482289846780197329821139507974763780260290309600884920811959842925540583967085670848765317877441480914852329276375776405689784571404635852204097622600656222714808541872252335877037561388406257181715278766652824786376262249274960467193961956690974853679795249158751078422296580367506219719738762159965958877806187461070689071290948181949561254144310776943334859775121650186245846031720507944987838489723127897223416802436021278671237227993686791944711422345000479751187704426369
c = 20366856150710305124583065375297661819795242238376485264951185336996083744604593418983336285185491197426018595031444652123288461491879021096028203694136683203441692987069563513026001861435722117985559909692670907347563594578265880806540396777223906955491026286843168637367593400342814725694366078337030937104035993569672959361347287894143027186846856772983058328919716702982222142848848117768499996617588305301483085428547267337070998767412540225911508196842253134355901263861121500650240296746702967594224401650220168780537141654489215019142122284308116284129004257364769474080721001708734051264841350424152506027932

n = 25360227412666612490102161131174584819240931803196448481224305250583841439581008528535930814167338381983764991296575637231916547647970573758269411168219302370541684789125112505021148506809643081950237623703181025696585998044695691322012183660424636496897073045557400768745943787342548267386564625462143150176113656264450210023925571945961405709276631990731602198104287528528055650050486159837612279600415259486306154947514005408907590083747758953115486124865486720633820559135063440942528031402951958557630833503775112010715604278114325528993771081233535247118481765852273252404963430792898948219539473312462979849137
c = 19892772524651452341027595619482734356243435671592398172680379981502759695784087900669089919987705675899945658648623800090272599154590123082189645021800958076861518397325439521139995652026377132368232502108620033400051346127757698623886142621793423225749240286511666556091787851683978017506983310073524398287279737680091787333547538239920607761080988243639547570818363788673249582783015475682109984715293163137324439862838574460108793714172603672477766831356411304446881998674779501188163600664488032943639694828698984739492200699684462748922883550002652913518229322945040819064133350314536378694523704793396169065179

n = 22726855244632356029159691753451822163331519237547639938779517751496498713174588935566576167329576494790219360727877166074136496129927296296996970048082870488804456564986667129388136556137013346228118981936899510687589585286517151323048293150257036847475424044378109168179412287889340596394755257704938006162677656581509375471102546261355748251869048003600520034656264521931808651038524134185732929570384705918563982065684145766427962502261522481994191989820110575981906998431553107525542001187655703534683231777988419268338249547641335718393312295800044734534761692799403469497954062897856299031257454735945867491191
c = 6040119795175856407541082360023532204614723858688636724822712717572759793960246341800308149739809871234313049629732934797569781053000686185666374833978403290525072598774001731350244744590772795701065129561898116576499984185920661271123665356132719193665474235596884239108030605882777868856122378222681140570519180321286976947154042272622411303981011302586225630859892731724640574658125478287115198406253847367979883768000812605395482952698689604477719478947595442185921480652637868335673233200662100621025061500895729605305665864693122952557361871523165300206070325660353095592778037767395360329231331322823610060006

n = 23297333791443053297363000786835336095252290818461950054542658327484507406594632785712767459958917943095522594228205423428207345128899745800927319147257669773812669542782839237744305180098276578841929496345963997512244219376701787616046235397139381894837435562662591060768476997333538748065294033141610502252325292801816812268934171361934399951548627267791401089703937389012586581080223313060159456238857080740699528666411303029934807011214953984169785844714159627792016926490955282697877141614638806397689306795328344778478692084754216753425842557818899467945102646776342655167655384224860504086083147841252232760941
c = 5418120301208378713115889465579964257871814114515046096090960159737859076829258516920361577853903925954198406843757303687557848302302200229295916902430205737843601806700738234756698575708612424928480440868739120075888681672062206529156566421276611107802917418993625029690627196813830326369874249777619239603300605876865967515719079797115910578653562787899019310139945904958024882417833736304894765433489476234575356755275147256577387022873348906900149634940747104513850154118106991137072643308620284663108283052245750945228995387803432128842152251549292698947407663643895853432650029352092018372834457054271102816934

n = 28873667904715682722987234293493200306976947898711255064125115933666968678742598858722431426218914462903521596341771131695619382266194233561677824357379805303885993804266436810606263022097900266975250431575654686915049693091467864820512767070713267708993899899011156106766178906700336111712803362113039613548672937053397875663144794018087017731949087794894903737682383916173267421403408140967713071026001874733487295007501068871044649170615709891451856792232315526696220161842742664778581287321318748202431466508948902745314372299799561625186955234673012098210919745879882268512656931714326782335211089576897310591491
c = 9919880463786836684987957979091527477471444996392375244075527841865509160181666543016317634963512437510324198702416322841377489417029572388474450075801462996825244657530286107428186354172836716502817609070590929769261932324275353289939302536440310628698349244872064005700644520223727670950787924296004296883032978941200883362653993351638545860207179022472492671256630427228461852668118035317021428675954874947015197745916918197725121122236369382741533983023462255913924692806249387449016629865823316402366017657844166919846683497851842388058283856219900535567427103603869955066193425501385255322097901531402103883869

n = 22324685947539653722499932469409607533065419157347813961958075689047690465266404384199483683908594787312445528159635527833904475801890381455653807265501217328757871352731293000303438205315816792663917579066674842307743845261771032363928568844669895768092515658328756229245837025261744260614860746997931503548788509983868038349720225305730985576293675269073709022350700836510054067641753713212999954307022524495885583361707378513742162566339010134354907863733205921845038918224463903789841881400814074587261720283879760122070901466517118265422863420376921536734845502100251460872499122236686832189549698020737176683019
c = 1491527050203294989882829248560395184804977277747126143103957219164624187528441047837351263580440686474767380464005540264627910126483129930668344095814547592115061057843470131498075060420395111008619027199037019925701236660166563068245683975787762804359520164701691690916482591026138582705558246869496162759780878437137960823000043988227303003876410503121370163303711603359430764539337597866862508451528158285103251810058741879687875218384160282506172706613359477657215420734816049393339593755489218588796607060261897905233453268671411610631047340459487937479511933450369462213795738933019001471803157607791738538467

n = 27646746423759020111007828653264027999257847645666129907789026054594393648800236117046769112762641778865620892443423100189619327585811384883515424918752749559627553637785037359639801125213256163008431942593727931931898199727552768626775618479833029101249692573716030706695702510982283555740851047022672485743432464647772882314215176114732257497240284164016914018689044557218920300262234652840632406067273375269301008409860193180822366735877288205783314326102263756503786736122321348320031950012144905869556204017430593656052867939493633163499580242224763404338807022510136217187779084917996171602737036564991036724299
c = 21991524128957260536043771284854920393105808126700128222125856775506885721971193109361315961129190814674647136464887087893990660894961612838205086401018885457667488911898654270235561980111174603323721280911197488286585269356849579263043456316319476495888696219344219866516861187654180509247881251251278919346267129904739277386289240394384575124331135655943513831009934023397457082184699737734388823763306805326430395849935770213817533387235486307008892410920611669932693018165569417445885810825749609388627231235840912644654685819620931663346297596334834498661789016450371769203650109994771872404185770230172934013971

n = 20545487405816928731738988374475012686827933709789784391855706835136270270933401203019329136937650878386117187776530639342572123237188053978622697282521473917978282830432161153221216194169879669541998840691383025487220850872075436064308499924958517979727954402965612196081404341651517326364041519250125036424822634354268773895465698920883439222996581226358595873993976604699830613932320720554130011671297944433515047180565484495191003887599891289037982010216357831078328159028953222056918189365840711588671093333013117454034313622855082795813122338562446223041211192277089225078324682108033843023903550172891959673551
c = 14227439188191029461250476692790539654619199888487319429114414557975376308688908028140817157205579804059783807641305577385724758530138514972962209062230576107406142402603484375626077345190883094097636019771377866339531511965136650567412363889183159616188449263752475328663245311059988337996047359263288837436305588848044572937759424466586870280512424336807064729894515840552404756879590698797046333336445465120445087587621743906624279621779634772378802959109714400516183718323267273824736540168545946444437586299214110424738159957388350785999348535171553569373088251552712391288365295267665691357719616011613628772175

n = 27359727711584277234897157724055852794019216845229798938655814269460046384353568138598567755392559653460949444557879120040796798142218939251844762461270251672399546774067275348291003962551964648742053215424620256999345448398805278592777049668281558312871773979931343097806878701114056030041506690476954254006592555275342579529625231194321357904668512121539514880704046969974898412095675082585315458267591016734924646294357666924293908418345508902112711075232047998775303603175363964055048589769318562104883659754974955561725694779754279606726358588862479198815999276839234952142017210593887371950645418417355912567987
c = 3788529784248255027081674540877016372807848222776887920453488878247137930578296797437647922494510483767651150492933356093288965943741570268943861987024276610712717409139946409513963043114463933146088430004237747163422802959250296602570649363016151581364006795894226599584708072582696996740518887606785460775851029814280359385763091078902301957226484620428513604630585131511167015763190591225884202772840456563643159507805711004113901417503751181050823638207803533111429510911616160851391754754434764819568054850823810901159821297849790005646102129354035735350124476838786661542089045509656910348676742844957008857457

n = 27545937603751737248785220891735796468973329738076209144079921449967292572349424539010502287564030116831261268197384650511043068738911429169730640135947800885987171539267214611907687570587001933829208655100828045651391618089603288456570334500533178695238407684702251252671579371018651675054368606282524673369983034682330578308769886456335818733827237294570476853673552685361689144261552895758266522393004116017849397346259119221063821663280935820440671825601452417487330105280889520007917979115568067161590058277418371493228631232457972494285014767469893647892888681433965857496916110704944758070268626897045014782837
c = 14069112970608895732417039977542732665796601893762401500878786871680645798754783315693511261740059725171342404186571066972546332813667711135661176659424619936101038903439144294886379322591635766682645179888058617577572409307484708171144488708410543462972008179994594087473935638026612679389759756811490524127195628741262871304427908481214992471182859308828778119005750928935764927967212343526503410515793717201360360437981322576798056276657140363332700714732224848346808963992302409037706094588964170239521193589470070839790404597252990818583717869140229811712295005710540476356743378906642267045723633874011649259842

n = 25746162075697911560263181791216433062574178572424600336856278176112733054431463253903433128232709054141607100891177804285813783247735063753406524678030561284491481221681954564804141454666928657549670266775659862814924386584148785453647316864935942772919140563506305666207816897601862713092809234429096584753263707828899780979223118181009293655563146526792388913462557306433664296966331469906428665127438829399703002867800269947855869262036714256550075520193125987011945192273531732276641728008406855871598678936585324782438668746810516660152018244253008092470066555687277138937298747951929576231036251316270602513451
c = 17344284860275489477491525819922855326792275128719709401292545608122859829827462088390044612234967551682879954301458425842831995513832410355328065562098763660326163262033200347338773439095709944202252494552172589503915965931524326523663289777583152664722241920800537867331030623906674081852296232306336271542832728410803631170229642717524942332390842467035143631504401140727083270732464237443915263865880580308776111219718961746378842924644142127243573824972533819479079381023103585862099063382129757560124074676150622288706094110075567706403442920696472627797607697962873026112240527498308535903232663939028587036724

n = 23288486934117120315036919418588136227028485494137930196323715336208849327833965693894670567217971727921243839129969128783853015760155446770590696037582684845937132790047363216362087277861336964760890214059732779383020349204803205725870225429985939570141508220041286857810048164696707018663758416807708910671477407366098883430811861933014973409390179948577712579749352299440310543689035651465399867908428885541237776143404376333442949397063249223702355051571790555151203866821867908531733788784978667478707672984539512431549558672467752712004519300318999208102076732501412589104904734983789895358753664077486894529499
c = 10738254418114076548071448844964046468141621740603214384986354189105236977071001429271560636428075970459890958274941762528116445171161040040833357876134689749846940052619392750394683504816081193432350669452446113285638982551762586656329109007214019944975816434827768882704630460001209452239162896576191876324662333153835533956600295255158377025198426950944040643235430211011063586032467724329735785947372051759042138171054165854842472990583800899984893232549092766400510300083585513014171220423103452292891496141806956300396540682381668367564569427813092064053993103537635994311143010708814851867239706492577203899024

n = 19591441383958529435598729113936346657001352578357909347657257239777540424811749817783061233235817916560689138344041497732749011519736303038986277394036718790971374656832741054547056417771501234494768509780369075443550907847298246275717420562375114406055733620258777905222169702036494045086017381084272496162770259955811174440490126514747876661317750649488774992348005044389081101686016446219264069971370646319546429782904810063020324704138495608761532563310699753322444871060383693044481932265801505819646998535192083036872551683405766123968487907648980900712118052346174533513978009131757167547595857552370586353973
c = 3834917098887202931981968704659119341624432294759361919553937551053499607440333234018189141970246302299385742548278589896033282894981200353270637127213483172182529890495903425649116755901631101665876301799865612717750360089085179142750664603454193642053016384714515855868368723508922271767190285521137785688075622832924829248362774476456232826885801046969384519549385428259591566716890844604696258783639390854153039329480726205147199247183621535172450825979047132495439603840806501254997167051142427157381799890725323765558803808030109468048682252028720241357478614704610089120810367192414352034177484688502364022887

n = 19254242571588430171308191757871261075358521158624745702744057556054652332495961196795369630484782930292003238730267396462491733557715379956969694238267908985251699834707734400775311452868924330866502429576951934279223234676654749272932769107390976321208605516299532560054081301829440688796904635446986081691156842271268059970762004259219036753174909942343204432795076377432107630203621754552804124408792358220071862369443201584155711893388877350138023238624566616551246804054720492816226651467017802504094070614892556444425915920269485861799532473383304622064493223627552558344088839860178294589481899206318863310603
c = 6790553533991297205804561991225493105312398825187682250780197510784765226429663284220400480563039341938599783346724051076211265663468643826430109013245014035811178295081939958687087477312867720289964506097819762095244479129359998867671811819738196687884696680463458661374310994610760009474264115750204920875527434486437536623589684519411519100170291423367424938566820315486507444202022408003879118465761273916755290898112991525546114191064022991329724370064632569903856189236177894007766690782630247443895358893983735822824243487181851098787271270256780891094405121947631088729917398317652320497765101790132679171889

n = 26809700251171279102974962949184411136459372267620535198421449833298448092580497485301953796619185339316064387798092220298630428207556482805739803420279056191194360049651767412572609187680508073074653291350998253938793269214230457117194434853888765303403385824786231859450351212449404870776320297419712486574804794325602760347306432927281716160368830187944940128907971027838510079519466846176106565164730963988892400240063089397720414921398936399927948235195085202171264728816184532651138221862240969655185596628285814057082448321749567943946273776184657698104465062749244327092588237927996419620170254423837876806659
c = 386213556608434013769864727123879412041991271528990528548507451210692618986652870424632219424601677524265011043146748309774067894985069288067952546139416819404039688454756044862784630882833496090822568580572859029800646671301748901528132153712913301179254879877441322285914544974519727307311002330350534857867516466612474769753577858660075830592891403551867246057397839688329172530177187042229028685862036140779065771061933528137423019407311473581832405899089709251747002788032002094495379614686544672969073249309703482556386024622814731015767810042969813752548617464974915714425595351940266077021672409858645427346


4.12.2 解题思路

模不互素：存在两个或更多模数 $ n $ 且其中至少一对 $ n_i $ 和 $ n_j $ 不互质。

4.12.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
import re
from math import prod
from sympy import totient
from base64 import b64decode
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
from Crypto.Util.number import inverse, long_to_bytes, GCD


def standard_rsa_decryption(e, c, primes=None, n=None, phi=None, ct_format='int'):
    """
    标准 RSA 解密
    """
    if not phi:
        if n:
            phi = totient(n)
        else:
            phi = prod(p - 1 for p in primes)
            n = prod(p for p in primes)

    d = inverse(e, phi)
    
    if ct_format == 'base64':
        p, q = primes[0], primes[1]
        key_info = RSA.construct((n, e, d, p, q))
        key = RSA.importKey(key_info.exportKey())
        key = PKCS1_OAEP.new(key)
        m = key.decrypt(b64decode(c)).decode()
    else:
        m = pow(c, d, n)

    return m


def non_coprime_moduli(n_list):
    """
    模不互素
    """
    result = []
    
    n = len(n_list)
    for i in range(n):
        for j in range(i + 1, n):  # j 从 i+1 开始，避免重复检查
            current_gcd = GCD(n_list[i], n_list[j])
            if current_gcd != 1:
                result.append((n_list[i], n_list[j], current_gcd))

    if result:
        print("找到不互质的模数对：")
        for i, j, gcd_val in result:
            print(f"模数 {i} 和模数 {j}, GCD = {gcd_val}")
    else:
        print("所有模数对均互质")

    return result


if __name__ == '__main__':
    with open('1.txt', 'r') as f:
        content = f.read()
    
    # 使用正则表达式匹配所有 n=xxx 和 c=xxx 对
    pattern = r'n\s*=\s*(\S+)\s*c\s*=\s*(\S+)'
    pairs = re.findall(pattern, content, re.DOTALL)
    
    e = 65537
    cn_list = {int(n): int(c) for n, c in pairs}
    pairs = non_coprime_moduli(list(cn_list.keys()))
    
    p, n = pairs[0][2], pairs[0][0]
    q = n // p
    c = cn_list[n]
    m = standard_rsa_decryption(e, cn_list[n], [p, q])
    print(long_to_bytes(m))

    # b'flag{abdcbe5fd94e23b3de429223ab9c2fdf}'

4.13 [NCTF2019]childRSA

4.13.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from random import choice
from Crypto.Util.number import isPrime, sieve_base as primes
from flag import flag


def getPrime(bits):
    while True:
        n = 2
        while n.bit_length() < bits:
            n *= choice(primes)
        if isPrime(n + 1):
            return n + 1

e = 0x10001
m = int.from_bytes(flag.encode(), 'big')
p, q = [getPrime(2048) for _ in range(2)]
n = p * q
c = pow(m, e, n)

# n = 32849718197337581823002243717057659218502519004386996660885100592872201948834155543125924395614928962750579667346279456710633774501407292473006312537723894221717638059058796679686953564471994009285384798450493756900459225040360430847240975678450171551048783818642467506711424027848778367427338647282428667393241157151675410661015044633282064056800913282016363415202171926089293431012379261585078566301060173689328363696699811123592090204578098276704877408688525618732848817623879899628629300385790344366046641825507767709276622692835393219811283244303899850483748651722336996164724553364097066493953127153066970594638491950199605713033004684970381605908909693802373826516622872100822213645899846325022476318425889580091613323747640467299866189070780620292627043349618839126919699862580579994887507733838561768581933029077488033326056066378869170169389819542928899483936705521710423905128732013121538495096959944889076705471928490092476616709838980562233255542325528398956185421193665359897664110835645928646616337700617883946369110702443135980068553511927115723157704586595844927607636003501038871748639417378062348085980873502535098755568810971926925447913858894180171498580131088992227637341857123607600275137768132347158657063692388249513
# c = 26308018356739853895382240109968894175166731283702927002165268998773708335216338997058314157717147131083296551313334042509806229853341488461087009955203854253313827608275460592785607739091992591431080342664081962030557042784864074533380701014585315663218783130162376176094773010478159362434331787279303302718098735574605469803801873109982473258207444342330633191849040553550708886593340770753064322410889048135425025715982196600650740987076486540674090923181664281515197679745907830107684777248532278645343716263686014941081417914622724906314960249945105011301731247324601620886782967217339340393853616450077105125391982689986178342417223392217085276465471102737594719932347242482670320801063191869471318313514407997326350065187904154229557706351355052446027159972546737213451422978211055778164578782156428466626894026103053360431281644645515155471301826844754338802352846095293421718249819728205538534652212984831283642472071669494851823123552827380737798609829706225744376667082534026874483482483127491533474306552210039386256062116345785870668331513725792053302188276682550672663353937781055621860101624242216671635824311412793495965628876036344731733142759495348248970313655381407241457118743532311394697763283681852908564387282605279108

4.13.2 解题思路

Smooth 光滑攻击：Pollard’s p−1 攻击

已知 $ a $ 与 $ p $ 互质，且 $ p $ 为素数，根据费马小定理有：

$$
a^{p-1} \equiv 1 \pmod{p}
$$
设 $ p - 1 = m_1 \cdot m_2 \cdot m_3 \cdots m_n $，且 $ \max(m_1, m_2, m_3, \ldots, m_n) \le B $，则有：

$$
p - 1 \mid B!
$$
进一步推出：

$$
a^{B!} \equiv 1 \pmod{p}
$$

即：

$$
a^{B!} - 1 = k p
$$

又因为 $ N = p \cdot q $，所以：

$$
\gcd(a^{B!} - 1,\ N) = p
$$

4.13.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
from math import prod
from sympy import totient
from base64 import b64decode
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
from Crypto.Util.number import inverse, GCD, long_to_bytes, sieve_base as primes


def standard_rsa_decryption(e, c, primes=None, n=None, phi=None, ct_format='int'):
    """
    标准 RSA 解密
    """
    if not phi:
        if n:
            phi = totient(n)
        else:
            phi = prod(p - 1 for p in primes)
            n = prod(p for p in primes)

    d = inverse(e, phi)
    
    if ct_format == 'base64':
        p, q = primes[0], primes[1]
        key_info = RSA.construct((n, e, d, p, q))
        key = RSA.importKey(key_info.exportKey())
        key = PKCS1_OAEP.new(key)
        m = key.decrypt(b64decode(c)).decode()
    else:
        m = pow(c, d, n)

    return m



def Pollards_p_1(N, B=2):
    '''
    Pollard's p−1 攻击
    '''
    a = 2
    while(True):
        a = pow(a, B, N)        # 递推计算 a^B!
        p = GCD(a - 1, N)       # 尝试计算 p
        if p != 1 and p != B:
            return p
        B += 1

if __name__ == '__main__':
    e = 65537
    n = 32849718197337581823002243717057659218502519004386996660885100592872201948834155543125924395614928962750579667346279456710633774501407292473006312537723894221717638059058796679686953564471994009285384798450493756900459225040360430847240975678450171551048783818642467506711424027848778367427338647282428667393241157151675410661015044633282064056800913282016363415202171926089293431012379261585078566301060173689328363696699811123592090204578098276704877408688525618732848817623879899628629300385790344366046641825507767709276622692835393219811283244303899850483748651722336996164724553364097066493953127153066970594638491950199605713033004684970381605908909693802373826516622872100822213645899846325022476318425889580091613323747640467299866189070780620292627043349618839126919699862580579994887507733838561768581933029077488033326056066378869170169389819542928899483936705521710423905128732013121538495096959944889076705471928490092476616709838980562233255542325528398956185421193665359897664110835645928646616337700617883946369110702443135980068553511927115723157704586595844927607636003501038871748639417378062348085980873502535098755568810971926925447913858894180171498580131088992227637341857123607600275137768132347158657063692388249513
    c = 26308018356739853895382240109968894175166731283702927002165268998773708335216338997058314157717147131083296551313334042509806229853341488461087009955203854253313827608275460592785607739091992591431080342664081962030557042784864074533380701014585315663218783130162376176094773010478159362434331787279303302718098735574605469803801873109982473258207444342330633191849040553550708886593340770753064322410889048135425025715982196600650740987076486540674090923181664281515197679745907830107684777248532278645343716263686014941081417914622724906314960249945105011301731247324601620886782967217339340393853616450077105125391982689986178342417223392217085276465471102737594719932347242482670320801063191869471318313514407997326350065187904154229557706351355052446027159972546737213451422978211055778164578782156428466626894026103053360431281644645515155471301826844754338802352846095293421718249819728205538534652212984831283642472071669494851823123552827380737798609829706225744376667082534026874483482483127491533474306552210039386256062116345785870668331513725792053302188276682550672663353937781055621860101624242216671635824311412793495965628876036344731733142759495348248970313655381407241457118743532311394697763283681852908564387282605279108
    
    p = Pollards_p_1(n, prod(primes))
    q = n // p
    
    print(long_to_bytes(standard_rsa_decryption(e, c, [p, q])))

    # b'NCTF{Th3r3_ar3_1ns3cure_RSA_m0duli_7hat_at_f1rst_gl4nce_appe4r_t0_be_s3cur3}'

4.14 [HDCTF2019]bbbbbbrsa

4.14.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
from base64 import b64encode as b32encode
from gmpy2 import invert,gcd,iroot
from Crypto.Util.number import *
from binascii import a2b_hex,b2a_hex
import random

flag = "******************************"

nbit = 128

p = getPrime(nbit)
q = getPrime(nbit)
n = p*q

print p
print n

phi = (p-1)*(q-1)

e = random.randint(50000,70000)

while True:
	if gcd(e,phi) == 1:
		break;
	else:
		e -= 1;

c = pow(int(b2a_hex(flag),16),e,n)

print b32encode(str(c))[::-1]

# 2373740699529364991763589324200093466206785561836101840381622237225512234632
# p = 177077389675257695042507998165006460849
# n = 37421829509887796274897162249367329400988647145613325367337968063341372726061
# c = ==gMzYDNzIjMxUTNyIzNzIjMyYTM4MDM0gTMwEjNzgTM2UTN4cjNwIjN2QzM5ADMwIDNyMTO4UzM2cTM5kDN2MTOyUTO5YDM0czM3MjM

4.14.2 解题思路

RSA 低公钥指数攻击：爆破小指数 $e$

4.14.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
import itertools
from gmpy2 import iroot
from base64 import b64decode
from Crypto.Util.number import long_to_bytes, GCD, inverse

def low_public_exponent_attack(n, c, e=None, lower=None, upper=None, phi=None):
    """
    RSA 低公钥指数攻击
    """
    if e is not None:
        # 小 e 且 m^e < n，可直接开 e 次方根
        for k in itertools.count():
            candidate = c + k * n
            root, exact = iroot(candidate, e)
            if exact:
                return int(root)
    elif phi is not None and lower is not None and upper is not None:
        # 若未知 e，则爆破 e，满足 gcd(e, φ) = 1 并计算 d
        for e_candidate in range(lower, upper):
            if GCD(e_candidate, phi) == 1:
                d = inverse(e_candidate, phi)
                m = pow(c, d, n)
                if b'flag' in long_to_bytes(m):
                    return m
    else:
        raise ValueError("参数不完整：请提供 e，或 (phi + low + high)")
    

if __name__ == '__main__':
    p = 177077389675257695042507998165006460849
    n = 37421829509887796274897162249367329400988647145613325367337968063341372726061
    c = b'==gMzYDNzIjMxUTNyIzNzIjMyYTM4MDM0gTMwEjNzgTM2UTN4cjNwIjN2QzM5ADMwIDNyMTO4UzM2cTM5kDN2MTOyUTO5YDM0czM3MjM'
    q = n // p

    ct = int(b64decode(c[::-1]))
    m = low_public_exponent_attack(n, ct, lower=50000, upper=70000, phi=(p-1)*(q-1))
    print(long_to_bytes(m))

    # b'flag{rs4_1s_s1mpl3!#}'

4.15 [BJDCTF2020]RSA4

4.15.1 题目

1
2
3
4
5
6
7
8
N = 331310324212000030020214312244232222400142410423413104441140203003243002104333214202031202212403400220031202142322434104143104244241214204444443323000244130122022422310201104411044030113302323014101331214303223312402430402404413033243132101010422240133122211400434023222214231402403403200012221023341333340042343122302113410210110221233241303024431330001303404020104442443120130000334110042432010203401440404010003442001223042211442001413004 
c = 310020004234033304244200421414413320341301002123030311202340222410301423440312412440240244110200112141140201224032402232131204213012303204422003300004011434102141321223311243242010014140422411342304322201241112402132203101131221223004022003120002110230023341143201404311340311134230140231412201333333142402423134333211302102413111111424430032440123340034044314223400401224111323000242234420441240411021023100222003123214343030122032301042243

N = 302240000040421410144422133334143140011011044322223144412002220243001141141114123223331331304421113021231204322233120121444434210041232214144413244434424302311222143224402302432102242132244032010020113224011121043232143221203424243134044314022212024343100042342002432331144300214212414033414120004344211330224020301223033334324244031204240122301242232011303211220044222411134403012132420311110302442344021122101224411230002203344140143044114 
c = 112200203404013430330214124004404423210041321043000303233141423344144222343401042200334033203124030011440014210112103234440312134032123400444344144233020130110134042102220302002413321102022414130443041144240310121020100310104334204234412411424420321211112232031121330310333414423433343322024400121200333330432223421433344122023012440013041401423202210124024431040013414313121123433424113113414422043330422002314144111134142044333404112240344

N = 332200324410041111434222123043121331442103233332422341041340412034230003314420311333101344231212130200312041044324431141033004333110021013020140020011222012300020041342040004002220210223122111314112124333211132230332124022423141214031303144444134403024420111423244424030030003340213032121303213343020401304243330001314023030121034113334404440421242240113103203013341231330004332040302440011324004130324034323430143102401440130242321424020323 
c = 10013444120141130322433204124002242224332334011124210012440241402342100410331131441303242011002101323040403311120421304422222200324402244243322422444414043342130111111330022213203030324422101133032212042042243101434342203204121042113212104212423330331134311311114143200011240002111312122234340003403312040401043021433112031334324322123304112340014030132021432101130211241134422413442312013042141212003102211300321404043012124332013240431242

4.15.2 解题思路

低加密指数广播攻击（Håstad’s Broadcast Attack）：$ m、e $ 相同，$ e = 3 $，多组加密的 $ n $ 和 $ c $

进制转换（五进制改为十进制）

4.15.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from gmpy2 import iroot, mpz
from functools import reduce
from Crypto.Util.number import inverse, long_to_bytes


def Håstad_broadcast_attack(ciphertexts, n, e=3):
    N = reduce(lambda x, y: x * y, (i for i in n))
    result = 0
    data = zip(ciphertexts, n)
    for ci, ni in data:
        Ni = N // ni
        di = inverse(Ni, ni)
        result += ci * Ni * di
    return iroot(mpz(result % N), e)[0]


if __name__ == '__main__':
    N1 = int('331310324212000030020214312244232222400142410423413104441140203003243002104333214202031202212403400220031202142322434104143104244241214204444443323000244130122022422310201104411044030113302323014101331214303223312402430402404413033243132101010422240133122211400434023222214231402403403200012221023341333340042343122302113410210110221233241303024431330001303404020104442443120130000334110042432010203401440404010003442001223042211442001413004',5)
    c1 = int('310020004234033304244200421414413320341301002123030311202340222410301423440312412440240244110200112141140201224032402232131204213012303204422003300004011434102141321223311243242010014140422411342304322201241112402132203101131221223004022003120002110230023341143201404311340311134230140231412201333333142402423134333211302102413111111424430032440123340034044314223400401224111323000242234420441240411021023100222003123214343030122032301042243',5)

    N2 = int('302240000040421410144422133334143140011011044322223144412002220243001141141114123223331331304421113021231204322233120121444434210041232214144413244434424302311222143224402302432102242132244032010020113224011121043232143221203424243134044314022212024343100042342002432331144300214212414033414120004344211330224020301223033334324244031204240122301242232011303211220044222411134403012132420311110302442344021122101224411230002203344140143044114',5)
    c2 = int('112200203404013430330214124004404423210041321043000303233141423344144222343401042200334033203124030011440014210112103234440312134032123400444344144233020130110134042102220302002413321102022414130443041144240310121020100310104334204234412411424420321211112232031121330310333414423433343322024400121200333330432223421433344122023012440013041401423202210124024431040013414313121123433424113113414422043330422002314144111134142044333404112240344',5)

    N3 = int('332200324410041111434222123043121331442103233332422341041340412034230003314420311333101344231212130200312041044324431141033004333110021013020140020011222012300020041342040004002220210223122111314112124333211132230332124022423141214031303144444134403024420111423244424030030003340213032121303213343020401304243330001314023030121034113334404440421242240113103203013341231330004332040302440011324004130324034323430143102401440130242321424020323',5)
    c3 = int('10013444120141130322433204124002242224332334011124210012440241402342100410331131441303242011002101323040403311120421304422222200324402244243322422444414043342130111111330022213203030324422101133032212042042243101434342203204121042113212104212423330331134311311114143200011240002111312122234340003403312040401043021433112031334324322123304112340014030132021432101130211241134422413442312013042141212003102211300321404043012124332013240431242',5)

    M = Håstad_broadcast_attack([c1, c2, c3], [N1, N2, N3])
    print(long_to_bytes(M))

    # b'noxCTF{D4mn_y0u_h4s74d_wh47_4_b100dy_b4s74rd!}'

4.16 [BJDCTF2020]rsa_output

4.16.1 题目

1
2
3
4
5
6
7
{21058339337354287847534107544613605305015441090508924094198816691219103399526800112802416383088995253908857460266726925615826895303377801614829364034624475195859997943146305588315939130777450485196290766249612340054354622516207681542973756257677388091926549655162490873849955783768663029138647079874278240867932127196686258800146911620730706734103611833179733264096475286491988063990431085380499075005629807702406676707841324660971173253100956362528346684752959937473852630145893796056675793646430793578265418255919376323796044588559726703858429311784705245069845938316802681575653653770883615525735690306674635167111,2767}

{21058339337354287847534107544613605305015441090508924094198816691219103399526800112802416383088995253908857460266726925615826895303377801614829364034624475195859997943146305588315939130777450485196290766249612340054354622516207681542973756257677388091926549655162490873849955783768663029138647079874278240867932127196686258800146911620730706734103611833179733264096475286491988063990431085380499075005629807702406676707841324660971173253100956362528346684752959937473852630145893796056675793646430793578265418255919376323796044588559726703858429311784705245069845938316802681575653653770883615525735690306674635167111,3659}

message1=20152490165522401747723193966902181151098731763998057421967155300933719378216342043730801302534978403741086887969040721959533190058342762057359432663717825826365444996915469039056428416166173920958243044831404924113442512617599426876141184212121677500371236937127571802891321706587610393639446868836987170301813018218408886968263882123084155607494076330256934285171370758586535415136162861138898728910585138378884530819857478609791126971308624318454905992919405355751492789110009313138417265126117273710813843923143381276204802515910527468883224274829962479636527422350190210717694762908096944600267033351813929448599

message2=11298697323140988812057735324285908480504721454145796535014418738959035245600679947297874517818928181509081545027056523790022598233918011261011973196386395689371526774785582326121959186195586069851592467637819366624044133661016373360885158956955263645614345881350494012328275215821306955212788282617812686548883151066866149060363482958708364726982908798340182288702101023393839781427386537230459436512613047311585875068008210818996941460156589314135010438362447522428206884944952639826677247819066812706835773107059567082822312300721049827013660418610265189288840247186598145741724084351633508492707755206886202876227

4.16.2 解题思路

共模攻击：若干次加密，$ e $ 不同，$ N $ 相同，$ m $ 相同

4.16.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from gmpy2 import gcdext
from Crypto.Util.number import long_to_bytes

def common_modulus_attack(e1, e2, c1, c2, n):
    _, r, s = gcdext(e1, e2)
    m = pow(c1, r, n) * pow(c2, s, n) % n
    return m


if __name__ == "__main__":
    n = 21058339337354287847534107544613605305015441090508924094198816691219103399526800112802416383088995253908857460266726925615826895303377801614829364034624475195859997943146305588315939130777450485196290766249612340054354622516207681542973756257677388091926549655162490873849955783768663029138647079874278240867932127196686258800146911620730706734103611833179733264096475286491988063990431085380499075005629807702406676707841324660971173253100956362528346684752959937473852630145893796056675793646430793578265418255919376323796044588559726703858429311784705245069845938316802681575653653770883615525735690306674635167111
    e1 = 2767
    e2 = 3659
    c1 = 20152490165522401747723193966902181151098731763998057421967155300933719378216342043730801302534978403741086887969040721959533190058342762057359432663717825826365444996915469039056428416166173920958243044831404924113442512617599426876141184212121677500371236937127571802891321706587610393639446868836987170301813018218408886968263882123084155607494076330256934285171370758586535415136162861138898728910585138378884530819857478609791126971308624318454905992919405355751492789110009313138417265126117273710813843923143381276204802515910527468883224274829962479636527422350190210717694762908096944600267033351813929448599
    c2 = 11298697323140988812057735324285908480504721454145796535014418738959035245600679947297874517818928181509081545027056523790022598233918011261011973196386395689371526774785582326121959186195586069851592467637819366624044133661016373360885158956955263645614345881350494012328275215821306955212788282617812686548883151066866149060363482958708364726982908798340182288702101023393839781427386537230459436512613047311585875068008210818996941460156589314135010438362447522428206884944952639826677247819066812706835773107059567082822312300721049827013660418610265189288840247186598145741724084351633508492707755206886202876227

    m = common_modulus_attack(e1, e2, c1, c2, n)
    print(long_to_bytes(m))

    # b'BJD{r3a_C0mmoN_moD@_4ttack}'

4.17 [BJDCTF2020]RSA

4.17.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from Crypto.Util.number import getPrime,bytes_to_long

flag=open("flag","rb").read()

p=getPrime(1024)
q=getPrime(1024)
assert(e<100000)
n=p*q
m=bytes_to_long(flag)
c=pow(m,e,n)
print c,n
print pow(294,e,n)

p=getPrime(1024)
n=p*q
m=bytes_to_long("BJD"*32)
c=pow(m,e,n)
print c,n

'''
output:
12641635617803746150332232646354596292707861480200207537199141183624438303757120570096741248020236666965755798009656547738616399025300123043766255518596149348930444599820675230046423373053051631932557230849083426859490183732303751744004874183062594856870318614289991675980063548316499486908923209627563871554875612702079100567018698992935818206109087568166097392314105717555482926141030505639571708876213167112187962584484065321545727594135175369233925922507794999607323536976824183162923385005669930403448853465141405846835919842908469787547341752365471892495204307644586161393228776042015534147913888338316244169120  13508774104460209743306714034546704137247627344981133461801953479736017021401725818808462898375994767375627749494839671944543822403059978073813122441407612530658168942987820256786583006947001711749230193542370570950705530167921702835627122401475251039000775017381633900222474727396823708695063136246115652622259769634591309421761269548260984426148824641285010730983215377509255011298737827621611158032976420011662547854515610597955628898073569684158225678333474543920326532893446849808112837476684390030976472053905069855522297850688026960701186543428139843783907624317274796926248829543413464754127208843070331063037
381631268825806469518166370387352035475775677163615730759454343913563615970881967332407709901235637718936184198930226303761876517101208677107311006065728014220477966000620964056616058676999878976943319063836649085085377577273214792371548775204594097887078898598463892440141577974544939268247818937936607013100808169758675042264568547764031628431414727922168580998494695800403043312406643527637667466318473669542326169218665366423043579003388486634167642663495896607282155808331902351188500197960905672207046579647052764579411814305689137519860880916467272056778641442758940135016400808740387144508156358067955215018
979153370552535153498477459720877329811204688208387543826122582132404214848454954722487086658061408795223805022202997613522014736983452121073860054851302343517756732701026667062765906277626879215457936330799698812755973057557620930172778859116538571207100424990838508255127616637334499680058645411786925302368790414768248611809358160197554369255458675450109457987698749584630551177577492043403656419968285163536823819817573531356497236154342689914525321673807925458651854768512396355389740863270148775362744448115581639629326362342160548500035000156097215446881251055505465713854173913142040976382500435185442521721  12806210903061368369054309575159360374022344774547459345216907128193957592938071815865954073287532545947370671838372144806539753829484356064919357285623305209600680570975224639214396805124350862772159272362778768036844634760917612708721787320159318432456050806227784435091161119982613987303255995543165395426658059462110056431392517548717447898084915167661172362984251201688639469652283452307712821398857016487590794996544468826705600332208535201443322267298747117528882985955375246424812616478327182399461709978893464093245135530135430007842223389360212803439850867615121148050034887767584693608776323252233254261047
'''

4.17.2 解题思路

模不互素：存在两个或更多模数 $ n $ 且其中至少一对 $ n_i $ 和 $ n_j $ 不互质

RSA 低公钥指数攻击：爆破小指数 $ e $

4.17.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
from math import prod
from sympy import totient
from base64 import b64decode
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
from Crypto.Util.number import long_to_bytes, GCD, inverse


def standard_rsa_decryption(e, c, primes=None, n=None, phi=None, ct_format='int'):
    """
    标准 RSA 解密
    """
    if not phi:
        if n:
            phi = totient(n)
        else:
            phi = prod(p - 1 for p in primes)
            n = prod(p for p in primes)

    d = inverse(e, phi)
    
    if ct_format == 'base64':
        p, q = primes[0], primes[1]
        key_info = RSA.construct((n, e, d, p, q))
        key = RSA.importKey(key_info.exportKey())
        key = PKCS1_OAEP.new(key)
        m = key.decrypt(b64decode(c)).decode()
    else:
        m = pow(c, d, n)

    return m


def non_coprime_moduli(n_list):
    """
    模不互素
    """
    result = []
    
    n = len(n_list)
    for i in range(n):
        for j in range(i + 1, n):  # j 从 i+1 开始，避免重复检查
            current_gcd = GCD(n_list[i], n_list[j])
            if current_gcd != 1:
                result.append((n_list[i], n_list[j], current_gcd))

    if result:
        print("找到不互质的模数对：")
        for i, j, gcd_val in result:
            print(f"模数 {i} 和模数 {j}, GCD = {gcd_val}")
    else:
        print("所有模数对均互质")

    return result


if __name__ == "__main__":
    c = 12641635617803746150332232646354596292707861480200207537199141183624438303757120570096741248020236666965755798009656547738616399025300123043766255518596149348930444599820675230046423373053051631932557230849083426859490183732303751744004874183062594856870318614289991675980063548316499486908923209627563871554875612702079100567018698992935818206109087568166097392314105717555482926141030505639571708876213167112187962584484065321545727594135175369233925922507794999607323536976824183162923385005669930403448853465141405846835919842908469787547341752365471892495204307644586161393228776042015534147913888338316244169120  
    n1 = 13508774104460209743306714034546704137247627344981133461801953479736017021401725818808462898375994767375627749494839671944543822403059978073813122441407612530658168942987820256786583006947001711749230193542370570950705530167921702835627122401475251039000775017381633900222474727396823708695063136246115652622259769634591309421761269548260984426148824641285010730983215377509255011298737827621611158032976420011662547854515610597955628898073569684158225678333474543920326532893446849808112837476684390030976472053905069855522297850688026960701186543428139843783907624317274796926248829543413464754127208843070331063037
    c_294 = 381631268825806469518166370387352035475775677163615730759454343913563615970881967332407709901235637718936184198930226303761876517101208677107311006065728014220477966000620964056616058676999878976943319063836649085085377577273214792371548775204594097887078898598463892440141577974544939268247818937936607013100808169758675042264568547764031628431414727922168580998494695800403043312406643527637667466318473669542326169218665366423043579003388486634167642663495896607282155808331902351188500197960905672207046579647052764579411814305689137519860880916467272056778641442758940135016400808740387144508156358067955215018
    c2 = 979153370552535153498477459720877329811204688208387543826122582132404214848454954722487086658061408795223805022202997613522014736983452121073860054851302343517756732701026667062765906277626879215457936330799698812755973057557620930172778859116538571207100424990838508255127616637334499680058645411786925302368790414768248611809358160197554369255458675450109457987698749584630551177577492043403656419968285163536823819817573531356497236154342689914525321673807925458651854768512396355389740863270148775362744448115581639629326362342160548500035000156097215446881251055505465713854173913142040976382500435185442521721  
    n2 = 12806210903061368369054309575159360374022344774547459345216907128193957592938071815865954073287532545947370671838372144806539753829484356064919357285623305209600680570975224639214396805124350862772159272362778768036844634760917612708721787320159318432456050806227784435091161119982613987303255995543165395426658059462110056431392517548717447898084915167661172362984251201688639469652283452307712821398857016487590794996544468826705600332208535201443322267298747117528882985955375246424812616478327182399461709978893464093245135530135430007842223389360212803439850867615121148050034887767584693608776323252233254261047
    q = non_coprime_moduli([n1, n2])[0][-1]
    p1 = n1 // q
    p2 = n2 // q
    
    for e in range(100000):
        if(pow(294, e, n1) == c_294):
            break
    print(long_to_bytes(standard_rsa_decryption(e, c, [p1, q])))

    # b'BJD{p_is_common_divisor}'

4.18 [WUSTCTF2020]babyrsa

4.18.1 题目

1
2
3
c = 28767758880940662779934612526152562406674613203406706867456395986985664083182
n = 73069886771625642807435783661014062604264768481735145873508846925735521695159
e = 65537

4.18.2 解题思路

大素数分解

4.18.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
import requests
from math import prod
from sympy import totient
from base64 import b64decode
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
from Crypto.Util.number import inverse, long_to_bytes

def queryFactors(n):
    """查询整数n的质因数分解结果"""
    response = requests.get(f"http://factordb.com/api?query={n}")
    return [int(factor) for factor, count in response.json()["factors"] for _ in range(int(count))]


def standard_rsa_decryption(e, c, primes=None, n=None, phi=None, ct_format='int'):
    """
    标准 RSA 解密
    """
    if not phi:
        if n:
            phi = totient(n)
        else:
            phi = prod(p - 1 for p in primes)
            n = prod(p for p in primes)

    d = inverse(e, phi)
    
    if ct_format == 'base64':
        p, q = primes[0], primes[1]
        key_info = RSA.construct((n, e, d, p, q))
        key = RSA.importKey(key_info.exportKey())
        key = PKCS1_OAEP.new(key)
        m = key.decrypt(b64decode(c)).decode()
    else:
        m = pow(c, d, n)

    return m

if __name__ == "__main__":
    c = 28767758880940662779934612526152562406674613203406706867456395986985664083182
    n = 73069886771625642807435783661014062604264768481735145873508846925735521695159
    e = 65537
    p, q = queryFactors(n)
    print(long_to_bytes(standard_rsa_decryption(e, c, [p, q])))

    # b'wctf2020{just_@_piece_0f_cak3}'

4.19 [ACTF新生赛2020]crypto-rsa3

4.19.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from flag import FLAG
from Cryptodome.Util.number import *
import gmpy2
import random

e=65537
p = getPrime(512)
q = int(gmpy2.next_prime(p))
n = p*q
m = bytes_to_long(FLAG)
c = pow(m,e,n)
print(n)
print(c)

177606504836499246970959030226871608885969321778211051080524634084516973331441644993898029573612290095853069264036530459253652875586267946877831055147546910227100566496658148381834683037366134553848011903251252726474047661274223137727688689535823533046778793131902143444408735610821167838717488859902242863683
1457390378511382354771000540945361168984775052693073641682375071407490851289703070905749525830483035988737117653971428424612332020925926617395558868160380601912498299922825914229510166957910451841730028919883807634489834128830801407228447221775264711349928156290102782374379406719292116047581560530382210049

4.19.2 解题思路

p、q 参数设置不当（近似攻击）

$ p $ 和 $ q $ 相邻，$ n^\frac{1}{2} $ 近似等于 $ p $，向下遍历求出 $ p $

4.19.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from Crypto.Util.number import long_to_bytes, inverse
from gmpy2 import iroot

def p_q_approximation(n, e, c):
    p = iroot(n,2)[0]
    while n % p != 0 :
        p -= 1
    
    q = n // p
    d = inverse(e, (p-1)*(q-1))
    return pow(c, d, n)


if __name__ == '__main__':
    n = 177606504836499246970959030226871608885969321778211051080524634084516973331441644993898029573612290095853069264036530459253652875586267946877831055147546910227100566496658148381834683037366134553848011903251252726474047661274223137727688689535823533046778793131902143444408735610821167838717488859902242863683
    c = 1457390378511382354771000540945361168984775052693073641682375071407490851289703070905749525830483035988737117653971428424612332020925926617395558868160380601912498299922825914229510166957910451841730028919883807634489834128830801407228447221775264711349928156290102782374379406719292116047581560530382210049
    e = 65537
    m = p_q_approximation(n, e, c)
    print(long_to_bytes(m))

    # b'actf{p_and_q_should_not_be_so_close_in_value}'

4.20 [GWCTF 2019]BabyRSA

4.20.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import hashlib
import sympy
from Crypto.Util.number import *

flag = 'GWHT{******}'
secret = '******'

assert(len(flag) == 38)

half = len(flag) / 2

flag1 = flag[:half]
flag2 = flag[half:]

secret_num = getPrime(1024) * bytes_to_long(secret)

p = sympy.nextprime(secret_num)
q = sympy.nextprime(p)

N = p * q

e = 0x10001

F1 = bytes_to_long(flag1)
F2 = bytes_to_long(flag2)

c1 = F1 + F2
c2 = pow(F1, 3) + pow(F2, 3)
assert(c2 < N)

m1 = pow(c1, e, N)
m2 = pow(c2, e, N)

output = open('secret', 'w')
output.write('N=' + str(N) + '\n')
output.write('m1=' + str(m1) + '\n')
output.write('m2=' + str(m2) + '\n')
output.close()

N=636585149594574746909030160182690866222909256464847291783000651837227921337237899651287943597773270944384034858925295744880727101606841413640006527614873110651410155893776548737823152943797884729130149758279127430044739254000426610922834573094957082589539445610828279428814524313491262061930512829074466232633130599104490893572093943832740301809630847541592548921200288222432789208650949937638303429456468889100192613859073752923812454212239908948930178355331390933536771065791817643978763045030833712326162883810638120029378337092938662174119747687899484603628344079493556601422498405360731958162719296160584042671057160241284852522913676264596201906163
m1=90009974341452243216986938028371257528604943208941176518717463554774967878152694586469377765296113165659498726012712288670458884373971419842750929287658640266219686646956929872115782173093979742958745121671928568709468526098715927189829600497283118051641107305128852697032053368115181216069626606165503465125725204875578701237789292966211824002761481815276666236869005129138862782476859103086726091860497614883282949955023222414333243193268564781621699870412557822404381213804026685831221430728290755597819259339616650158674713248841654338515199405532003173732520457813901170264713085107077001478083341339002069870585378257051150217511755761491021553239
m2=487443985757405173426628188375657117604235507936967522993257972108872283698305238454465723214226871414276788912058186197039821242912736742824080627680971802511206914394672159240206910735850651999316100014691067295708138639363203596244693995562780286637116394738250774129759021080197323724805414668042318806010652814405078769738548913675466181551005527065309515364950610137206393257148357659666687091662749848560225453826362271704292692847596339533229088038820532086109421158575841077601268713175097874083536249006018948789413238783922845633494023608865256071962856581229890043896939025613600564283391329331452199062858930374565991634191495137939574539546

4.20.2 解题思路

p、q 参数设置不当（近似攻击）：$ p $ 和 $ q $ 相邻，$ n^\frac{1}{2} $ 近似等于 $ p $，向下遍历求出 $ p $，进而求出 $ c_1 、 c_2 $。

已知 $ F_1 + F_2 $ 和 $ F_1^3 + F_2^3 $ 可求 $ F_1 、 F_2 $，证明：

$$
\begin{gathered}
F_1^3+F_2^3=(F_1+F_2)(F_1^2-F_1F_2+F_2^2)
\
将\ F_1+F_2=S\ 代入，得：T=S\cdot(F_1^2-F_1F_2+F_2^2)
\
\because F_1^2+F_2^2=(F_1+F_2)^2-2F_1F_2=S^2-2F_1F_2
\
\therefore T=S\cdot[(S^2-2F_1F_2)-F_1F_2]=S\cdot(S^2-3F_1F_2)=S^3-3S\cdot F_1F_2
\
\because S\neq0 \quad \therefore F_1F_2=\frac{S^3-T}{3S}
\
已知\ F_1 + F_2 = S\ 和\ F_1 F_2 = \frac{S^3-T}{3S}=P
\
F_1\ 和\ F_2\ 是一元二次方程的根：x^2 - Sx + P = 0
\
根据求根公式：x = \frac{S \pm \sqrt{S^2 - 4P}}{2}
\
得：F_1, F_2 = \frac{S \pm \sqrt{\frac{4T - S^3}{3S}}}{2}
\end{gathered}
$$

4.20.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
from Crypto.Util.number import long_to_bytes, inverse
from gmpy2 import iroot, isqrt


def p_q_approximation(n, e, c):
    p = iroot(n,2)[0]
    while n % p != 0 :
        p -= 1
    
    q = n // p
    d = inverse(e, (p-1)*(q-1))
    m = pow(c, d, n)
    return m


def solve_f1_f2(S, T):
    P = (S**3 - T) // (3 * S)
    delta = S**2 - 4 * P
    sqrt_d = isqrt(delta)
    x1 = (S + sqrt_d) // 2
    x2 = (S - sqrt_d) // 2
    return x1, x2


if __name__ == '__main__':
    n = 636585149594574746909030160182690866222909256464847291783000651837227921337237899651287943597773270944384034858925295744880727101606841413640006527614873110651410155893776548737823152943797884729130149758279127430044739254000426610922834573094957082589539445610828279428814524313491262061930512829074466232633130599104490893572093943832740301809630847541592548921200288222432789208650949937638303429456468889100192613859073752923812454212239908948930178355331390933536771065791817643978763045030833712326162883810638120029378337092938662174119747687899484603628344079493556601422498405360731958162719296160584042671057160241284852522913676264596201906163
    m1 = 90009974341452243216986938028371257528604943208941176518717463554774967878152694586469377765296113165659498726012712288670458884373971419842750929287658640266219686646956929872115782173093979742958745121671928568709468526098715927189829600497283118051641107305128852697032053368115181216069626606165503465125725204875578701237789292966211824002761481815276666236869005129138862782476859103086726091860497614883282949955023222414333243193268564781621699870412557822404381213804026685831221430728290755597819259339616650158674713248841654338515199405532003173732520457813901170264713085107077001478083341339002069870585378257051150217511755761491021553239
    m2 = 487443985757405173426628188375657117604235507936967522993257972108872283698305238454465723214226871414276788912058186197039821242912736742824080627680971802511206914394672159240206910735850651999316100014691067295708138639363203596244693995562780286637116394738250774129759021080197323724805414668042318806010652814405078769738548913675466181551005527065309515364950610137206393257148357659666687091662749848560225453826362271704292692847596339533229088038820532086109421158575841077601268713175097874083536249006018948789413238783922845633494023608865256071962856581229890043896939025613600564283391329331452199062858930374565991634191495137939574539546
    e = 0x10001
    c1 = p_q_approximation(n, e, m1)
    c2 = p_q_approximation(n, e, m2)
    f1, f2 = solve_f1_f2(c1, c2)
    flag = long_to_bytes(f1) + long_to_bytes(f2)
    print(flag)

    # b'GWHT{f709e0e2cfe7e530ca8972959a1033b2}'

4.21 SameMod

4.21.1 题目

1
2
3
4
5
{6266565720726907265997241358331585417095726146341989755538017122981360742813498401533594757088796536341941659691259323065631249,773}
{6266565720726907265997241358331585417095726146341989755538017122981360742813498401533594757088796536341941659691259323065631249,839}

message1=3453520592723443935451151545245025864232388871721682326408915024349804062041976702364728660682912396903968193981131553111537349
message2=5672818026816293344070119332536629619457163570036305296869053532293105379690793386019065754465292867769521736414170803238309535

4.21.2 解题思路

共模攻击

ASCII 码解码得 flag

4.21.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
from gmpy2 import gcdext, mpz
from Crypto.Util.number import long_to_bytes

def common_modulus_attack(e1, e2, c1, c2, n):
    _, r, s = gcdext(e1, e2)
    m = pow(c1, r, n) * pow(c2, s, n) % n
    return m

def ascii_decode(data):
    """
    解码连续拼接的 ASCII 数字字符串或整数为可读字符串。
    支持字符串、整数、或整数列表作为输入。
    """
    result = ""

    if isinstance(data, (int, mpz)):
        data = str(data)

    if isinstance(data, str):
        i = 0
        while i < len(data):
            for step in (3, 2):  # 尝试取3位再取2位
                chunk = data[i:i+step]
                if len(chunk) == step and chunk.isdigit():
                    val = int(chunk)
                    if 32 <= val <= 126:
                        result += chr(val)
                        i += step
                        break
            else:
                i += 1

    elif isinstance(data, list):
        result = ''.join(chr(x) for x in data if isinstance(x, int) and 32 <= x <= 126)

    return result

if __name__ == '__main__':
    n = 6266565720726907265997241358331585417095726146341989755538017122981360742813498401533594757088796536341941659691259323065631249
    e1 = 773
    e2 = 839
    message1 = 3453520592723443935451151545245025864232388871721682326408915024349804062041976702364728660682912396903968193981131553111537349
    message2 = 5672818026816293344070119332536629619457163570036305296869053532293105379690793386019065754465292867769521736414170803238309535

    m = common_modulus_attack(e1, e2, message1, message2, n)
    print(ascii_decode(m))

    # flag{whenwethinkitispossible}

4.22 [AFCTF2018]你能看出这是什么加密么

4.22.1 题目

1
2
3
4
5
6
7
p=0x928fb6aa9d813b6c3270131818a7c54edb18e3806942b88670106c1821e0326364194a8c49392849432b37632f0abe3f3c52e909b939c91c50e41a7b8cd00c67d6743b4f

q=0xec301417ccdffa679a8dcc4027dd0d75baf9d441625ed8930472165717f4732884c33f25d4ee6a6c9ae6c44aedad039b0b72cf42cab7f80d32b74061

e=0x10001

c=0x70c9133e1647e95c3cb99bd998a9028b5bf492929725a9e8e6d2e277fa0f37205580b196e5f121a2e83bc80a8204c99f5036a07c8cf6f96c420369b4161d2654a7eccbdaf583204b645e137b3bd15c5ce865298416fd5831cba0d947113ed5be5426b708b89451934d11f9aed9085b48b729449e461ff0863552149b965e22b6

4.22.2 解题思路

标准 RSA 解密

4.22.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
from math import prod
from sympy import totient
from base64 import b64decode
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
from Crypto.Util.number import inverse, long_to_bytes


def standard_rsa_decryption(e, c, primes=None, n=None, phi=None, ct_format='int'):
    """
    标准 RSA 解密
    """
    if not phi:
        if n:
            phi = totient(n)
        else:
            phi = prod(p - 1 for p in primes)
            n = prod(p for p in primes)

    d = inverse(e, phi)
    
    if ct_format == 'base64':
        p, q = primes[0], primes[1]
        key_info = RSA.construct((n, e, d, p, q))
        key = RSA.importKey(key_info.exportKey())
        key = PKCS1_OAEP.new(key)
        m = key.decrypt(b64decode(c)).decode()
    else:
        m = pow(c, d, n)

    return m


if __name__ == "__main__":
    p = 0x928fb6aa9d813b6c3270131818a7c54edb18e3806942b88670106c1821e0326364194a8c49392849432b37632f0abe3f3c52e909b939c91c50e41a7b8cd00c67d6743b4f
    q = 0xec301417ccdffa679a8dcc4027dd0d75baf9d441625ed8930472165717f4732884c33f25d4ee6a6c9ae6c44aedad039b0b72cf42cab7f80d32b74061
    e = 0x10001
    c = 0x70c9133e1647e95c3cb99bd998a9028b5bf492929725a9e8e6d2e277fa0f37205580b196e5f121a2e83bc80a8204c99f5036a07c8cf6f96c420369b4161d2654a7eccbdaf583204b645e137b3bd15c5ce865298416fd5831cba0d947113ed5be5426b708b89451934d11f9aed9085b48b729449e461ff0863552149b965e22b6

    print(long_to_bytes(standard_rsa_decryption(e, c, [p, q])))

    # b'afctf{R54_|5_$0_$imp13}'

4.23 [NCTF2019]babyRSA

4.23.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from Crypto.Util.number import *
from flag import flag

def nextPrime(n):
    n += 2 if n & 1 else 1
    while not isPrime(n):
        n += 2
    return n

p = getPrime(1024)
q = nextPrime(p)
n = p * q
e = 0x10001
d = inverse(e, (p-1) * (q-1))
c = pow(bytes_to_long(flag.encode()), e, n)

# d = 19275778946037899718035455438175509175723911466127462154506916564101519923603308900331427601983476886255849200332374081996442976307058597390881168155862238533018621944733299208108185814179466844504468163200369996564265921022888670062554504758512453217434777820468049494313818291727050400752551716550403647148197148884408264686846693842118387217753516963449753809860354047619256787869400297858568139700396567519469825398575103885487624463424429913017729585620877168171603444111464692841379661112075123399343270610272287865200880398193573260848268633461983435015031227070217852728240847398084414687146397303110709214913
# c = 5382723168073828110696168558294206681757991149022777821127563301413483223874527233300721180839298617076705685041174247415826157096583055069337393987892262764211225227035880754417457056723909135525244957935906902665679777101130111392780237502928656225705262431431953003520093932924375902111280077255205118217436744112064069429678632923259898627997145803892753989255615273140300021040654505901442787810653626524305706316663169341797205752938755590056568986738227803487467274114398257187962140796551136220532809687606867385639367743705527511680719955380746377631156468689844150878381460560990755652899449340045313521804

4.23.2 解题思路

p、q 参数设置不当（近似攻击）

已知 $ e $、$ d $、$ \phi(n) $ 或 $ n $ 的范围，求 n：
$$
\begin{gathered}
\because ed \equiv 1 \pmod {\phi(n)} \
\therefore ed=k \cdot \phi(n)+1
\end{gathered}
$$
$ ed-1 $ 长度为 2064 位，范围在 $2^{2063} \leq ed-1 \lt 2^{2064}$、并且 $\phi(n)$ 长度为 2048 位，范围在 $ 2^{2047} \leq \phi(n) \lt 2^{2048} $ 可爆破 $ k $（范围在$ \left\lceil\frac{2^{2063}}{2^{2048}}\right\rceil=\left\lceil2^{15}\right\rceil \lt k \lt \left\lceil\frac{2^{2064}}{2^{2047}}\right\rceil=\left\lceil2^{17}\right\rceil $）。

4.23.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from Crypto.Util.number import long_to_bytes
from gmpy2 import iroot, next_prime
from sympy import prevprime
    

if __name__ == "__main__":
    e = 65537
    d = 19275778946037899718035455438175509175723911466127462154506916564101519923603308900331427601983476886255849200332374081996442976307058597390881168155862238533018621944733299208108185814179466844504468163200369996564265921022888670062554504758512453217434777820468049494313818291727050400752551716550403647148197148884408264686846693842118387217753516963449753809860354047619256787869400297858568139700396567519469825398575103885487624463424429913017729585620877168171603444111464692841379661112075123399343270610272287865200880398193573260848268633461983435015031227070217852728240847398084414687146397303110709214913
    c = 5382723168073828110696168558294206681757991149022777821127563301413483223874527233300721180839298617076705685041174247415826157096583055069337393987892262764211225227035880754417457056723909135525244957935906902665679777101130111392780237502928656225705262431431953003520093932924375902111280077255205118217436744112064069429678632923259898627997145803892753989255615273140300021040654505901442787810653626524305706316663169341797205752938755590056568986738227803487467274114398257187962140796551136220532809687606867385639367743705527511680719955380746377631156468689844150878381460560990755652899449340045313521804
    ed = e*d - 1

    print(len(bin(ed)[2:]))
    # 2064

    for k in range(pow(2, 15), pow(2, 17)):
        if ed % k == 0:
            p = prevprime(iroot(ed // k, 2)[0])
            q = next_prime(p)
        
            if ed // k == (q-1)*(p-1):
                print(long_to_bytes(pow(c, d, p*q)))
                break

                # b'NCTF{70u2_nn47h_14_v3ry_gOO0000000d}'

4.24 [AFCTF2018]可怜的RSA

4.24.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
# flag.enc
GVd1d3viIXFfcHapEYuo5fAvIiUS83adrtMW/MgPwxVBSl46joFCQ1plcnlDGfL19K/3PvChV6n5QGohzfVyz2Z5GdTlaknxvHDUGf5HCukokyPwK/1EYU7NzrhGE7J5jPdi0Aj7xi/Odxy0hGMgpaBLd/nL3N8O6i9pc4Gg3O8soOlciBG/6/xdfN3SzSStMYIN8nfZZMSq3xDDvz4YB7TcTBh4ik4wYhuC77gmT+HWOv5gLTNQ3EkZs5N3EAopy11zHNYU80yv1jtFGcluNPyXYttU5qU33jcp0Wuznac+t+AZHeSQy5vk8DyWorSGMiS+J4KNqSVlDs12EqXEqqJ0uA==

# public.key
-----BEGIN PUBLIC KEY-----
MIIBJDANBgkqhkiG9w0BAQEFAAOCAREAMIIBDAKCAQMlsYv184kJfRcjeGa7Uc/4
3pIkU3SevEA7CZXJfA44bUbBYcrf93xphg2uR5HCFM+Eh6qqnybpIKl3g0kGA4rv
tcMIJ9/PP8npdpVE+U4Hzf4IcgOaOmJiEWZ4smH7LWudMlOekqFTs2dWKbqzlC59
NeMPfu9avxxQ15fQzIjhvcz9GhLqb373XDcn298ueA80KK6Pek+3qJ8YSjZQMrFT
+EJehFdQ6yt6vALcFc4CB1B6qVCGO7hICngCjdYpeZRNbGM/r6ED5Nsozof1oMbt
Si8mZEJ/Vlx3gathkUVtlxx/+jlScjdM7AFV5fkRidt0LkwosDoPoRz/sDFz0qTM
5q5TAgMBAAE=
-----END PUBLIC KEY-----

4.24.2 解题思路

提取公钥 + 大素数分解 + 标准 RSA 解密

4.24.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
import rsa
import requests
from math import prod
from sympy import totient
from base64 import b64decode
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
from Crypto.Util.number import inverse


class ExtractKey:
    @staticmethod
    def extract_public_key(pem_str):
        """
        提取 PEM 格式公钥中的 n（模数）和 e（公钥指数）
        """
        pubkey = rsa.PublicKey.load_pkcs1_openssl_pem(pem_str.encode())
        return pubkey.n, pubkey.e

    @staticmethod
    def extract_private_key(pem_str):
        """
        提取 PEM 格式私钥中的 n（模数）和 d（私钥指数）
        """
        privkey = rsa.PrivateKey.load_pkcs1(pem_str.encode())
        return privkey.n, privkey.d

def queryFactors(n):
    """查询整数n的质因数分解结果"""
    response = requests.get(f"http://factordb.com/api?query={n}")
    return [int(factor) for factor, count in response.json()["factors"] for _ in range(int(count))]


def standard_rsa_decryption(e, c, primes=None, n=None, phi=None, ct_format='int'):
    """
    标准 RSA 解密
    """
    if not phi:
        if n:
            phi = totient(n)
        else:
            phi = prod(p - 1 for p in primes)
            n = prod(p for p in primes)

    d = inverse(e, phi)
    
    if ct_format == 'base64':
        p, q = primes[0], primes[1]
        key_info = RSA.construct((n, e, d, p, q))
        key = RSA.importKey(key_info.exportKey())
        key = PKCS1_OAEP.new(key)
        m = key.decrypt(b64decode(c)).decode()
    else:
        m = pow(c, d, n)

    return m

if __name__ == "__main__":
    public_pem = """-----BEGIN PUBLIC KEY-----
    MIIBJDANBgkqhkiG9w0BAQEFAAOCAREAMIIBDAKCAQMlsYv184kJfRcjeGa7Uc/4
    3pIkU3SevEA7CZXJfA44bUbBYcrf93xphg2uR5HCFM+Eh6qqnybpIKl3g0kGA4rv
    tcMIJ9/PP8npdpVE+U4Hzf4IcgOaOmJiEWZ4smH7LWudMlOekqFTs2dWKbqzlC59
    NeMPfu9avxxQ15fQzIjhvcz9GhLqb373XDcn298ueA80KK6Pek+3qJ8YSjZQMrFT
    +EJehFdQ6yt6vALcFc4CB1B6qVCGO7hICngCjdYpeZRNbGM/r6ED5Nsozof1oMbt
    Si8mZEJ/Vlx3gathkUVtlxx/+jlScjdM7AFV5fkRidt0LkwosDoPoRz/sDFz0qTM
    5q5TAgMBAAE=
    -----END PUBLIC KEY-----"""

    n, e = ExtractKey.extract_public_key(public_pem)
    p, q = queryFactors(n)

    ct = b'GVd1d3viIXFfcHapEYuo5fAvIiUS83adrtMW/MgPwxVBSl46joFCQ1plcnlDGfL19K/3PvChV6n5QGohzfVyz2Z5GdTlaknxvHDUGf5HCukokyPwK/1EYU7NzrhGE7J5jPdi0Aj7xi/Odxy0hGMgpaBLd/nL3N8O6i9pc4Gg3O8soOlciBG/6/xdfN3SzSStMYIN8nfZZMSq3xDDvz4YB7TcTBh4ik4wYhuC77gmT+HWOv5gLTNQ3EkZs5N3EAopy11zHNYU80yv1jtFGcluNPyXYttU5qU33jcp0Wuznac+t+AZHeSQy5vk8DyWorSGMiS+J4KNqSVlDs12EqXEqqJ0uA=='
    m = standard_rsa_decryption(e, ct, [p, q], ct_format='base64')
    print(m)

    # afctf{R54_|5_$0_B0rin9}

4.25 [网鼎杯 2020 青龙组]you_raise_me_up

4.25.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from Crypto.Util.number import *
import random

n = 2 ** 512
m = random.randint(2, n-1) | 1
c = pow(m, bytes_to_long(flag), n)
print 'm = ' + str(m)
print 'c = ' + str(c)

# m = 391190709124527428959489662565274039318305952172936859403855079581402770986890308469084735451207885386318986881041563704825943945069343345307381099559075
# c = 6665851394203214245856789450723658632520816791621796775909766895233000234023642878786025644953797995373211308485605397024123180085924117610802485972584499

4.25.2 解题思路

已知较小 $ m、n、c $ 求 $ e $

4.25.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from Crypto.Util.number import long_to_bytes
from sympy.ntheory import discrete_log

def m_n_c(m, n, c):
    return discrete_log(n, c, m)


if __name__ == '__main__':
    n = 2 ** 512
    m = 391190709124527428959489662565274039318305952172936859403855079581402770986890308469084735451207885386318986881041563704825943945069343345307381099559075
    c = 6665851394203214245856789450723658632520816791621796775909766895233000234023642878786025644953797995373211308485605397024123180085924117610802485972584499
    print(long_to_bytes(m_n_c(m, n, c)))

    # b'flag{5f95ca93-1594-762d-ed0b-a9139692cb4a}'

4.26 RSA & what

4.26.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
# README.txt
素数生成算法太麻烦了，有没有取巧的方法呢？
诶，这里好像有个不错的想法哟。
看起来节约了不少时间呢，嘿嘿嘿……
顺便问问，应该大家都知道base64吧，用来编码还是很方便的呢！

# HUB1
785095419718268286866508214304816985447077293766819398728046411166917810820484759314291028976498223661229395009474063173705162627037610993539617751905443039278227583504604808251931083818909467613277587874545761074364427549966555519371913859875313577282243053150056274667798049694695703660313532933165449312949725581708965417273055582216295994587600975970124811496270080896977076946000102701030260990598181466447208054713391526313700681341093922240317428173599031624125155188216489476825606191521182034969120343287691181300399683515414809262700457525876691808180257730351707673660380698973884642306898810000633684878715402823143549139850732982897459698089649561190746850698130299458080255582312696873149210028240898137822888492559957665067936573356367589784593119016624072433872744537432005911668494455733330689385141214653091888017782049043434862620306783436169856564175929871100669913438980899219579329897753233450934770193915434791427728636586218049874617231705308003720066269312729135764175698611068808404054125581540114956463603240222497919384691718744014002554201602395969312999994159599536026359879060218056496345745457493919771337601177449899066579857630036350871090452649830775029695488575574985078428560054253180863725364147
1697

412629526163150748619328091306742267675740578011800062477174189782151273970783531227579758540364970485350157944321579108232221072397135934034064481497887079641131808838242743811511451355024436983050572020925065644355566434625618133203024215941534926113892937988520918939061441606915556516246057349589921494351383160036280826024605351878408056180907759973804117263002554923041750587548819746346813966673034182913325507826219961923932100526305289894965216608254252188398580139545189681875824089456195044984585824938384521905334289906422454152976834867304693292466676355760173232407753256256317546190171995276258924613533179898467683358934751999655196790168438343198229183747091108262988777659858609744709324571850262293294975336628234767258858873839342596887193772615000676401522431518310648303975593582965021189182246986957349253156736526071639973844039068996404290548474640668851856078201093335425412842295604919065487301340901573809617549185106072798799159726375235125260509158832996701927878713084753334549129580912412168594170659605421750204835970231909591063407612779337478065175988365401590396247576709343727196106058477166945670117868989025903023998142850338956985816131805349549059377047477131270847579095628384569645636821650
494644347943710545224678831941589086572700792465459558770782213550069709458568349686998660541810166872034041584767487150140111151788221460027897193248273461607411027815984883969396220626358625041781558277804930212654296704055890683796941327712758797770820006623289146990000114915293539639766846910274034245607746230740851938158390562286057002223177609606376329007676845450142537930798148258428701466415483232670659815791064681384406494388237742330786225557303988025468036820082959712050733095860546860468575857084616069132051094882919253745234762029759124776348047587755897123575123506976140900565238840752841856713613368250071926171873213897914794115466890719123299469964019450899291410760762179836946570945555295288184698184555018368687708432612286248476073758067175481771199066581572870175460016017100414479346437034291784837132240891321931601494414908927713208448927221095745802380014441841139882391378410438764884597938773868771896252329517440068673532468372840830510218585255432000690265226016573313570977945083879214961394087065558376158826938257664840570952233832852869328785568175434516247720356520242602299510374317488182738732700078879665745909603766482100138001417023680647717824323143388857817595766172152883484274718248
152942283599728307168144137370127212672611894072038732126041098102628831053000986759260271210671922070555948023688596575415822984026159010574404359474670428678518262175033880513984372909748992727828381694416776740981021730545374002974037896534944567124543272737618380646771071804878796585983783360553761828325817820260204820004421979881871027255562690952334900616675606524933557440263648233514757200263521499508373975003431306847453046714027687108396945719803444444954079308404947126216395526551292104722047878178373207886033071857277857997932255251315982837892164421298202073945919187779856785892717251746704537315003771369737854896595170485152591013676942418134278534037654467840633528916812275267230155352077736583130992587670941654695382287023971261529987384520843829695778029311786431227409189019205818351911572757145556993606643464336196802350204616056286497246016800105003143046120608673496196758720552776772796609670537056331996894322779267635281472481559819839042424017171718303214059720568484939239370144038161541354254182769979771948759413102933987773401644506930205164891773826513161783736386604783484446345744957119469799231796368324927570694496679453313927562345656690240414624431304646248599226046524702364131095964335
79717988936247951265489157583697956031893477858854186991051529161879478488281744062318600470906120960002282886511477294555606503083169449335174864424180701080203993329996226566203834693869525797695969610065991941396723959032680019082506816443041598300477625793433080664346470586416385854692124426348587211026568667694805849554780794033764714016521711467557284846737236374990121316809833819996821592832639024026411520407330206281265390130763948165694574512140518775603040182029818771866749548761938870605590174330887949847420877829240131490902432602005681085180807294176837646062568094875766945890382971790015490163385088144673549085079635083262975154206269679142412897438231719704933258660779310737302680265445437771977749959110744959368586293082016067927548564967400845992380076107522755566531760628823374519718763740378295585535591752887339222947397184116326706799921515431185636740825707782742373783475781052674257292910213843986132987466810027275052416774693363446184518901899202502828670309452622347532932678874990809930682575738653876289384151496807194146308614368821006660626870989784697045160231069428458961107751207771093777394616856305293335603892178327520756554333365975114235981173451368131680404850832773147333013716920
123111353650401158556639983459870663057297871992927053886971224773529636525110628183715748795987525113177540092814119928708272290370336537110381023134637759740716140969662183269370676630325583385284994943164692397459103195434968057377474610500216801375394703781249039351368816958227409657934091741509357152328382960684515093945552479461382281913961956745154260686029997827565075768703774895750561575155143606297116391666385705899138085693913246313778033627210312268959737394553510894720099165193981333775907531107232556909478156441457899797515694348816961762796703443502856101079430585547997496001098926600499728389113862894833789669213630332988693669889340482430613291490613803204484751470676686041002772556117213612152322606737150858116122936539131795111263513114569794532805886643087299918196635113037777138666914296986040549274559835214505300618256105508764026461518876579387159881983544667258537064954616097750399839661065797883103731694314852301848272092388637114950059216922969842082648527035538090054093890365647676119748995243416337805666557501345234056968476142608491830438065401219751688687373709390057521910942736632126729711606256158399963682990881473178216060827021373776598901281958527655543318413664277921492723185984
36869806815936046911848195817405817350259890871483063184373728397968909458432625046025376290214729914038387534731762237978339011724858818860181178811639468996206294711495853807311240013786226884265118119546377272154555615363105236192878292703331473547623021744317034819416624562896226194523639793573028006666236271812390759036235867495803255905843636447252225413871038762657801345647584493917576263471587347202664391908570140389126903204602391093990827188675090199750617303773574821926387194478875191828814971296674530519321530805302667925998711835019806761133078403281404889374663875077339168901297819436499920958268483684335998301056068380228873524800383911402490807139268964095165069610454677558808756444381542173782815227920906224931028457073652453777424387873533280455944646592996920617956675786286711447540353883400282402551158169958389450168079568459656526911857835375748015814860506707921852997096156275804955989964215077733621769938075413007804223217091604613132253046399456747595300404564172224333936405545921819654435437072133387523533568472443532200069133022979195685683508297337961701169394794966256415112246587706103819620428258245999539040721929317130088874161577093962579487428358736401687123174207198251449851429295

# HUB2
785095419718268286866508214304816985447077293766819398728046411166917810820484759314291028976498223661229395009474063173705162627037610993539617751905443039278227583504604808251931083818909467613277587874545761074364427549966555519371913859875313577282243053150056274667798049694695703660313532933165449312949725581708965417273055582216295994587600975970124811496270080896977076946000102701030260990598181466447208054713391526313700681341093922240317428173599031624125155188216489476825606191521182034969120343287691181300399683515414809262700457525876691808180257730351707673660380698973884642306898810000633684878715402823143549139850732982897459698089649561190746850698130299458080255582312696873149210028240898137822888492559957665067936573356367589784593119016624072433872744537432005911668494455733330689385141214653091888017782049043434862620306783436169856564175929871100669913438980899219579329897753233450934770193915434791427728636586218049874617231705308003720066269312729135764175698611068808404054125581540114956463603240222497919384691718744014002554201602395969312999994159599536026359879060218056496345745457493919771337601177449899066579857630036350871090452649830775029695488575574985078428560054253180863725364147
599

592169079372093727306100216011395857825646323934289480976073629037543922902098120901138454462177159996376654176248238979132528728327590301098966139983157980612320563496546128644967731000716697705104079039156276714872147463350811303393260622707024952543509891692246246277965823414460326811240048060543656588688604452353899779068825120910282167004715339763187734797180326976132213325054697165320479166356562518029805927741656605174809726397565772271562066078076105491745903986597877400370206718954975288721072048333678609055008135809089304229015364348490924974097403734627265297637171818849461766523691595241613878709865506436588268999163342945070495338153600520537498539457396582804692959296612715752573140296135784933206146091436617979599749774330699946637591406356289409716084034451049094715202196203486088368791744107629271647320273259836915312794297246589501008666299165717722507702866033454215783240025504356157664454861755286285777763585177751796252655008206383024707883077513745863312079349790275094080707502392866946325796914450602264462588722052297430827681750827349094323968337670311272933785838850649376115667223821665435911506351891489985627506615492005617098615432522564204152887767244129985681083657783356557756654335186
373940646416832740878733255707567753033716583448402000789202767511920210382830343955553654111486728333980557319799362514960627879016797491389812007768832730979916230647641872759001906846747977631675704310179448857128160385701185892914523053669366534408863734305635222625590986006420486092550427301086984563126480814987024980594613542978310129247678826691418335300577577527951623696426435497835228167084738007750914270251001921329521479047662848650808989996085600197309361410863238526802127877523767262921515150984998560136647154865791163316503073285223966216441025637452229043510097323724381056976302288136843260163922706692913035222445496716008888946581535004546355744211680390731257309941902587303353139951102244865270295414474488798335404630458489706639805186573874814586736746232358849677477533671968344154242963289415569487579895910660999043578737461300406937828924818002658292769882181668784501439254131996848948120781562158861495883827848139425862249576454689133681009549361314460818658995959098228995702202268649635363105549975932395335076521137604288520082040121286614922986554652700056148966514178935952363036963217619879899671383604638416567950421350546204434902113156720006282720889591288850271076074941927715678306057176
527630926460622936571385649841758214453416849039412401087443444317101857090904711485538107058823056085840539073345920792871368232355475394571098380596835468509997340505604333730547799560998822989747473780307779717715522787724471724766494090783971030594671013168209717686720448579582618378459567979027822271918653169622428153856198907810040224340270362413432495029672123261375400927159831537760709974778708160583252613784358234858583174544777979242887938827573604837766801998381379999076416444683891078093889686055482709838668356120916040352123019019255084513769603803814947774554028717814638951416291274696771515474086351482107953150253616922787262398450376249126999644026382478413080973933173079111305142716133389111399235545279259017424722601848670061556859163943895466553927946412523750166582734005733378328468250568944945912238495877929717101722314678120172228493787964904072583905721074766711732215815561012960394537195757832959268603775112932862105945720853959285187521763557915356428113876893276879775603217718981852114599706699524551973934242045743122744146361596971245034059345915315495232135483464496114770357536576200511490922413208178149869347802988786513451486411409887164516065062084917556120712465074206435831498113605
8786437178698940322877889807009957616777351844979869726962356553244050911283984280960665761649310895230455072977431415102053987735969326553978994853162483051544656873294555116009995592043183070208706258164840540599577072097104139505857517663273929851202628854185356185647194933800084230503413037858893307713037149307477830536758283681093517617820169181420796105338681582230788318108428132051793761014952837330456262272828627355701464740578197966332613127307037255647286823496355917642353327912440019621838870388091824748629637425759125214639885130163183752378908729773517053259212525494555880921052679512582051516604297098204363525081039382358483926727008679327719083138865969291911863630382097160230960738043575559330264018212774424527719153248563876760067931499029384228993253862501939337758514377472011933279273181144830381169849387893799390755052093069179605579485710343655570028592595882436632426527654452895431758715126580164902410286422637215098476316042367916779431052267545769495994723721129943616294879642305545894912914632980455031755879087401575310699765408473606166727137934224515998416625122213056208800095077933103150699272650116151674702438463062734472714004926103668378506804002740045547964716693536349447660850580
205314962204511500352858372254132533167549960825498949618514841570703199264867431580754674275990554478140637041427842111391746883257447120035947621456863890934062044010795443059281736346976175772415034838334682726635263432655537852942177334888025283748611576171534251461847349566505628290587224150869640386437623371249743165260396675220683302142805646368906930575140628610003919131999295855501215111393294818218799982703289304596989070475000081175510085432290264502023736899104746316830742226946395027029820825791831870857382647221322734605026210073093918331247494307555600335550942340526536281372036612138713881098866303169425501998978400008829873080965592009371176208668290074288903681417933657472279670688597862835627506340169978450918788539270346340385928840299573889292189531738082166408734046381423516467694328971385421907314814283489322619386570046183556572383980777277173349209330683424343658179781015072259378576130442222984963071166207642585589822061597282467850868050737957726423713761694231879497037175627546427449730638216214828463003483408928375620315193290871300316930139260521382533279767663839278693750409419493280753368451508802658272220767624766390639285308433607255253282702383762149755935518922075584637512494819
271453634732502613378948161256470991260052778799128789839624515809143527363206813219580098196957510291648493698144497567392065251244844074992734669490296293997386198359280316655904691639367482203210051809125904410431506925238374843856343243276508280641059690938930957474434518308646618959004216831130099873532714372402117796666560677624822509159287675432413016478948594640872091688482149004426363946048517480052906306290126242866034249478040406351940088231081456109195799442996799641647167552689564613346415247906852055588498305665928450828756152103096629274760601528737639415361467941349982213641454967962723875032638267311935042334584913897338553953961877439389588793074211502597238465542889335363559052368180212013206172712561221352833891640659020253527584706465205486408990762759230842192028381048563437724528409174790022752557512795782713125166158329880702730769957185428522011430144840232256419113631679343171680631630775266488738173707357123139368825087043785842169049943237537188129367275730984789479909103397937113837824575137021012333461552176687570010445744268373840742899299977372834041925102853718964831225250407279578465008537542659673685686242773379131904890865110699190451534445434533919127658976874721029586168106207

# RSA.py
from Crypto.Util.number import bytes_to_long, getPrime
from random import randint
from gmpy2 import powmod

p = getPrime(2048)
q = getPrime(2048)
N = p*q
Phi = (p-1)*(q-1)
def get_enc_key(N,Phi):
    e = getPrime(N)
    if Phi % e == 0:
        return get_enc_key(N, Phi)
    else:
        return e
e1 = get_enc_key(randint(10, 12), Phi)
e2 = get_enc_key(randint(10, 12), Phi)

fr = open(r"./base64", "rb")#flag is in this file
f1 = open(r"./HUB1", "wb")
f2 = open(r"./HUB2", "wb")
base64 = fr.read(255)
f1.write("%d\n%d\n" % (N, e1))
f2.write("%d\n%d\n" % (N, e2))
while len(base64)>0:
    pt = bytes_to_long(base64)
    ct1 = powmod(pt, e1, N)
    ct2 = powmod(pt, e2, N)
    f1.write("\n%d" % ct1)
    f2.write("\n%d" % ct2)
    base64 = fr.read(255)
fr.close()
f1.close()
f2.close()

4.26.2 解题思路

共模攻击 + Base64 隐写

4.26.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
import gmpy2
import base64
from Crypto.Util.number import long_to_bytes

def common_modulus_attack(e1, e2, c1, c2, n):
    _, r, s = gmpy2.gcdext(e1, e2)
    m = pow(c1, r, n) * pow(c2, s, n) % n
    return m


class Base64Steganography:
    def __init__(self):
        # Base64 字符集，用于定位字符索引
        self.base64_chars = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/'

    def text_to_binary(self, text):
        """将文本转为二进制字符串"""
        return ''.join(f"{ord(c):08b}" for c in text)

    def binary_to_text(self, binary_str):
        """将二进制字符串转为文本"""
        return ''.join(chr(int(binary_str[i:i+8], 2)) for i in range(0, len(binary_str), 8))

    def read_base64_lines(self, content: bytes):
        """
        读取并解析 Base64 明文，按行分割
        """
        return content.strip().split(b'\n')

    def encode(self, plaintext: bytes, secret_text: str) -> bytes:
        """
        将秘密信息编码进 Base64 明文中
        """
        binary_secret = self.text_to_binary(secret_text)
        result_lines = []

        lines = self.read_base64_lines(plaintext)
        for line in lines:
            line = line.rstrip(b'\n')
            encoded = base64.b64encode(line)
            pad_count = encoded.count(b'=')

            if pad_count and binary_secret:
                usable_bits = min(pad_count * 2, len(binary_secret))
                bits = binary_secret[:usable_bits]
                binary_secret = binary_secret[usable_bits:]

                offset = int(bits, 2)
                pos = len(encoded) - pad_count - 1

                old_char = encoded[pos:pos+1]
                old_index = self.base64_chars.index(old_char.decode())
                new_index = (old_index + offset) % 64
                new_char = self.base64_chars[new_index].encode()

                encoded = encoded[:pos] + new_char + encoded[pos+1:]

            result_lines.append(encoded)

        return b'\n'.join(result_lines)

    def decode(self, stego_text: bytes) -> str:
        """
        从 Base64 明文中提取秘密信息
        """
        binary_secret = ''
        lines = self.read_base64_lines(stego_text)

        for line in lines:
            stego = line.strip()
            try:
                decoded = base64.b64decode(stego)
                original = base64.b64encode(decoded)
            except Exception:
                continue  # 忽略非法行

            if not stego.rstrip(b'='):
                continue

            stego_char = stego.rstrip(b'=')[-1:]
            orig_char = original.rstrip(b'=')[-1:]

            s_idx = self.base64_chars.index(stego_char.decode())
            o_idx = self.base64_chars.index(orig_char.decode())
            offset = (s_idx - o_idx) % 64

            pad_count = stego.count(b'=')
            if pad_count:
                binary_secret += f"{offset:0{pad_count * 2}b}"

        return self.binary_to_text(binary_secret)


if __name__ == '__main__':
    N = 785095419718268286866508214304816985447077293766819398728046411166917810820484759314291028976498223661229395009474063173705162627037610993539617751905443039278227583504604808251931083818909467613277587874545761074364427549966555519371913859875313577282243053150056274667798049694695703660313532933165449312949725581708965417273055582216295994587600975970124811496270080896977076946000102701030260990598181466447208054713391526313700681341093922240317428173599031624125155188216489476825606191521182034969120343287691181300399683515414809262700457525876691808180257730351707673660380698973884642306898810000633684878715402823143549139850732982897459698089649561190746850698130299458080255582312696873149210028240898137822888492559957665067936573356367589784593119016624072433872744537432005911668494455733330689385141214653091888017782049043434862620306783436169856564175929871100669913438980899219579329897753233450934770193915434791427728636586218049874617231705308003720066269312729135764175698611068808404054125581540114956463603240222497919384691718744014002554201602395969312999994159599536026359879060218056496345745457493919771337601177449899066579857630036350871090452649830775029695488575574985078428560054253180863725364147
    e1 = 1697
    e2 = 599
    ct1 = [
        412629526163150748619328091306742267675740578011800062477174189782151273970783531227579758540364970485350157944321579108232221072397135934034064481497887079641131808838242743811511451355024436983050572020925065644355566434625618133203024215941534926113892937988520918939061441606915556516246057349589921494351383160036280826024605351878408056180907759973804117263002554923041750587548819746346813966673034182913325507826219961923932100526305289894965216608254252188398580139545189681875824089456195044984585824938384521905334289906422454152976834867304693292466676355760173232407753256256317546190171995276258924613533179898467683358934751999655196790168438343198229183747091108262988777659858609744709324571850262293294975336628234767258858873839342596887193772615000676401522431518310648303975593582965021189182246986957349253156736526071639973844039068996404290548474640668851856078201093335425412842295604919065487301340901573809617549185106072798799159726375235125260509158832996701927878713084753334549129580912412168594170659605421750204835970231909591063407612779337478065175988365401590396247576709343727196106058477166945670117868989025903023998142850338956985816131805349549059377047477131270847579095628384569645636821650,
        494644347943710545224678831941589086572700792465459558770782213550069709458568349686998660541810166872034041584767487150140111151788221460027897193248273461607411027815984883969396220626358625041781558277804930212654296704055890683796941327712758797770820006623289146990000114915293539639766846910274034245607746230740851938158390562286057002223177609606376329007676845450142537930798148258428701466415483232670659815791064681384406494388237742330786225557303988025468036820082959712050733095860546860468575857084616069132051094882919253745234762029759124776348047587755897123575123506976140900565238840752841856713613368250071926171873213897914794115466890719123299469964019450899291410760762179836946570945555295288184698184555018368687708432612286248476073758067175481771199066581572870175460016017100414479346437034291784837132240891321931601494414908927713208448927221095745802380014441841139882391378410438764884597938773868771896252329517440068673532468372840830510218585255432000690265226016573313570977945083879214961394087065558376158826938257664840570952233832852869328785568175434516247720356520242602299510374317488182738732700078879665745909603766482100138001417023680647717824323143388857817595766172152883484274718248,
        152942283599728307168144137370127212672611894072038732126041098102628831053000986759260271210671922070555948023688596575415822984026159010574404359474670428678518262175033880513984372909748992727828381694416776740981021730545374002974037896534944567124543272737618380646771071804878796585983783360553761828325817820260204820004421979881871027255562690952334900616675606524933557440263648233514757200263521499508373975003431306847453046714027687108396945719803444444954079308404947126216395526551292104722047878178373207886033071857277857997932255251315982837892164421298202073945919187779856785892717251746704537315003771369737854896595170485152591013676942418134278534037654467840633528916812275267230155352077736583130992587670941654695382287023971261529987384520843829695778029311786431227409189019205818351911572757145556993606643464336196802350204616056286497246016800105003143046120608673496196758720552776772796609670537056331996894322779267635281472481559819839042424017171718303214059720568484939239370144038161541354254182769979771948759413102933987773401644506930205164891773826513161783736386604783484446345744957119469799231796368324927570694496679453313927562345656690240414624431304646248599226046524702364131095964335,
        79717988936247951265489157583697956031893477858854186991051529161879478488281744062318600470906120960002282886511477294555606503083169449335174864424180701080203993329996226566203834693869525797695969610065991941396723959032680019082506816443041598300477625793433080664346470586416385854692124426348587211026568667694805849554780794033764714016521711467557284846737236374990121316809833819996821592832639024026411520407330206281265390130763948165694574512140518775603040182029818771866749548761938870605590174330887949847420877829240131490902432602005681085180807294176837646062568094875766945890382971790015490163385088144673549085079635083262975154206269679142412897438231719704933258660779310737302680265445437771977749959110744959368586293082016067927548564967400845992380076107522755566531760628823374519718763740378295585535591752887339222947397184116326706799921515431185636740825707782742373783475781052674257292910213843986132987466810027275052416774693363446184518901899202502828670309452622347532932678874990809930682575738653876289384151496807194146308614368821006660626870989784697045160231069428458961107751207771093777394616856305293335603892178327520756554333365975114235981173451368131680404850832773147333013716920,
        123111353650401158556639983459870663057297871992927053886971224773529636525110628183715748795987525113177540092814119928708272290370336537110381023134637759740716140969662183269370676630325583385284994943164692397459103195434968057377474610500216801375394703781249039351368816958227409657934091741509357152328382960684515093945552479461382281913961956745154260686029997827565075768703774895750561575155143606297116391666385705899138085693913246313778033627210312268959737394553510894720099165193981333775907531107232556909478156441457899797515694348816961762796703443502856101079430585547997496001098926600499728389113862894833789669213630332988693669889340482430613291490613803204484751470676686041002772556117213612152322606737150858116122936539131795111263513114569794532805886643087299918196635113037777138666914296986040549274559835214505300618256105508764026461518876579387159881983544667258537064954616097750399839661065797883103731694314852301848272092388637114950059216922969842082648527035538090054093890365647676119748995243416337805666557501345234056968476142608491830438065401219751688687373709390057521910942736632126729711606256158399963682990881473178216060827021373776598901281958527655543318413664277921492723185984,
        36869806815936046911848195817405817350259890871483063184373728397968909458432625046025376290214729914038387534731762237978339011724858818860181178811639468996206294711495853807311240013786226884265118119546377272154555615363105236192878292703331473547623021744317034819416624562896226194523639793573028006666236271812390759036235867495803255905843636447252225413871038762657801345647584493917576263471587347202664391908570140389126903204602391093990827188675090199750617303773574821926387194478875191828814971296674530519321530805302667925998711835019806761133078403281404889374663875077339168901297819436499920958268483684335998301056068380228873524800383911402490807139268964095165069610454677558808756444381542173782815227920906224931028457073652453777424387873533280455944646592996920617956675786286711447540353883400282402551158169958389450168079568459656526911857835375748015814860506707921852997096156275804955989964215077733621769938075413007804223217091604613132253046399456747595300404564172224333936405545921819654435437072133387523533568472443532200069133022979195685683508297337961701169394794966256415112246587706103819620428258245999539040721929317130088874161577093962579487428358736401687123174207198251449851429295
    ]
    ct2 = [
        592169079372093727306100216011395857825646323934289480976073629037543922902098120901138454462177159996376654176248238979132528728327590301098966139983157980612320563496546128644967731000716697705104079039156276714872147463350811303393260622707024952543509891692246246277965823414460326811240048060543656588688604452353899779068825120910282167004715339763187734797180326976132213325054697165320479166356562518029805927741656605174809726397565772271562066078076105491745903986597877400370206718954975288721072048333678609055008135809089304229015364348490924974097403734627265297637171818849461766523691595241613878709865506436588268999163342945070495338153600520537498539457396582804692959296612715752573140296135784933206146091436617979599749774330699946637591406356289409716084034451049094715202196203486088368791744107629271647320273259836915312794297246589501008666299165717722507702866033454215783240025504356157664454861755286285777763585177751796252655008206383024707883077513745863312079349790275094080707502392866946325796914450602264462588722052297430827681750827349094323968337670311272933785838850649376115667223821665435911506351891489985627506615492005617098615432522564204152887767244129985681083657783356557756654335186,
        373940646416832740878733255707567753033716583448402000789202767511920210382830343955553654111486728333980557319799362514960627879016797491389812007768832730979916230647641872759001906846747977631675704310179448857128160385701185892914523053669366534408863734305635222625590986006420486092550427301086984563126480814987024980594613542978310129247678826691418335300577577527951623696426435497835228167084738007750914270251001921329521479047662848650808989996085600197309361410863238526802127877523767262921515150984998560136647154865791163316503073285223966216441025637452229043510097323724381056976302288136843260163922706692913035222445496716008888946581535004546355744211680390731257309941902587303353139951102244865270295414474488798335404630458489706639805186573874814586736746232358849677477533671968344154242963289415569487579895910660999043578737461300406937828924818002658292769882181668784501439254131996848948120781562158861495883827848139425862249576454689133681009549361314460818658995959098228995702202268649635363105549975932395335076521137604288520082040121286614922986554652700056148966514178935952363036963217619879899671383604638416567950421350546204434902113156720006282720889591288850271076074941927715678306057176,
        527630926460622936571385649841758214453416849039412401087443444317101857090904711485538107058823056085840539073345920792871368232355475394571098380596835468509997340505604333730547799560998822989747473780307779717715522787724471724766494090783971030594671013168209717686720448579582618378459567979027822271918653169622428153856198907810040224340270362413432495029672123261375400927159831537760709974778708160583252613784358234858583174544777979242887938827573604837766801998381379999076416444683891078093889686055482709838668356120916040352123019019255084513769603803814947774554028717814638951416291274696771515474086351482107953150253616922787262398450376249126999644026382478413080973933173079111305142716133389111399235545279259017424722601848670061556859163943895466553927946412523750166582734005733378328468250568944945912238495877929717101722314678120172228493787964904072583905721074766711732215815561012960394537195757832959268603775112932862105945720853959285187521763557915356428113876893276879775603217718981852114599706699524551973934242045743122744146361596971245034059345915315495232135483464496114770357536576200511490922413208178149869347802988786513451486411409887164516065062084917556120712465074206435831498113605,
        8786437178698940322877889807009957616777351844979869726962356553244050911283984280960665761649310895230455072977431415102053987735969326553978994853162483051544656873294555116009995592043183070208706258164840540599577072097104139505857517663273929851202628854185356185647194933800084230503413037858893307713037149307477830536758283681093517617820169181420796105338681582230788318108428132051793761014952837330456262272828627355701464740578197966332613127307037255647286823496355917642353327912440019621838870388091824748629637425759125214639885130163183752378908729773517053259212525494555880921052679512582051516604297098204363525081039382358483926727008679327719083138865969291911863630382097160230960738043575559330264018212774424527719153248563876760067931499029384228993253862501939337758514377472011933279273181144830381169849387893799390755052093069179605579485710343655570028592595882436632426527654452895431758715126580164902410286422637215098476316042367916779431052267545769495994723721129943616294879642305545894912914632980455031755879087401575310699765408473606166727137934224515998416625122213056208800095077933103150699272650116151674702438463062734472714004926103668378506804002740045547964716693536349447660850580,
        205314962204511500352858372254132533167549960825498949618514841570703199264867431580754674275990554478140637041427842111391746883257447120035947621456863890934062044010795443059281736346976175772415034838334682726635263432655537852942177334888025283748611576171534251461847349566505628290587224150869640386437623371249743165260396675220683302142805646368906930575140628610003919131999295855501215111393294818218799982703289304596989070475000081175510085432290264502023736899104746316830742226946395027029820825791831870857382647221322734605026210073093918331247494307555600335550942340526536281372036612138713881098866303169425501998978400008829873080965592009371176208668290074288903681417933657472279670688597862835627506340169978450918788539270346340385928840299573889292189531738082166408734046381423516467694328971385421907314814283489322619386570046183556572383980777277173349209330683424343658179781015072259378576130442222984963071166207642585589822061597282467850868050737957726423713761694231879497037175627546427449730638216214828463003483408928375620315193290871300316930139260521382533279767663839278693750409419493280753368451508802658272220767624766390639285308433607255253282702383762149755935518922075584637512494819,
        271453634732502613378948161256470991260052778799128789839624515809143527363206813219580098196957510291648493698144497567392065251244844074992734669490296293997386198359280316655904691639367482203210051809125904410431506925238374843856343243276508280641059690938930957474434518308646618959004216831130099873532714372402117796666560677624822509159287675432413016478948594640872091688482149004426363946048517480052906306290126242866034249478040406351940088231081456109195799442996799641647167552689564613346415247906852055588498305665928450828756152103096629274760601528737639415361467941349982213641454967962723875032638267311935042334584913897338553953961877439389588793074211502597238465542889335363559052368180212013206172712561221352833891640659020253527584706465205486408990762759230842192028381048563437724528409174790022752557512795782713125166158329880702730769957185428522011430144840232256419113631679343171680631630775266488738173707357123139368825087043785842169049943237537188129367275730984789479909103397937113837824575137021012333461552176687570010445744268373840742899299977372834041925102853718964831225250407279578465008537542659673685686242773379131904890865110699190451534445434533919127658976874721029586168106207
    ]

    m = b''
    for i in range(len(ct1)):
        m += (long_to_bytes(common_modulus_attack(e1, e2, ct1[i], ct2[i], N)))
    pt = Base64Steganography().decode(m)
    print(f"flag{{{pt}}}")

    # flag{7c86d8f7d6de33a87f7f9d6b005ce640}

4.27 [NPUCTF2020]EzRSA

4.27.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from gmpy2 import lcm , powmod , invert , gcd , mpz
from Crypto.Util.number import getPrime
from sympy import nextprime
from random import randint
p = getPrime(1024)
q = getPrime(1024)
n = p * q
gift = lcm(p - 1 , q - 1)
e = 54722
flag = b'NPUCTF{******************}'
m = int.from_bytes(flag , 'big')
c = powmod(m , e , n)
print('n: ' , n)
print('gift: ' , gift)
print('c: ' , c)

#n:  17083941230213489700426636484487738282426471494607098847295335339638177583685457921198569105417734668692072727759139358207667248703952436680183153327606147421932365889983347282046439156176685765143620637107347870401946946501620531665573668068349080410807996582297505889946205052879002028936125315312256470583622913646319779125559691270916064588684997382451412747432722966919513413709987353038375477178385125453567111965259721484997156799355617642131569095810304077131053588483057244340742751804935494087687363416921314041547093118565767609667033859583125275322077617576783247853718516166743858265291135353895239981121
#gift:  2135492653776686212553329560560967285303308936825887355911916917454772197960682240149821138177216833586509090969892419775958406087994054585022894165950768427741545736247918410255804894522085720642952579638418483800243368312702566458196708508543635051350999572787188236243275631609875253617015664414032058822919469443284453403064076232765024248435543326597418851751586308514540124571309152787559712950209357825576896132278045112177910266019741013995106579484868768251084453338417115483515132869594712162052362083414163954681306259137057581036657441897428432575924018950961141822554251369262248368899977337886190114104
#c:  3738960639194737957667684143565005503596276451617922474669745529299929395507971435311181578387223323429323286927370576955078618335757508161263585164126047545413028829873269342924092339298957635079736446851837414357757312525158356579607212496060244403765822636515347192211817658170822313646743520831977673861869637519843133863288550058359429455052676323196728280408508614527953057214779165450356577820378810467527006377296194102671360302059901897977339728292345132827184227155061326328585640019916328847372295754472832318258636054663091475801235050657401857262960415898483713074139212596685365780269667500271108538319

4.27.2 解题思路

$ \phi(n) $ 与 $ e $ 不互素

最大公约数和最小公倍数关系：$ \text{lcm}(a , b) \times \text{gcd}(a, b)=a \cdot b $，因为 $ n $ 长度为 2048 位，$ \phi(n) $ 长度 $ \leq n $，最小公倍数长度为 2045 位，所以最大公约数长度为 2-3 位，可爆破。

4.27.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from Crypto.Util.number import inverse, long_to_bytes, GCD
from gmpy2 import iroot


def e_phi_not_coprime(phi, e, n, c):
    '''
    phi(n) 与 e 不互素
    '''
    _gcd = GCD(e, phi)
    d = inverse(e//_gcd, phi)
    m = pow(c, d, n)
    return iroot(m, _gcd)[0]


if __name__ == '__main__':
    e = 54722
    n = 17083941230213489700426636484487738282426471494607098847295335339638177583685457921198569105417734668692072727759139358207667248703952436680183153327606147421932365889983347282046439156176685765143620637107347870401946946501620531665573668068349080410807996582297505889946205052879002028936125315312256470583622913646319779125559691270916064588684997382451412747432722966919513413709987353038375477178385125453567111965259721484997156799355617642131569095810304077131053588483057244340742751804935494087687363416921314041547093118565767609667033859583125275322077617576783247853718516166743858265291135353895239981121
    gift = 2135492653776686212553329560560967285303308936825887355911916917454772197960682240149821138177216833586509090969892419775958406087994054585022894165950768427741545736247918410255804894522085720642952579638418483800243368312702566458196708508543635051350999572787188236243275631609875253617015664414032058822919469443284453403064076232765024248435543326597418851751586308514540124571309152787559712950209357825576896132278045112177910266019741013995106579484868768251084453338417115483515132869594712162052362083414163954681306259137057581036657441897428432575924018950961141822554251369262248368899977337886190114104
    c = 3738960639194737957667684143565005503596276451617922474669745529299929395507971435311181578387223323429323286927370576955078618335757508161263585164126047545413028829873269342924092339298957635079736446851837414357757312525158356579607212496060244403765822636515347192211817658170822313646743520831977673861869637519843133863288550058359429455052676323196728280408508614527953057214779165450356577820378810467527006377296194102671360302059901897977339728292345132827184227155061326328585640019916328847372295754472832318258636054663091475801235050657401857262960415898483713074139212596685365780269667500271108538319
    
    for g in range(2, 8):
        phi = gift * g
        try:
            m = e_phi_not_coprime(phi, e, n, c)
            print(long_to_bytes(m))
            break
        except:
            continue
    
    # b'NPUCTF{diff1cult_rsa_1s_e@sy}'

4.28 [MRCTF2020]babyRSA

4.28.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
import sympy
import random
from gmpy2 import gcd, invert
from Crypto.Util.number import getPrime, isPrime, getRandomNBitInteger, bytes_to_long, long_to_bytes
from z3 import *
flag = b"MRCTF{xxxx}"
base = 65537


def GCD(A):
    B = 1
    for i in range(1, len(A)):
        B = gcd(A[i-1], A[i])
    return B


def gen_p():
    P = [0 for i in range(17)]
    P[0] = getPrime(128)
    for i in range(1, 17):
        P[i] = sympy.nextprime(P[i-1])
    print("P_p :", P[9])
    n = 1
    for i in range(17):
        n *= P[i]
    p = getPrime(1024)
    factor = pow(p, base, n)
    print("P_factor :", factor)
    return sympy.nextprime(p)


def gen_q():
    sub_Q = getPrime(1024)
    Q_1 = getPrime(1024)
    Q_2 = getPrime(1024)
    Q = sub_Q ** Q_2 % Q_1
    print("Q_1: ", Q_1)
    print("Q_2: ", Q_2)
    print("sub_Q: ", sub_Q)
    return sympy.nextprime(Q)


if __name__ == "__main__":
    _E = base
    _P = gen_p()
    _Q = gen_q()
    assert (gcd(_E, (_P - 1) * (_Q - 1)) == 1)
    _M = bytes_to_long(flag)
    _C = pow(_M, _E, _P * _Q)
    print("Ciphertext = ", _C)
'''
P_p : 206027926847308612719677572554991143421
P_factor : 213671742765908980787116579976289600595864704574134469173111790965233629909513884704158446946409910475727584342641848597858942209151114627306286393390259700239698869487469080881267182803062488043469138252786381822646126962323295676431679988602406971858136496624861228526070581338082202663895710929460596143281673761666804565161435963957655012011051936180536581488499059517946308650135300428672486819645279969693519039407892941672784362868653243632727928279698588177694171797254644864554162848696210763681197279758130811723700154618280764123396312330032986093579531909363210692564988076206283296967165522152288770019720928264542910922693728918198338839
Q_1:  103766439849465588084625049495793857634556517064563488433148224524638105971161051763127718438062862548184814747601299494052813662851459740127499557785398714481909461631996020048315790167967699932967974484481209879664173009585231469785141628982021847883945871201430155071257803163523612863113967495969578605521
Q_2:  151010734276916939790591461278981486442548035032350797306496105136358723586953123484087860176438629843688462671681777513652947555325607414858514566053513243083627810686084890261120641161987614435114887565491866120507844566210561620503961205851409386041194326728437073995372322433035153519757017396063066469743
sub_Q:  168992529793593315757895995101430241994953638330919314800130536809801824971112039572562389449584350643924391984800978193707795909956472992631004290479273525116959461856227262232600089176950810729475058260332177626961286009876630340945093629959302803189668904123890991069113826241497783666995751391361028949651
Ciphertext =  1709187240516367141460862187749451047644094885791761673574674330840842792189795049968394122216854491757922647656430908587059997070488674220330847871811836724541907666983042376216411561826640060734307013458794925025684062804589439843027290282034999617915124231838524593607080377300985152179828199569474241678651559771763395596697140206072537688129790126472053987391538280007082203006348029125729650207661362371936196789562658458778312533505938858959644541233578654340925901963957980047639114170033936570060250438906130591377904182111622236567507022711176457301476543461600524993045300728432815672077399879668276471832
'''

4.28.2 解题思路

计算多因数欧拉函数 + 标准 RSA 解密

4.28.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
from math import prod
from base64 import b64decode
from collections import Counter
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
from sympy import totient, nextprime, prevprime
from Crypto.Util.number import inverse, long_to_bytes


def euler_totient_from_factors(prime_factors):
    """
    根据质因数列表计算欧拉函数 φ(n)
    """
    if not prime_factors:
        return 1  # 处理 n=1 的情况
    
    # 统计每个质因数的指数
    factors_count = Counter(prime_factors)
    
    # 计算 n
    n = 1
    for p, k in factors_count.items():
        n *= p ** k
    
    # 计算 φ(n) = n × ∏(1 - 1/p)
    phi = n
    for p in factors_count:
        phi = phi // p * (p - 1)
    
    return phi


def standard_rsa_decryption(e, c, primes=None, n=None, phi=None, ct_format='int'):
    """
    标准 RSA 解密
    """
    if not phi:
        if n:
            phi = totient(n)
        else:
            phi = prod(p - 1 for p in primes)
            n = prod(p for p in primes)

    d = inverse(e, phi)
    
    if ct_format == 'base64':
        p, q = primes[0], primes[1]
        key_info = RSA.construct((n, e, d, p, q))
        key = RSA.importKey(key_info.exportKey())
        key = PKCS1_OAEP.new(key)
        m = key.decrypt(b64decode(c)).decode()
    else:
        m = pow(c, d, n)

    return m



if __name__ == '__main__':
    e = 65537
    P_p = 206027926847308612719677572554991143421
    P_factor = 213671742765908980787116579976289600595864704574134469173111790965233629909513884704158446946409910475727584342641848597858942209151114627306286393390259700239698869487469080881267182803062488043469138252786381822646126962323295676431679988602406971858136496624861228526070581338082202663895710929460596143281673761666804565161435963957655012011051936180536581488499059517946308650135300428672486819645279969693519039407892941672784362868653243632727928279698588177694171797254644864554162848696210763681197279758130811723700154618280764123396312330032986093579531909363210692564988076206283296967165522152288770019720928264542910922693728918198338839
    Q_1 = 103766439849465588084625049495793857634556517064563488433148224524638105971161051763127718438062862548184814747601299494052813662851459740127499557785398714481909461631996020048315790167967699932967974484481209879664173009585231469785141628982021847883945871201430155071257803163523612863113967495969578605521
    Q_2 = 151010734276916939790591461278981486442548035032350797306496105136358723586953123484087860176438629843688462671681777513652947555325607414858514566053513243083627810686084890261120641161987614435114887565491866120507844566210561620503961205851409386041194326728437073995372322433035153519757017396063066469743
    sub_Q = 168992529793593315757895995101430241994953638330919314800130536809801824971112039572562389449584350643924391984800978193707795909956472992631004290479273525116959461856227262232600089176950810729475058260332177626961286009876630340945093629959302803189668904123890991069113826241497783666995751391361028949651
    Ciphertext = 1709187240516367141460862187749451047644094885791761673574674330840842792189795049968394122216854491757922647656430908587059997070488674220330847871811836724541907666983042376216411561826640060734307013458794925025684062804589439843027290282034999617915124231838524593607080377300985152179828199569474241678651559771763395596697140206072537688129790126472053987391538280007082203006348029125729650207661362371936196789562658458778312533505938858959644541233578654340925901963957980047639114170033936570060250438906130591377904182111622236567507022711176457301476543461600524993045300728432815672077399879668276471832

    P_list = [0 for i in range(17)]
    P_list[9] = P_p
    for i in range(10, 17):
        P_list[i] = nextprime(P_list[i-1])
    for i in range(8, -1, -1):
        P_list[i] = prevprime(P_list[i+1])

    n = prod(P_list)
    phi = euler_totient_from_factors(P_list)
    d_p = inverse(e, phi)
    p = nextprime(pow(P_factor, d_p, n))
    print(p)

    Q = pow(sub_Q, Q_2, Q_1)
    q = nextprime(Q)
    print(q)

    print(long_to_bytes(standard_rsa_decryption(e, Ciphertext, [p, q])))

    # b'MRCTF{sti11_@_b@by_qu3st10n}'

4.29 [WUSTCTF2020]情书

4.29.1 题目

1
2
3
4
5
6
7
Premise: Enumerate the alphabet by 0、1、2、.....  、25
Using the RSA system 
Encryption:0156 0821 1616 0041 0140 2130 1616 0793
Public Key:2537 and 13
Private Key:2537 and 937

flag: wctf2020{Decryption}

4.29.2 解题思路

标准 RSA 解密 + 自定义码表替换

4.29.3 解题脚本

1
2
3
4
5
6
7
8
if __name__ == "__main__":
    n = 2537
    d = 937
    ct_list = '0156 0821 1616 0041 0140 2130 1616 0793'.split()
    pt = ''.join(chr(pow(int(ct), d, n) + ord('a')) for ct in ct_list)
    print(f'flag{{{pt}}}')
    
    # flag{iloveyou}

4.30 [WUSTCTF2020]dp_leaking_1s_very_d@angerous

4.30.1 题目

1
2
3
4
e = 65537
n = 156808343598578774957375696815188980682166740609302831099696492068246337198792510898818496239166339015207305102101431634283168544492984586566799996471150252382144148257236707247267506165670877506370253127695314163987084076462560095456635833650720606337852199362362120808707925913897956527780930423574343287847
c = 108542078809057774666748066235473292495343753790443966020636060807418393737258696352569345621488958094856305865603100885838672591764072157183336139243588435583104423268921439473113244493821692560960443688048994557463526099985303667243623711454841573922233051289561865599722004107134302070301237345400354257869
dp = 734763139918837027274765680404546851353356952885439663987181004382601658386317353877499122276686150509151221546249750373865024485652349719427182780275825

4.30.2 解题思路

$ dp、dq $ 泄露

已知 $ dp、n、e、c $，求 $ m $

4.30.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from Crypto.Util.number import inverse, long_to_bytes

def dp_n_e_c(dp: int, e: int, n: int, c: int) -> bytes:
    """
    已知 dp (dq)、n、e、c，求明文 m
    """
    # 遍历可能的k值，寻找有效的p
    for k in range(1, e):
        if (dp * e - 1) % k: continue
        p = ((dp * e - 1) // k) + 1
        if n % p: continue
        q = n // p
        d = inverse(e, (p - 1) * (q - 1))
        return pow(c, d, n)


if __name__ == "__main__":
    e = 65537
    n = 156808343598578774957375696815188980682166740609302831099696492068246337198792510898818496239166339015207305102101431634283168544492984586566799996471150252382144148257236707247267506165670877506370253127695314163987084076462560095456635833650720606337852199362362120808707925913897956527780930423574343287847
    c = 108542078809057774666748066235473292495343753790443966020636060807418393737258696352569345621488958094856305865603100885838672591764072157183336139243588435583104423268921439473113244493821692560960443688048994557463526099985303667243623711454841573922233051289561865599722004107134302070301237345400354257869
    dp = 734763139918837027274765680404546851353356952885439663987181004382601658386317353877499122276686150509151221546249750373865024485652349719427182780275825

    m = dp_n_e_c(dp, e, n, c)
    print(long_to_bytes(m))

    # b'wctf2020{dp_leaking_1s_very_d@angerous}'

4.31 [MRCTF2020]Easy_RSA

4.31.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
import sympy
from gmpy2 import gcd, invert
from random import randint
from Crypto.Util.number import getPrime, isPrime, getRandomNBitInteger, bytes_to_long, long_to_bytes
import base64

from zlib import *
flag = b"MRCTF{XXXX}"
base = 65537

def gen_prime(N):
    A = 0
    while 1:
        A = getPrime(N)
        if A % 8 == 5:
            break
    return A

def gen_p():
    p = getPrime(1024)
    q = getPrime(1024)
    assert (p < q)
    n = p * q
    print("P_n = ", n)
    F_n = (p - 1) * (q - 1)
    print("P_F_n = ", F_n)
    factor2 = 2021 * p + 2020 * q
    if factor2 < 0:
        factor2 = (-1) * factor2
    return sympy.nextprime(factor2)


def gen_q():
    p = getPrime(1024)
    q = getPrime(1024)
    assert (p < q)
    n = p * q
    print("Q_n = ", n)
    e = getRandomNBitInteger(53)
    F_n = (p - 1) * (q - 1)
    while gcd(e, F_n) != 1:
        e = getRandomNBitInteger(53)
    d = invert(e, F_n)
    print("Q_E_D = ", e * d)
    factor2 = 2021 * p - 2020 * q
    if factor2 < 0:
        factor2 = (-1) * factor2
    return sympy.nextprime(factor2)


if __name__ == "__main__":
    _E = base
    _P = gen_p()
    _Q = gen_q()
    assert (gcd(_E, (_P - 1) * (_Q - 1)) == 1)
    _M = bytes_to_long(flag)
    _C = pow(_M, _E, _P * _Q)
    print("Ciphertext = ", _C)
'''
P_n =  14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024336556028267742021320891681762543660468484018686865891073110757394154024833552558863671537491089957038648328973790692356014778420333896705595252711514117478072828880198506187667924020260600124717243067420876363980538994101929437978668709128652587073901337310278665778299513763593234951137512120572797739181693
P_F_n =  14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024099427363967321110127562039879018616082926935567951378185280882426903064598376668106616694623540074057210432790309571018778281723710994930151635857933293394780142192586806292968028305922173313521186946635709194350912242693822450297748434301924950358561859804256788098033426537956252964976682327991427626735740
Q_n =  20714298338160449749545360743688018842877274054540852096459485283936802341271363766157976112525034004319938054034934880860956966585051684483662535780621673316774842614701726445870630109196016676725183412879870463432277629916669130494040403733295593655306104176367902352484367520262917943100467697540593925707162162616635533550262718808746254599456286578409187895171015796991910123804529825519519278388910483133813330902530160448972926096083990208243274548561238253002789474920730760001104048093295680593033327818821255300893423412192265814418546134015557579236219461780344469127987669565138930308525189944897421753947
Q_E_D =  100772079222298134586116156850742817855408127716962891929259868746672572602333918958075582671752493618259518286336122772703330183037221105058298653490794337885098499073583821832532798309513538383175233429533467348390389323225198805294950484802068148590902907221150968539067980432831310376368202773212266320112670699737501054831646286585142281419237572222713975646843555024731855688573834108711874406149540078253774349708158063055754932812675786123700768288048445326199880983717504538825498103789304873682191053050366806825802602658674268440844577955499368404019114913934477160428428662847012289516655310680119638600315228284298935201
Ciphertext =  40855937355228438525361161524441274634175356845950884889338630813182607485910094677909779126550263304194796000904384775495000943424070396334435810126536165332565417336797036611773382728344687175253081047586602838685027428292621557914514629024324794275772522013126464926990620140406412999485728750385876868115091735425577555027394033416643032644774339644654011686716639760512353355719065795222201167219831780961308225780478482467294410828543488412258764446494815238766185728454416691898859462532083437213793104823759147317613637881419787581920745151430394526712790608442960106537539121880514269830696341737507717448946962021
'''

4.31.2 解题思路

求 $ P $：已知 $ n 、 \phi(n) $，求 $p、q$

求 $ Q $：已知 $e 、 d 、 n$，求 $p 、 q$

标准 RSA 解密

4.31.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
import random
from math import prod
from gmpy2 import iroot
from base64 import b64decode
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
from sympy import totient, nextprime
from Crypto.Util.number import inverse, long_to_bytes, GCD


def standard_rsa_decryption(e, c, primes=None, n=None, phi=None, ct_format='int'):
    """
    标准 RSA 解密
    """
    if not phi:
        if n:
            phi = totient(n)
        else:
            phi = prod(p - 1 for p in primes)
            n = prod(p for p in primes)

    d = inverse(e, phi)
    
    if ct_format == 'base64':
        p, q = primes[0], primes[1]
        key_info = RSA.construct((n, e, d, p, q))
        key = RSA.importKey(key_info.exportKey())
        key = PKCS1_OAEP.new(key)
        m = key.decrypt(b64decode(c)).decode()
    else:
        m = pow(c, d, n)

    return m


def phi_n(n, phi):
    """
    已知 n、phi(n)，求 p 和 q
    """
    # 计算 p + q
    s = n - phi + 1
    
    # 计算判别式
    discriminant = s * s - 4 * n
    sqrt_d = iroot(discriminant, 2)
    if not sqrt_d[1]:
        return None  # 不是完全平方数，无整数解
    
    # x^2 - (p + q)x + n = 0
    sqrt_d = int(sqrt_d[0])
    p = (s - sqrt_d) // 2
    q = (s + sqrt_d) // 2
    
    # 验证是否满足条件
    if p * q == n:
        return (p, q)
    else:
        return None


def n_e_d(n, ed):
    """
    已知 d, e, n 恢复质数因子 p 和 q
    """
    while True:
        k = ed - 1
        g = random.randint(2, n - 1)  # 避免0和1
        
        # 分解k为2^r * t
        t = k
        while t % 2 == 0:
            t //= 2
        
        # 寻找非平凡平方根
        y = pow(g, t, n)
        if y == 1 or y == n - 1:
            continue
            
        for _ in range(k.bit_length()):  # 最多尝试r次
            prev_y = y
            y = pow(y, 2, n)
            
            if y == 1:
                p = GCD(prev_y - 1, n)
                if p != 1 and p != n:
                    q = n // p
                    return (p, q)
                break
                
            if y == n - 1:
                break


if __name__ == "__main__":
    e = 65537
    P_n = 14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024336556028267742021320891681762543660468484018686865891073110757394154024833552558863671537491089957038648328973790692356014778420333896705595252711514117478072828880198506187667924020260600124717243067420876363980538994101929437978668709128652587073901337310278665778299513763593234951137512120572797739181693
    P_F_n = 14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024099427363967321110127562039879018616082926935567951378185280882426903064598376668106616694623540074057210432790309571018778281723710994930151635857933293394780142192586806292968028305922173313521186946635709194350912242693822450297748434301924950358561859804256788098033426537956252964976682327991427626735740
    Q_n = 20714298338160449749545360743688018842877274054540852096459485283936802341271363766157976112525034004319938054034934880860956966585051684483662535780621673316774842614701726445870630109196016676725183412879870463432277629916669130494040403733295593655306104176367902352484367520262917943100467697540593925707162162616635533550262718808746254599456286578409187895171015796991910123804529825519519278388910483133813330902530160448972926096083990208243274548561238253002789474920730760001104048093295680593033327818821255300893423412192265814418546134015557579236219461780344469127987669565138930308525189944897421753947
    Q_E_D = 100772079222298134586116156850742817855408127716962891929259868746672572602333918958075582671752493618259518286336122772703330183037221105058298653490794337885098499073583821832532798309513538383175233429533467348390389323225198805294950484802068148590902907221150968539067980432831310376368202773212266320112670699737501054831646286585142281419237572222713975646843555024731855688573834108711874406149540078253774349708158063055754932812675786123700768288048445326199880983717504538825498103789304873682191053050366806825802602658674268440844577955499368404019114913934477160428428662847012289516655310680119638600315228284298935201
    Ciphertext = 40855937355228438525361161524441274634175356845950884889338630813182607485910094677909779126550263304194796000904384775495000943424070396334435810126536165332565417336797036611773382728344687175253081047586602838685027428292621557914514629024324794275772522013126464926990620140406412999485728750385876868115091735425577555027394033416643032644774339644654011686716639760512353355719065795222201167219831780961308225780478482467294410828543488412258764446494815238766185728454416691898859462532083437213793104823759147317613637881419787581920745151430394526712790608442960106537539121880514269830696341737507717448946962021

    p, q = phi_n(P_n, P_F_n)
    P = nextprime(abs(2021 * p + 2020 * q))

    p, q = n_e_d(Q_n, Q_E_D)
    Q = nextprime(abs(2021 * p - 2020 * q))
    
    print(long_to_bytes(standard_rsa_decryption(e, Ciphertext, [P, Q])))

    # b'MRCTF{Ju3t_@_31mp13_que3t10n}'

4.32 [HDCTF2019]together

4.32.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# pubkey1.pem
-----BEGIN PUBLIC KEY-----
MIIBITANBgkqhkiG9w0BAQEFAAOCAQ4AMIIBCQKCAQB1qLiqKtKVDprtS+NGGN++
q7jLqDJoXMlPRRczMBAGJIRsz5Dzwtt1ulr0s5yu8RdaufiYeU6sYIKk92b3yygL
FvaYCzjdqBF2EyTWGVE7PL5lh3rPUfxwQFqDR8EhIH5x+Ob8rjlkftIjHTBt1ThJ
JXvDBumXpQKGcBIknRaR9dwR1q8GU58/gIk5ND3eCTAadhrhLByWkHbFArxalx4Q
q8s2ZUe8lDc/N6V93EOFjbKbqqqtDmhniF6jdXQDAIwWTpx6+jmzxlCJoVHd2MBs
ZCcQhvklWtuKz4IYL4+iUpMKGHlhY1vCqFx2EzD4XIljFLP9rk7+9+CoyTuIVL/D
AgMACR0=
-----END PUBLIC KEY-----


# pubkey2.pem
-----BEGIN PUBLIC KEY-----
MIIBIDANBgkqhkiG9w0BAQEFAAOCAQ0AMIIBCAKCAQB1qLiqKtKVDprtS+NGGN++
q7jLqDJoXMlPRRczMBAGJIRsz5Dzwtt1ulr0s5yu8RdaufiYeU6sYIKk92b3yygL
FvaYCzjdqBF2EyTWGVE7PL5lh3rPUfxwQFqDR8EhIH5x+Ob8rjlkftIjHTBt1ThJ
JXvDBumXpQKGcBIknRaR9dwR1q8GU58/gIk5ND3eCTAadhrhLByWkHbFArxalx4Q
q8s2ZUe8lDc/N6V93EOFjbKbqqqtDmhniF6jdXQDAIwWTpx6+jmzxlCJoVHd2MBs
ZCcQhvklWtuKz4IYL4+iUpMKGHlhY1vCqFx2EzD4XIljFLP9rk7+9+CoyTuIVL/D
AgJbJQ==
-----END PUBLIC KEY-----

# myflag1
R3Noy6r3WLItytAmb4FmHEygoilucEEZbO9ZYXx5JN03HNpBLDx7fXd2fl+UL5+11RCs/y0qlTGURWWDtG66eNLzGwNpAKiVj6I7RtUJl2Pcm3NvFeAFwI9UsVREyh7zIV6sI9ZP8l/2GVDorLAz5ULW+f0OINGhJmZm8FL/aDnlfTElhQ87LPicWpXYoMtyr6WrxjK6Ontn8BqCt0EjQ7TeXZhxIH9VTPWjDmFdmOqaqdVIT+LZemTgLNESwM5nn4g5S3aFDFwj1YiDYl0/+8etvKfOrfoKOwR0CxsRHagwdUUTES8EcHLmMGCxCkDZn3SzmmA6Nb3lgLeSgG8P1A==

# myflag2
O+rRCXI3aTB6P1rYIOPUdalUp6ujpwEq4I20CoWA+HIL8xxGtqY6N5gpr0guZv9ZgOEAMFnBxOqMdVNnB9GgnhmXtt1ZWydPqIcHvlfwpd/Lyd0XSjXnjaz3P3vOQvR71cD/uXyBA0XPzmnTIMgEhuGJVFm8min0L/2qI7wg/Z7w1+4mOmi655JIXeCiG23ukDv6l9bZuqfGvWCa1KKXWDP31nLbp0ZN2obUs6jEAa1qVTaX6M4My+sks+0VvHATrAUuCrmMwVEivqIJ/nS6ymGVERN6Ohnzyr168knEBKOVj0FAOx3YLfppMM+XbOGHeqdKJRLpMvqFXDMGQInT3w==

4.32.2 解题思路

提取公钥 + 共模攻击

4.32.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
import rsa
from base64 import b64decode
from Crypto.Util.number import long_to_bytes
import gmpy2

class ExtractKey:
    @staticmethod
    def extract_public_key(pem_str):
        """
        提取 PEM 格式公钥中的 n（模数）和 e（公钥指数）
        """
        pubkey = rsa.PublicKey.load_pkcs1_openssl_pem(pem_str.encode())
        return pubkey.n, pubkey.e

    @staticmethod
    def extract_private_key(pem_str):
        """
        提取 PEM 格式私钥中的 n（模数）和 d（私钥指数）
        """
        privkey = rsa.PrivateKey.load_pkcs1(pem_str.encode())
        return privkey.n, privkey.d


def common_modulus_attack(e1, e2, c1, c2, n):
    _, r, s = gmpy2.gcdext(e1, e2)
    m = pow(c1, r, n) * pow(c2, s, n) % n
    return m


if __name__ == '__main__':
    pubkey1 = '''
    -----BEGIN PUBLIC KEY-----
    MIIBITANBgkqhkiG9w0BAQEFAAOCAQ4AMIIBCQKCAQB1qLiqKtKVDprtS+NGGN++
    q7jLqDJoXMlPRRczMBAGJIRsz5Dzwtt1ulr0s5yu8RdaufiYeU6sYIKk92b3yygL
    FvaYCzjdqBF2EyTWGVE7PL5lh3rPUfxwQFqDR8EhIH5x+Ob8rjlkftIjHTBt1ThJ
    JXvDBumXpQKGcBIknRaR9dwR1q8GU58/gIk5ND3eCTAadhrhLByWkHbFArxalx4Q
    q8s2ZUe8lDc/N6V93EOFjbKbqqqtDmhniF6jdXQDAIwWTpx6+jmzxlCJoVHd2MBs
    ZCcQhvklWtuKz4IYL4+iUpMKGHlhY1vCqFx2EzD4XIljFLP9rk7+9+CoyTuIVL/D
    AgMACR0=
    -----END PUBLIC KEY-----
    '''

    pubkey2 = '''
    -----BEGIN PUBLIC KEY-----
    MIIBIDANBgkqhkiG9w0BAQEFAAOCAQ0AMIIBCAKCAQB1qLiqKtKVDprtS+NGGN++
    q7jLqDJoXMlPRRczMBAGJIRsz5Dzwtt1ulr0s5yu8RdaufiYeU6sYIKk92b3yygL
    FvaYCzjdqBF2EyTWGVE7PL5lh3rPUfxwQFqDR8EhIH5x+Ob8rjlkftIjHTBt1ThJ
    JXvDBumXpQKGcBIknRaR9dwR1q8GU58/gIk5ND3eCTAadhrhLByWkHbFArxalx4Q
    q8s2ZUe8lDc/N6V93EOFjbKbqqqtDmhniF6jdXQDAIwWTpx6+jmzxlCJoVHd2MBs
    ZCcQhvklWtuKz4IYL4+iUpMKGHlhY1vCqFx2EzD4XIljFLP9rk7+9+CoyTuIVL/D
    AgJbJQ==
    -----END PUBLIC KEY-----
    '''

    n, e1 = ExtractKey.extract_public_key(pubkey1)
    n, e2 = ExtractKey.extract_public_key(pubkey2)
    
    with open(r"myflag1","rb") as f:
        c1 = int.from_bytes(b64decode(f.read()))

    with open(r"myflag2","rb") as f:
        c2 = int.from_bytes(b64decode(f.read()))

    m = common_modulus_attack(e1, e2, c1, c2, n)
    print(long_to_bytes(m))

    # b'flag{23re_SDxF_y78hu_5rFgS}'

4.33 [INSHack2017]rsa16m

4.33.1 题目

1
2
3
4
5
# Challenge description:

When you need really secure communications, you use RSA with a 4096 bit key. <br>
I want really really really secure communications to transmit the nuclear launch codes (yeah IoT is everywhere man) so I used RSA with a 16777216 bit key. Surely russians will not be able to factor that one ! <br>
File md5 : 1049a0c83a2e34760363b4ad9778753f

附件： rsa_16m.zip

4.33.2 解题思路

RSA 低公钥指数攻击

4.33.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
import itertools
from gmpy2 import iroot
from Crypto.Util.number import long_to_bytes, GCD, inverse


def low_public_exponent_attack(n, c, e=None, lower=None, upper=None, phi=None):
    """
    RSA 低公钥指数攻击
    """
    if e is not None:
        # 小 e 且 m^e < n，可直接开 e 次方根
        for k in itertools.count():
            candidate = c + k * n
            root, exact = iroot(candidate, e)
            if exact:
                return int(root)
    elif phi is not None and lower is not None and upper is not None:
        # 若未知 e，则爆破 e，满足 gcd(e, φ) = 1 并计算 d
        for e_candidate in range(lower, upper):
            if GCD(e_candidate, phi) == 1:
                d = inverse(e_candidate, phi)
                m = pow(c, d, n)
                if b'flag' in long_to_bytes(m):
                    return m
    else:
        raise ValueError("参数不完整：请提供 e，或 (phi + low + high)")


if __name__ == "__main__":
    nec = {}
    with open(r"rsa_16m", 'r', encoding='utf-8') as f:
        for line in f:
            line = line.strip()  # 去除首尾空格和换行符
            if not line:
                continue  # 跳过空行
            # 分割键和值
            key, value = line.split('=', 1)
            key = key.strip()
            value = value.strip()
            # 转换为整数并存储
            if key in ['n', 'e', 'c']:
                nec[key] = int(value, 16)

    n = nec['n']
    e = nec['e']
    c = nec['c']
    print(long_to_bytes(low_public_exponent_attack(n, c, e)))

    # b'INSA{(I)NSA_W0uld_bE_pr0uD}'

4.34 坏蛋是雷宾

4.34.1 题目

1
老牌刺客之王混进了女王的住所。一天，女王得到了一个匿名举报，说她的侍卫里有一个刺客，叫做Rabin，而他的信息就在一份文件里，文件中有附带一个Pk，是523798549，密文是162853095，校验码二进制值是110001，根据说明是放在明文后一起加密的，明文与密文长度相同。加密算法和这位老牌刺客同名。快拯救女王，答案是求得的明文，进行32位md5小写哈希字符串，提交即可。

4.34.2 解题思路

RSA 低公钥指数攻击：特例 $ e=2 $ 的 Rabin 算法

奇偶校验

4.34.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
import hashlib
from typing import Union
from gmssl import sm3
from sympy import factorint
from Crypto.Util.number import isPrime, inverse

def hash_data(data: Union[bytes, str], algorithm: str, output_type: str = "hex", hash_length: int = None, hex_case: str = "lower") -> tuple:
    """
    计算数据的哈希值，支持多种算法和输出类型
    """
    # 统一转换为字节类型（兼容字符串输入）
    data_bytes = data.encode("utf-8") if isinstance(data, str) else data

    # 计算哈希值及长度
    match algorithm.lower():
        case "sha256" | "md5" | "sha1":
            hasher = hashlib.new(algorithm, data_bytes)
            digest = hasher.digest()
            original_length = hasher.digest_size

        case "sm3":
            hex_digest = sm3.sm3_hash(list(data_bytes))  # gmssl返回十六进制字符串
            digest = bytes.fromhex(hex_digest)           # 转换为字节
            original_length = 32                         # SM3固定32字节

        case _:
            raise ValueError(f"不支持的算法: {algorithm}（支持：sha256/md5/sha1/sm3）")

    # 长度控制
    if hash_length is not None:
        if not isinstance(hash_length, int) or hash_length <= 0:
            raise ValueError("hash_length必须是正整数")
        if hash_length > original_length:
            raise ValueError(f"长度超出限制（最大{original_length}字节）")
        digest = digest[:hash_length]  # 截断字节串
        actual_length = hash_length
    else:
        actual_length = original_length  # 不截断时使用原始长度

    # 转换输出类型
    match output_type.lower():
        case "bytes":
            result = digest
        case "hex":
            hex_str = digest.hex()
            # 十六进制大小写转换
            result = hex_str.upper() if hex_case.lower() == "upper" else hex_str.lower()
        case "int":
            result = int.from_bytes(digest, byteorder="big")
        case _:
            raise ValueError(f"不支持的输出类型: {output_type}（支持：bytes/hex/int）")

    return result, actual_length

class LowPublicExponentAttackRabin:
    def __init__(self, p=None, q=None):
        """
        初始化 Rabin 算法
        """
        if p and q:
            # 验证素数合法性（Rabin要求p ≡ 3 mod 4且q ≡ 3 mod 4）
            if not (isPrime(p) and isPrime(q) and p % 4 == 3 and q % 4 == 3):
                raise ValueError("p和q必须是形如4k+3的素数")
            self.p = p
            self.q = q
        else:
            # 自动生成符合条件的素数（简化版，实际应用需更大素数）
            self.p = self._generate_prime()
            self.q = self._generate_prime()
        
        self.n = self.p * self.q  # 公钥n = p*q

    def _generate_prime(self):
        """生成形如4k+3的素数（示例用小素数，实际需调整）"""
        candidate = 7  # 最小的4k+3素数是3，此处从7开始
        while True:
            if isPrime(candidate) and candidate % 4 == 3:
                return candidate
            candidate += 4  # 只检查4k+3形式的数

    def encrypt(self, plaintext):
        """加密：c = m² mod n"""
        if not isinstance(plaintext, int):
            raise TypeError("明文必须是整数")
        if plaintext < 0 or plaintext >= self.n:
            raise ValueError(f"明文必须在[0, {self.n})范围内")
        return pow(plaintext, 2, self.n)

    def decrypt(self, ciphertext):
        """解密：返回4个可能的明文"""
        if not isinstance(ciphertext, int):
            raise TypeError("密文必须是整数")
        
        # 计算模p和模q的平方根
        m_p1 = pow(ciphertext, (self.p + 1) // 4, self.p)
        m_p2 = (-m_p1) % self.p
        m_q1 = pow(ciphertext, (self.q + 1) // 4, self.q)
        m_q2 = (-m_q1) % self.q

        # 中国剩余定理合并结果
        inv_q_p = inverse(self.q, self.p)  # q在模p下的逆
        inv_p_q = inverse(self.p, self.q)  # p在模q下的逆

        m1 = (self.q * inv_q_p * m_p1 + self.p * inv_p_q * m_q1) % self.n
        m2 = (self.q * inv_q_p * m_p1 + self.p * inv_p_q * m_q2) % self.n
        m3 = (self.q * inv_q_p * m_p2 + self.p * inv_p_q * m_q1) % self.n
        m4 = (self.q * inv_q_p * m_p2 + self.p * inv_p_q * m_q2) % self.n

        return (m1, m2, m3, m4)

def parity_check(number, number_base=10, check_binary='0'):
    """
    判断 number 的二进制末尾6位是否等于 check_binary。
    """

    # 处理 number：统一转为整数
    if isinstance(number, str):
        num = int(number, base=number_base)
    elif isinstance(number, int):
        num = number
    else:
        raise ValueError("number 必须为 str 或 int")

    # 处理 check_binary：转为二进制字符串，保留前导零
    if isinstance(check_binary, str):
        check_str = check_binary.zfill(6)
    elif isinstance(check_binary, int):
        check_str = bin(check_binary)[2:].zfill(6)
    else:
        raise ValueError("check_binary 必须为 str 或 int")

    # 获取 number 的二进制末尾6位
    bin_last6 = bin(num)[-6:].zfill(6)

    return bin_last6 == check_str


if __name__ == "__main__":
    n = 523798549
    ct = 162853095
    check_code = 0b110001
    p, q = factorint(n)
    rabin = LowPublicExponentAttackRabin(p, q)
    pt = rabin.decrypt(ct)

    for num in pt:
        if parity_check(num, 10, 0b110001):
            plaintext = int(bin(num)[2:-6], 2)
            print(f'flag{{{hash_data(str(plaintext), "md5")[0]}}}')

            # flag{ca5cec442b2734735406d78c88e90f35}

4.35 [INSHack2019]Yet Another RSA Challenge - Part 1

4.35.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
import subprocess
p = subprocess.check_output('openssl prime -generate -bits 2048 -hex')
q = subprocess.check_output('openssl prime -generate -bits 2048 -hex')
flag = int('INSA{REDACTED}'.encode('hex'), 16)

N = int(p,16) * int(q,16)
print N
print '0x'+p.replace('9F','FC')
print pow(flag,65537,N)

719579745653303119025873098043848913976880838286635817351790189702008424828505522253331968992725441130409959387942238566082746772468987336980704680915524591881919460709921709513741059003955050088052599067720107149755856317364317707629467090624585752920523062378696431510814381603360130752588995217840721808871896469275562085215852034302374902524921137398710508865248881286824902780186249148613287250056380811479959269915786545911048030947364841177976623684660771594747297272818410589981294227084173316280447729440036251406684111603371364957690353449585185893322538541593242187738587675489180722498945337715511212885934126635221601469699184812336984707723198731876940991485904637481371763302337637617744175461566445514603405016576604569057507997291470369704260553992902776099599438704680775883984720946337235834374667842758010444010254965664863296455406931885650448386682827401907759661117637294838753325610213809162253020362015045242003388829769019579522792182295457962911430276020610658073659629786668639126004851910536565721128484604554703970965744790413684836096724064390486888113608024265771815004188203124405817878645103282802994701531113849607969243815078720289912255827700390198089699808626116357304202660642601149742427766381
0xDCC5A0BD3A1FC0BEB0DA1C2E8CF6B474481B7C12849B76E03C4C946724DB577D2825D6AA193DB559BC9DBABE1DDE8B5E7805E48749EF002F622F7CDBD7853B200E2A027E87E331AFCFD066ED9900F1E5F5E5196A451A6F9E329EB889D773F08E5FBF45AACB818FD186DD74626180294DCC31805A88D1B71DE5BFEF3ED01F12678D906A833A78EDCE9BDAF22BBE45C0BFB7A82AFE42C1C3B8581C83BF43DFE31BFD81527E507686956458905CC9A660604552A060109DC81D01F229A264AB67C6D7168721AB36DE769CEAFB97F238050193EC942078DDF5329A387F46253A4411A9C8BB71F9AEB11AC9623E41C14FCD2739D76E69283E57DDB11FC531B4611EE3
596380963583874022971492302071822444225514552231574984926542429117396590795270181084030717066220888052607057994262255729890598322976783889090993129161030148064314476199052180347747135088933481343974996843632511300255010825580875930722684714290535684951679115573751200980708359500292172387447570080875531002842462002727646367063816531958020271149645805755077133231395881833164790825731218786554806777097126212126561056170733032553159740167058242065879953688453169613384659653035659118823444582576657499974059388261153064772228570460351169216103620379299362366574826080703907036316546232196313193923841110510170689800892941998845140534954264505413254429240789223724066502818922164419890197058252325607667959185100118251170368909192832882776642565026481260424714348087206462283972676596101498123547647078981435969530082351104111747783346230914935599764345176602456069568419879060577771404946743580809330315332836749661503035076868102720709045692483171306425207758972682717326821412843569770615848397477633761506670219845039890098105484693890695897858251238713238301401843678654564558196040100908796513657968507381392735855990706254646471937809011610992016368630851454275478216664521360246605400986428230407975530880206404171034278692756

4.35.2 解题思路

$ p $ 参数泄露（注意：有的 FC 不需要替换，需要爆破所有可能）

4.35.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
from math import prod
from sympy import totient
from base64 import b64decode
from itertools import product
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
from Crypto.Util.number import inverse, long_to_bytes


def standard_rsa_decryption(e, c, primes=None, n=None, phi=None, ct_format='int'):
    """
    标准 RSA 解密
    """
    if not phi:
        if n:
            phi = totient(n)
        else:
            phi = prod(p - 1 for p in primes)
            n = prod(p for p in primes)

    d = inverse(e, phi)
    
    if ct_format == 'base64':
        p, q = primes[0], primes[1]
        key_info = RSA.construct((n, e, d, p, q))
        key = RSA.importKey(key_info.exportKey())
        key = PKCS1_OAEP.new(key)
        m = key.decrypt(b64decode(c)).decode()
    else:
        m = pow(c, d, n)

    return m


if __name__ == "__main__":
    e = 65537
    n = 719579745653303119025873098043848913976880838286635817351790189702008424828505522253331968992725441130409959387942238566082746772468987336980704680915524591881919460709921709513741059003955050088052599067720107149755856317364317707629467090624585752920523062378696431510814381603360130752588995217840721808871896469275562085215852034302374902524921137398710508865248881286824902780186249148613287250056380811479959269915786545911048030947364841177976623684660771594747297272818410589981294227084173316280447729440036251406684111603371364957690353449585185893322538541593242187738587675489180722498945337715511212885934126635221601469699184812336984707723198731876940991485904637481371763302337637617744175461566445514603405016576604569057507997291470369704260553992902776099599438704680775883984720946337235834374667842758010444010254965664863296455406931885650448386682827401907759661117637294838753325610213809162253020362015045242003388829769019579522792182295457962911430276020610658073659629786668639126004851910536565721128484604554703970965744790413684836096724064390486888113608024265771815004188203124405817878645103282802994701531113849607969243815078720289912255827700390198089699808626116357304202660642601149742427766381
    p_leak = 0xDCC5A0BD3A1FC0BEB0DA1C2E8CF6B474481B7C12849B76E03C4C946724DB577D2825D6AA193DB559BC9DBABE1DDE8B5E7805E48749EF002F622F7CDBD7853B200E2A027E87E331AFCFD066ED9900F1E5F5E5196A451A6F9E329EB889D773F08E5FBF45AACB818FD186DD74626180294DCC31805A88D1B71DE5BFEF3ED01F12678D906A833A78EDCE9BDAF22BBE45C0BFB7A82AFE42C1C3B8581C83BF43DFE31BFD81527E507686956458905CC9A660604552A060109DC81D01F229A264AB67C6D7168721AB36DE769CEAFB97F238050193EC942078DDF5329A387F46253A4411A9C8BB71F9AEB11AC9623E41C14FCD2739D76E69283E57DDB11FC531B4611EE3
    c = 596380963583874022971492302071822444225514552231574984926542429117396590795270181084030717066220888052607057994262255729890598322976783889090993129161030148064314476199052180347747135088933481343974996843632511300255010825580875930722684714290535684951679115573751200980708359500292172387447570080875531002842462002727646367063816531958020271149645805755077133231395881833164790825731218786554806777097126212126561056170733032553159740167058242065879953688453169613384659653035659118823444582576657499974059388261153064772228570460351169216103620379299362366574826080703907036316546232196313193923841110510170689800892941998845140534954264505413254429240789223724066502818922164419890197058252325607667959185100118251170368909192832882776642565026481260424714348087206462283972676596101498123547647078981435969530082351104111747783346230914935599764345176602456069568419879060577771404946743580809330315332836749661503035076868102720709045692483171306425207758972682717326821412843569770615848397477633761506670219845039890098105484693890695897858251238713238301401843678654564558196040100908796513657968507381392735855990706254646471937809011610992016368630851454275478216664521360246605400986428230407975530880206404171034278692756

    # 生成所有可能的替换组合
    hex_str = hex(p_leak)[2:].upper()
    fc_indices = [i for i in range(len(hex_str)-1) if hex_str[i:i+2] == 'FC']

    for replace_mask in product([False, True], repeat=len(fc_indices)):
        # 根据替换掩码生成新的十六进制
        chars = list(hex_str)
        for do_replace, idx in zip(replace_mask, fc_indices):
            if do_replace:
                chars[idx:idx+2] = ['9', 'F']
        
        p = int(''.join(chars), 16)
        if n % p == 0:
            q = n // p
            print(long_to_bytes(standard_rsa_decryption(e, c, [p, q])))

            # b'INSA{I_w1ll_us3_OTp_n3xT_T1M3}'

4.36 [RoarCTF2019]RSA

4.36.1 题目

1
2
3
4
5
6
A=(((y%x)**5)%(x%y))**2019+y**316+(y+1)/x
p=next_prime(z*x*y)
q=next_prime(z)
A =  2683349182678714524247469512793476009861014781004924905484127480308161377768192868061561886577048646432382128960881487463427414176114486885830693959404989743229103516924432512724195654425703453612710310587164417035878308390676612592848750287387318129424195208623440294647817367740878211949147526287091298307480502897462279102572556822231669438279317474828479089719046386411971105448723910594710418093977044179949800373224354729179833393219827789389078869290217569511230868967647963089430594258815146362187250855166897553056073744582946148472068334167445499314471518357535261186318756327890016183228412253724
n =  117930806043507374325982291823027285148807239117987369609583515353889814856088099671454394340816761242974462268435911765045576377767711593100416932019831889059333166946263184861287975722954992219766493089630810876984781113645362450398009234556085330943125568377741065242183073882558834603430862598066786475299918395341014877416901185392905676043795425126968745185649565106322336954427505104906770493155723995382318346714944184577894150229037758434597242564815299174950147754426950251419204917376517360505024549691723683358170823416757973059354784142601436519500811159036795034676360028928301979780528294114933347127
c =  41971850275428383625653350824107291609587853887037624239544762751558838294718672159979929266922528917912189124713273673948051464226519605803745171340724343705832198554680196798623263806617998072496026019940476324971696928551159371970207365741517064295956376809297272541800647747885170905737868568000101029143923792003486793278197051326716680212726111099439262589341050943913401067673851885114314709706016622157285023272496793595281054074260451116213815934843317894898883215362289599366101018081513215120728297131352439066930452281829446586562062242527329672575620261776042653626411730955819001674118193293313612128

4.36.2 解题思路

$ A $ 长度为 $ 2015 \lt 2019 $，所以 $ \left( (y \bmod x)^5 \bmod (x \bmod y) \right)^{2019} $ 值只能为 1 或 0，并且 $ \frac{y+1}{x} $ 结果要求为整数。$A$ 近似 $ y^{316} $，可解 $ x $ 和 $ y $。

p、q 参数设置不当（近似攻击）

4.36.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from Crypto.Util.number import inverse, long_to_bytes, isPrime
from gmpy2 import iroot


def p_q_approximation(n, n1, e, c):
    p = iroot(n1, 2)[0]
    while n % p != 0 :
        p += 1
    
    q = n // p
    d = inverse(e, (p-1)*(q-1))
    return pow(c, d, n)


if __name__ == '__main__':
    e = 65537
    A = 2683349182678714524247469512793476009861014781004924905484127480308161377768192868061561886577048646432382128960881487463427414176114486885830693959404989743229103516924432512724195654425703453612710310587164417035878308390676612592848750287387318129424195208623440294647817367740878211949147526287091298307480502897462279102572556822231669438279317474828479089719046386411971105448723910594710418093977044179949800373224354729179833393219827789389078869290217569511230868967647963089430594258815146362187250855166897553056073744582946148472068334167445499314471518357535261186318756327890016183228412253724
    n = 117930806043507374325982291823027285148807239117987369609583515353889814856088099671454394340816761242974462268435911765045576377767711593100416932019831889059333166946263184861287975722954992219766493089630810876984781113645362450398009234556085330943125568377741065242183073882558834603430862598066786475299918395341014877416901185392905676043795425126968745185649565106322336954427505104906770493155723995382318346714944184577894150229037758434597242564815299174950147754426950251419204917376517360505024549691723683358170823416757973059354784142601436519500811159036795034676360028928301979780528294114933347127
    c = 41971850275428383625653350824107291609587853887037624239544762751558838294718672159979929266922528917912189124713273673948051464226519605803745171340724343705832198554680196798623263806617998072496026019940476324971696928551159371970207365741517064295956376809297272541800647747885170905737868568000101029143923792003486793278197051326716680212726111099439262589341050943913401067673851885114314709706016622157285023272496793595281054074260451116213815934843317894898883215362289599366101018081513215120728297131352439066930452281829446586562062242527329672575620261776042653626411730955819001674118193293313612128

    y = iroot(A, 316)[0]
    if (y+1) % ((A-1) - y**316) == 0:
        x = (y+1) // ((A-1) - y**316)
    else:
        x = (y+1) // (A - y**316)
    
    m = p_q_approximation(n, n // x // y, e, c)
    print(long_to_bytes(m))

    # b'RoarCTF{wm-l1l1ll1l1l1l111ll}'

5. 哈希与消息认证

5.1 MD5

5.1.1 题目

1
e00cf25ad42683b3df678c61f42c6bda

5.1.2 解题思路

MD5 在线查询

5.1.3 解题脚本

1
2
3
https://www.cmd5.com/default.aspx

# flag{admin1}

5.2 丢失的MD5

5.2.1 题目

1
2
3
4
5
6
7
8
9
import hashlib   
for i in range(32,127):
    for j in range(32,127):
        for k in range(32,127):
            m=hashlib.md5()
            m.update('TASC'+chr(i)+'O3RJMV'+chr(j)+'WDJKX'+chr(k)+'ZM')
            des=m.hexdigest()
            if 'e9032' in des and 'da' in des and '911513' in des:
                print des

5.2.2 解题思路

MD5 爆破

针对特定 MD5 哈希值的爆破。遍历 ASCII 字符（32-126）寻找符合特定子串条件的 MD5 哈希值。

5.2.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
import hashlib
from typing import Union
from gmssl import sm3

def hash_data(data: Union[bytes, str], algorithm: str, output_type: str = "hex", hash_length: int = None, hex_case: str = "lower") -> tuple:
    """
    计算数据的哈希值，支持多种算法和输出类型
    """
    # 统一转换为字节类型（兼容字符串输入）
    data_bytes = data.encode("utf-8") if isinstance(data, str) else data

    # 计算哈希值及长度
    match algorithm.lower():
        case "sha256" | "md5" | "sha1":
            hasher = hashlib.new(algorithm, data_bytes)
            digest = hasher.digest()
            original_length = hasher.digest_size

        case "sm3":
            hex_digest = sm3.sm3_hash(list(data_bytes))  # gmssl返回十六进制字符串
            digest = bytes.fromhex(hex_digest)           # 转换为字节
            original_length = 32                         # SM3固定32字节

        case _:
            raise ValueError(f"不支持的算法: {algorithm}（支持：sha256/md5/sha1/sm3）")

    # 长度控制
    if hash_length is not None:
        if not isinstance(hash_length, int) or hash_length <= 0:
            raise ValueError("hash_length必须是正整数")
        if hash_length > original_length:
            raise ValueError(f"长度超出限制（最大{original_length}字节）")
        digest = digest[:hash_length]  # 截断字节串
        actual_length = hash_length
    else:
        actual_length = original_length  # 不截断时使用原始长度

    # 转换输出类型
    match output_type.lower():
        case "bytes":
            result = digest
        case "hex":
            hex_str = digest.hex()
            # 十六进制大小写转换
            result = hex_str.upper() if hex_case.lower() == "upper" else hex_str.lower()
        case "int":
            result = int.from_bytes(digest, byteorder="big")
        case _:
            raise ValueError(f"不支持的输出类型: {output_type}（支持：bytes/hex/int）")

    return result, actual_length


if __name__ == '__main__':
    for i in range(32,127):
        for j in range(32,127):
            for k in range(32,127):
                m = 'TASC'+chr(i)+'O3RJMV'+chr(j)+'WDJKX'+chr(k)+'ZM'
                des, _ = hash_data(m, 'md5')
                if 'e9032' in des and 'da' in des and '911513' in des:
                    print(f'flag{{{m}}}')
    
                    # flag{TASCJO3RJMVKWDJKXLZM}

5.3 Windows系统密码

5.3.1 题目

1
2
3
4
Administrator:500:aad3b435b51404eeaad3b435b51404ee:31d6cfe0d16ae931b73c59d7e0c089c0:::
ctf:1002:06af9108f2e1fecf144e2e8adef09efd:a7fcb22a88038f35a8f39d503e7f0062:::
Guest:501:aad3b435b51404eeaad3b435b51404ee:31d6cfe0d16ae931b73c59d7e0c089c0:::
SUPPORT_388945a0:1001:aad3b435b51404eeaad3b435b51404ee:bef14eee40dffbc345eeb3f58e290d56:::

5.3.2 解题思路

MD5 在线查询

5.3.3 解题脚本

1
2
3
https://www.cmd5.com/default.aspx

# flag{good-luck}

5.4 权限获得第一步

5.4.1 题目

1
Administrator:500:806EDC27AA52E314AAD3B435B51404EE:F4AD50F57683D4260DFD48AA351A17A8:::

5.4.2 解题思路

MD5 在线查询

5.4.3 解题脚本

1
2
3
4
https://www.cmd5.com/default.aspx

# F4AD50F57683D4260DFD48AA351A17A8 -> 3617656
flag{3617656}

5.5 还原大师

5.5.1 题目

1
我们得到了一串神秘字符串：TASC?O3RJMV?WDJKX?ZM,问号部分是未知大写字母，为了确定这个神秘字符串，我们通过了其他途径获得了这个字串的32位MD5码。但是我们获得它的32位MD5码也是残缺不全，E903???4DAB????08?????51?80??8A?,请猜出神秘字符串的原本模样，并且提交这个字串的32位MD5码作为答案。

5.5.2 解题思路

MD5 爆破

针对特定 MD5 哈希值的爆破。遍历 ASCII 字符（32-126）寻找符合特定子串条件的 MD5 哈希值。

5.5.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
import hashlib
from typing import Union
from gmssl import sm3

def hash_data(data: Union[bytes, str], algorithm: str, output_type: str = "hex", hash_length: int = None, hex_case: str = "lower") -> tuple:
    """
    计算数据的哈希值，支持多种算法和输出类型
    """
    # 统一转换为字节类型（兼容字符串输入）
    data_bytes = data.encode("utf-8") if isinstance(data, str) else data

    # 计算哈希值及长度
    match algorithm.lower():
        case "sha256" | "md5" | "sha1":
            hasher = hashlib.new(algorithm, data_bytes)
            digest = hasher.digest()
            original_length = hasher.digest_size

        case "sm3":
            hex_digest = sm3.sm3_hash(list(data_bytes))  # gmssl返回十六进制字符串
            digest = bytes.fromhex(hex_digest)           # 转换为字节
            original_length = 32                         # SM3固定32字节

        case _:
            raise ValueError(f"不支持的算法: {algorithm}（支持：sha256/md5/sha1/sm3）")

    # 长度控制
    if hash_length is not None:
        if not isinstance(hash_length, int) or hash_length <= 0:
            raise ValueError("hash_length必须是正整数")
        if hash_length > original_length:
            raise ValueError(f"长度超出限制（最大{original_length}字节）")
        digest = digest[:hash_length]  # 截断字节串
        actual_length = hash_length
    else:
        actual_length = original_length  # 不截断时使用原始长度

    # 转换输出类型
    match output_type.lower():
        case "bytes":
            result = digest
        case "hex":
            hex_str = digest.hex()
            # 十六进制大小写转换
            result = hex_str.upper() if hex_case.lower() == "upper" else hex_str.lower()
        case "int":
            result = int.from_bytes(digest, byteorder="big")
        case _:
            raise ValueError(f"不支持的输出类型: {output_type}（支持：bytes/hex/int）")

    return result, actual_length


if __name__ == '__main__':
    for i in range(32,127):
        for j in range(32,127):
            for k in range(32,127):
                m = 'TASC'+chr(i)+'O3RJMV'+chr(j)+'WDJKX'+chr(k)+'ZM'
                des, _ = hash_data(m, 'md5')
                if 'e9032' in des and 'da' in des and '911513' in des:
                    print(f'flag{{{des.upper()}}}')
    
                    # flag{e9032994dabac08080091151380478a2}

6. 应用密码学


7. 自定义构造题

7.1 Alice与Bob

7.1.1 题目

1
密码学历史中，有两位知名的杰出人物，Alice和Bob。他们的爱情经过置换和轮加密也难以混淆，即使是没有身份认证也可以知根知底。就像在数学王国中的素数一样，孤傲又热情。下面是一个大整数:98554799767,请分解为两个素数，分解后，小的放前面，大的放后面，合成一个新的数字，进行md5的32位小写哈希，提交答案。

7.1.2 解题思路

按照题目步骤写脚本。

7.1.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
import requests
import hashlib
from gmssl import sm3
from typing import Optional, Union

def queryFactors(n):
    """查询整数n的质因数分解结果"""
    response = requests.get(f"http://factordb.com/api?query={n}")
    return [int(factor) for factor, count in response.json()["factors"] for _ in range(int(count))]


def hash_data(data: Union[bytes, str], algorithm: str, output_type: str = "hex", hash_length: int = None, hex_case: str = "lower") -> tuple:
    """
    计算数据的哈希值，支持多种算法和输出类型
    """
    # 统一转换为字节类型（兼容字符串输入）
    data_bytes = data.encode("utf-8") if isinstance(data, str) else data

    # 计算哈希值及长度
    match algorithm.lower():
        case "sha256" | "md5" | "sha1":
            hasher = hashlib.new(algorithm, data_bytes)
            digest = hasher.digest()
            original_length = hasher.digest_size

        case "sm3":
            hex_digest = sm3.sm3_hash(list(data_bytes))  # gmssl返回十六进制字符串
            digest = bytes.fromhex(hex_digest)           # 转换为字节
            original_length = 32                             # SM3固定32字节

        case _:
            raise ValueError(f"不支持的算法: {algorithm}（支持：sha256/md5/sha1/sm3）")

    # 长度控制
    if hash_length is not None:
        if not isinstance(hash_length, int) or hash_length <= 0:
            raise ValueError("hash_length必须是正整数")
        if hash_length > original_length:
            raise ValueError(f"长度超出限制（最大{original_length}字节）")
        digest = digest[:hash_length]  # 截断字节串
        actual_length = hash_length
    else:
        actual_length = original_length  # 不截断时使用原始长度

    # 转换输出类型
    match output_type.lower():
        case "bytes":
            result = digest
        case "hex":
            hex_str = digest.hex()
            # 十六进制大小写转换
            result = hex_str.upper() if hex_case.lower() == "upper" else hex_str.lower()
        case "int":
            result = int.from_bytes(digest, byteorder="big")
        case _:
            raise ValueError(f"不支持的输出类型: {output_type}（支持：bytes/hex/int）")

    return result, actual_length


if __name__ == '__main__':
    n=98554799767
    p = sorted(queryFactors(n))
    print(f"flag{{{hash_data(str(p[0]) + str(p[1]), 'md5', hash_length=16)[0]}}}")

    # flag{d450209323a847c8d01c6be47c81811a}

7.2 达芬奇密码

7.2.1 题目

1
2
3
4
达芬奇一直是一个有争议的画家，科学家。。。小明为了研究他，从网上找到了名画蒙娜丽莎，一天深夜，小明突然从蒙娜丽莎背后的天空中看到了一串神秘的数字。顺带告诉小明达芬奇家窗台上有一串数字是关键。小明千里迢迢找到了这串数字，请将这个送分题做出来，亲，包邮哦（答案是一串32位十进制数字） 

达芬奇隐藏在蒙娜丽莎中的数字列:1 233 3 2584 1346269 144 5 196418 21 1597 610 377 10946 89 514229 987 8 55 6765 2178309 121393 317811 46368 4181 1 832040 2 28657 75025 34 13 17711 
记录在达芬奇窗台口的神秘数字串:36968853882116725547342176952286

7.2.2 解题思路

斐波拉契数列

数字列与数字串长度相同。依次取出数字列中的每个数字，查找其在斐波那契数列中的索引值，然后将密文中对应索引位置的字符移动到该索引指定的新位置，实现还原。

7.2.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from collections import deque

def fibonacci(length: int) -> list:
    """生成指定长度的斐波那契数列"""
    sequence = [0, 1][:max(0, length)]
    for _ in range(2, length):
        sequence.append(sequence[-1] + sequence[-2])
    return sequence[1:]

if __name__ == '__main__':
    ct = deque("36968853882116725547342176952286")
    hint = [1, 233, 3, 2584, 1346269, 144, 5, 196418, 21, 1597, 610, 377, 10946, 89, 514229, 987, 8, 55, 6765, 2178309, 121393, 317811, 46368, 4181, 1, 832040, 2, 28657, 75025, 34, 13, 17711]
    fb = fibonacci(50)
    flag = ["*"] * len(ct)

    for i in hint:
        flag[fb.index(i)] = ct.popleft()
        fb[fb.index(i)] = '*'

    print(f"flag{{{''.join(flag)}}}")

    # flag{37995588256861228614165223347687}

7.3 [BJDCTF2020]easyrsa

7.3.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from Crypto.Util.number import getPrime,bytes_to_long
from sympy import Derivative
from fractions import Fraction
from secret import flag

p=getPrime(1024)
q=getPrime(1024)
e=65537
n=p*q
z=Fraction(1,Derivative(arctan(p),p))-Fraction(1,Derivative(arth(q),q))
m=bytes_to_long(flag)
c=pow(m,e,n)
print(c,z,n)
'''
output:
7922547866857761459807491502654216283012776177789511549350672958101810281348402284098310147796549430689253803510994877420135537268549410652654479620858691324110367182025648788407041599943091386227543182157746202947099572389676084392706406084307657000104665696654409155006313203957292885743791715198781974205578654792123191584957665293208390453748369182333152809882312453359706147808198922916762773721726681588977103877454119043744889164529383188077499194932909643918696646876907327364751380953182517883134591810800848971719184808713694342985458103006676013451912221080252735948993692674899399826084848622145815461035
32115748677623209667471622872185275070257924766015020072805267359839059393284316595882933372289732127274076434587519333300142473010344694803885168557548801202495933226215437763329280242113556524498457559562872900811602056944423967403777623306961880757613246328729616643032628964072931272085866928045973799374711846825157781056965164178505232524245809179235607571567174228822561697888645968559343608375331988097157145264357626738141646556353500994924115875748198318036296898604097000938272195903056733565880150540275369239637793975923329598716003350308259321436752579291000355560431542229699759955141152914708362494482
15310745161336895413406690009324766200789179248896951942047235448901612351128459309145825547569298479821101249094161867207686537607047447968708758990950136380924747359052570549594098569970632854351825950729752563502284849263730127586382522703959893392329333760927637353052250274195821469023401443841395096410231843592101426591882573405934188675124326997277775238287928403743324297705151732524641213516306585297722190780088180705070359469719869343939106529204798285957516860774384001892777525916167743272419958572055332232056095979448155082465977781482598371994798871917514767508394730447974770329967681767625495394441

'''

7.3.2 解题思路

三角函数

化简：$ \frac{1}{\frac{d}{dp} \arctan(p)} - \frac{1}{\frac{d}{dq} \operatorname{arth}(q)} $

对于 $\arctan(p)$，求导函数得：$\frac{d}{dp} \arctan(p)=\frac{1}{1+p^2}$；对于 $\operatorname{arth}(q)$（即 $\tanh^{-1}(q)$），求导函数得：$ \frac{d}{dp} \operatorname{arth}(q)=\frac{1}{1-q^2} $。可得：$ z=p^2+q^2 $。

已知 $p^2+q^2$ 和 $p \cdot q$ 可求 $ p 、 q $。

7.3.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import math
from Crypto.Util.number import inverse, long_to_bytes


def p_q_e_c(p, q, e, c):
    N = p*q
    d = inverse(e, (p-1)*(q-1))
    m = pow(c, d, N)
    return long_to_bytes(m)

if __name__ == "__main__":
    e = 65537
    c = 7922547866857761459807491502654216283012776177789511549350672958101810281348402284098310147796549430689253803510994877420135537268549410652654479620858691324110367182025648788407041599943091386227543182157746202947099572389676084392706406084307657000104665696654409155006313203957292885743791715198781974205578654792123191584957665293208390453748369182333152809882312453359706147808198922916762773721726681588977103877454119043744889164529383188077499194932909643918696646876907327364751380953182517883134591810800848971719184808713694342985458103006676013451912221080252735948993692674899399826084848622145815461035
    z = 32115748677623209667471622872185275070257924766015020072805267359839059393284316595882933372289732127274076434587519333300142473010344694803885168557548801202495933226215437763329280242113556524498457559562872900811602056944423967403777623306961880757613246328729616643032628964072931272085866928045973799374711846825157781056965164178505232524245809179235607571567174228822561697888645968559343608375331988097157145264357626738141646556353500994924115875748198318036296898604097000938272195903056733565880150540275369239637793975923329598716003350308259321436752579291000355560431542229699759955141152914708362494482
    n = 15310745161336895413406690009324766200789179248896951942047235448901612351128459309145825547569298479821101249094161867207686537607047447968708758990950136380924747359052570549594098569970632854351825950729752563502284849263730127586382522703959893392329333760927637353052250274195821469023401443841395096410231843592101426591882573405934188675124326997277775238287928403743324297705151732524641213516306585297722190780088180705070359469719869343939106529204798285957516860774384001892777525916167743272419958572055332232056095979448155082465977781482598371994798871917514767508394730447974770329967681767625495394441

    # 计算 p+q
    s = math.isqrt(z + 2 * n)
    
    # 解二次方程 x² - sx + m = 0
    discriminant = s * s - 4 * n
    sqrt_d = math.isqrt(discriminant)
    p = (s + sqrt_d) // 2
    q = (s - sqrt_d) // 2
    print(p_q_e_c(p, q, e, c))

    # b'BJD{Advanced_mathematics_is_too_hard!!!}'

7.4 [网鼎杯 2020 青龙组]boom

7.4.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
int __cdecl main(int argc, const char **argv, const char **envp)
{
  size_t v3; // eax
  char Str[50]; // [esp+24h] [ebp-128h] BYREF
  unsigned __int8 v6[50]; // [esp+56h] [ebp-F6h] BYREF
  _DWORD v7[16]; // [esp+88h] [ebp-C4h]
  unsigned int v8[22]; // [esp+C8h] [ebp-84h] BYREF
  __int64 v9; // [esp+120h] [ebp-2Ch] BYREF
  int v10; // [esp+12Ch] [ebp-20h] BYREF
  int v11; // [esp+130h] [ebp-1Ch] BYREF
  int v12; // [esp+134h] [ebp-18h] BYREF
  int v13; // [esp+138h] [ebp-14h]
  int i; // [esp+13Ch] [ebp-10h]

  __main();
  menu();
  system("pause");
  system("cls");
  v7[0] = 70;
  v7[1] = 229;
  v7[2] = 239;
  v7[3] = 230;
  v7[4] = 22;
  v7[5] = 90;
  v7[6] = 90;
  v7[7] = 251;
  v7[8] = 54;
  v7[9] = 18;
  v7[10] = 23;
  v7[11] = 68;
  v7[12] = 106;
  v7[13] = 45;
  v7[14] = 189;
  v7[15] = 1;
  puts("first:this string md5:46e5efe6165a5afb361217446a2dbd01");
  scanf("%s", Str);
  MD5Init(v8);
  v3 = strlen(Str);
  MD5Update((int)v8, Str, v3);
  MD5Final(v8, v6);
  v13 = 1;
  for ( i = 0; i <= 15; ++i )
  {
    if ( v6[i] != v7[i] )
    {
      v13 = 0;
      break;
    }
  }
  if ( v13 != 1 )
  {
    printf("Game over");
    system("pause");
    exit(0);
  }
  puts("Great next level");
  system("pause");
  system("cls");
  puts("This time:Here are have some formulas");
  puts("3x-y+z=185");
  puts("2x+3y-z=321");
  puts("x+y+z=173");
  printf("input: x = ");
  scanf("%d", &v12);
  printf("input: y = ");
  scanf("%d", &v11);
  printf("input : z = ");
  scanf("%d", &v10);
  if ( 3 * v12 - v11 + v10 != 185 || 2 * v12 + 3 * v11 - v10 != 321 || v11 + v12 + v10 != 173 )
  {
    printf("Game over");
    exit(0);
  }
  printf("Great last level coming...");
  printf("pause");
  system("cls");
  puts("Last time: Kill it");
  puts("x*x+x-7943722218936282=0");
  printf("input x: ");
  scanf("%lld", &v9);
  if ( v9 * (v9 + 1) != 0x1C38C5F50DD7DALL )
  {
    printf("Game over");
    exit(0);
  }
  puts("Great This is your FLAG");
  printf("flag{%s_%d%d%d_%lld}", Str, v12, v11, v10, v9);
  return 0;
}

7.4.2 解题思路

使用 IDA 反汇编 boom.exe，分析代码，flag 由三部分组成。

MD5 爆破 + 解三元一次方程组 + 解一元二次方程

7.4.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# https://www.cmd5.com/default.aspx
# 46e5efe6165a5afb361217446a2dbd01 -> en5oy

from sympy import symbols, solve, Eq


if __name__ == "__main__":
    # 定义未知数
    x, y, z = symbols('x y z')

    # 定义方程组
    equations = [
        Eq(x + y + z, 173),
        Eq(2*x + 3*y - z, 321),
        Eq(3*x - y + z, 185)
    ]
    sol1 = solve(equations, (x, y, z), dict=True)
    print(sol1)

    a = symbols('a')

    # 定义方程：x² + x - 7943722218936282 = 0
    equation = Eq(a**2 + a - 7943722218936282, 0)
    sol2 = solve(equation, a)
    print(sol2)
    
    print('flag{' + f'en5oy_{sol1[0][x]}{sol1[0][y]}{sol1[0][z]}_{sol2[1]}' + '}')

    # flag{en5oy_746831_89127561}

7.5 [RoarCTF2019]babyRSA

7.5.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import sympy
import random

def myGetPrime():
    A= getPrime(513)
    print(A)
    B=A-random.randint(1e3,1e5)
    print(B)
    return sympy.nextPrime((B!)%A)
p=myGetPrime()
#A1=21856963452461630437348278434191434000066076750419027493852463513469865262064340836613831066602300959772632397773487317560339056658299954464169264467234407
#B1=21856963452461630437348278434191434000066076750419027493852463513469865262064340836613831066602300959772632397773487317560339056658299954464169264467140596

q=myGetPrime()
#A2=16466113115839228119767887899308820025749260933863446888224167169857612178664139545726340867406790754560227516013796269941438076818194617030304851858418927
#B2=16466113115839228119767887899308820025749260933863446888224167169857612178664139545726340867406790754560227516013796269941438076818194617030304851858351026

r=myGetPrime()

n=p*q*r
#n=85492663786275292159831603391083876175149354309327673008716627650718160585639723100793347534649628330416631255660901307533909900431413447524262332232659153047067908693481947121069070451562822417357656432171870951184673132554213690123308042697361969986360375060954702920656364144154145812838558365334172935931441424096270206140691814662318562696925767991937369782627908408239087358033165410020690152067715711112732252038588432896758405898709010342467882264362733
c=pow(flag,e,n)
#e=0x1001
#c=75700883021669577739329316795450706204502635802310731477156998834710820770245219468703245302009998932067080383977560299708060476222089630209972629755965140317526034680452483360917378812244365884527186056341888615564335560765053550155758362271622330017433403027261127561225585912484777829588501213961110690451987625502701331485141639684356427316905122995759825241133872734362716041819819948645662803292418802204430874521342108413623635150475963121220095236776428
#so,what is the flag?

7.5.2 解题思路

威尔逊定理：$ (A-1)! \equiv -1 \pmod A $

分析代码：$p = (B_1!) % A_1 \quad q = (B_2!)%A_2 \quad B_1 \lt A_1 \quad B_2 \lt A_2$
$$
\begin{gathered}
\because B! \cdot (B+1) \cdot (B+2) \cdot (B+3) \cdots (A-1)\ % \ A=−1\ \ %\ A
\
\therefore B!\ %\ A = [-(B+1) \cdot (B+2) \cdot (B+3) \cdots (A-1)]^{-1} \pmod A
\end{gathered}
$$
求出逆元可得 $ p、q 、r $。

7.5.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
from base64 import b64decode
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
from Crypto.Util.number import inverse, long_to_bytes
from sympy import totient, nextprime
from math import prod

def product_b_to_a(A, B):
    ans = 1
    temp = pow(-1, 1, A)
    for i in range(B+1, A):
        ans = (ans * inverse(i, A)) % A
    return (ans * temp) % A


def standard_rsa_decryption(e, c, primes=None, n=None, phi=None, ct_format='int'):
    """
    标准 RSA 解密
    """
    if not phi:
        if n:
            phi = totient(n)
        else:
            phi = prod(p - 1 for p in primes)
            n = prod(p for p in primes)

    d = inverse(e, phi)
    
    if ct_format == 'base64':
        p, q = primes[0], primes[1]
        key_info = RSA.construct((n, e, d, p, q))
        key = RSA.importKey(key_info.exportKey())
        key = PKCS1_OAEP.new(key)
        m = key.decrypt(b64decode(c)).decode()
    else:
        m = pow(c, d, n)

    return m


if __name__ == '__main__':
    A1 = 21856963452461630437348278434191434000066076750419027493852463513469865262064340836613831066602300959772632397773487317560339056658299954464169264467234407
    B1 = 21856963452461630437348278434191434000066076750419027493852463513469865262064340836613831066602300959772632397773487317560339056658299954464169264467140596
    A2 = 16466113115839228119767887899308820025749260933863446888224167169857612178664139545726340867406790754560227516013796269941438076818194617030304851858418927
    B2 = 16466113115839228119767887899308820025749260933863446888224167169857612178664139545726340867406790754560227516013796269941438076818194617030304851858351026
    n = 85492663786275292159831603391083876175149354309327673008716627650718160585639723100793347534649628330416631255660901307533909900431413447524262332232659153047067908693481947121069070451562822417357656432171870951184673132554213690123308042697361969986360375060954702920656364144154145812838558365334172935931441424096270206140691814662318562696925767991937369782627908408239087358033165410020690152067715711112732252038588432896758405898709010342467882264362733
    e = 0x1001
    c = 75700883021669577739329316795450706204502635802310731477156998834710820770245219468703245302009998932067080383977560299708060476222089630209972629755965140317526034680452483360917378812244365884527186056341888615564335560765053550155758362271622330017433403027261127561225585912484777829588501213961110690451987625502701331485141639684356427316905122995759825241133872734362716041819819948645662803292418802204430874521342108413623635150475963121220095236776428

    p = nextprime(product_b_to_a(A1, B1))
    q = nextprime(product_b_to_a(A2, B2))
    r = n // p // q

    pt = standard_rsa_decryption(e, c, [p, q, r])
    print(long_to_bytes(pt))

    # b'RoarCTF{wm-CongrAtu1ation4-1t4-ju4t-A-bAby-R4A}'

7.6 [WUSTCTF2020]大数计算

7.6.1 题目

1
2
3
4
5
flag等于 wctf2020{Part1-Part2-Part3-Part4} 每一Part都为数的十六进制形式（不需要0x)，并用 '-' 连接
Part1 = 2020*2019*2018* ... *3*2*1 的前8位
Part2 = 520^1314 + 2333^666 的前8位
Part3 = 宇宙终极问题的答案 x,y,z绝对值和的前8位
Part4 = 见图片附件，计算结果乘上1314

7.6.2 解题思路

按照要求写脚本。

7.6.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from sympy import symbols, integrate
from math import factorial

if __name__ == '__main__':
    part1 = str(factorial(2020))[:8]
    part2 = str(520**1314 + 2333**666)[:8]
    part3 = str(sum(map(abs, [-80538738812075974, 80435758145817515, 12602123297335631])))[:8]

    x = symbols('x')
    part4 = str((integrate(2 * x, (x, 0, 22)) + 36) * 1314)

    flag = f"wctf2020{{{int(part1):x}-{int(part2):x}-{int(part3):x}-{int(part4):x}}}"
    print(flag)

    # wctf2020{24d231f-403cfd3-108db5e-a6d10}

7.7 救世捷径

7.7.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
一个名叫CPU的神秘大陆有26个国家，有些国家之间会有一条无向路，每条路径都有不同的长度和一段神秘代码，救世主尼奥要从国家1出发，赶往国家26拯救大陆，请你帮助救世主选择最短路径，而走过的路的神秘代码连接起来便是flag。 以下是数行数据，每行第一个，第二个数字代表这条路的两个端点国家，第三个数字代表路途长度，最后一个字符串便是神秘代码。路在附件中~ 帮助救世主尼奥吧，他快被吓尿了。。。

1 2 100 FLAG{
2 3 87 AFQWE
2 4 57 ETKLS
2 5 50 WEIVK
2 6 51 AWEIW
3 7 94 QIECJF
3 8 78 QSXKE
3 9 85 QWEIH
4 13 54 WQOJF
4 14 47 KDNVE
4 15 98 QISNV
5 10 43 AEWJV
5 11 32 QWKXF
5 12 44 ASJVL
6 16 59 ASJXJ
6 17 92 QJXNV
6 18 39 SCJJF
6 23 99 SJVHF
7 19 99 WJCNF
8 20 96 SKCNG
9 20 86 SJXHF
10 21 60 SJJCH
11 21 57 SJHGG
12 22 47 SJCHF
14 10 55 EJFHG
16 17 59 ASJVH
18 12 53 SJFHG
18 24 93 SHFVG
21 22 33 SJFHB
19 25 88 ASHHF
20 25 96 SJVHG
22 25 23 SJVHJ
25 26 75 SDEV}

7.7.2 解题思路

最短路径问题：Dijkstra 算法

7.7.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
import heapq

def dijkstra(graph, start, end):
    """
    Dijkstra 算法，计算加权无向图中从起点到终点的最短路径
    """
    # 初始化距离字典，存储从起点到各节点的最短距离
    distances = {node: float('inf') for node in graph}
    distances[start] = 0
    
    # 初始化前驱节点字典，用于回溯最短路径
    predecessors = {node: None for node in graph}
    
    # 初始化优先队列（最小堆）
    priority_queue = [(0, start)]
    
    while priority_queue:
        current_distance, current_node = heapq.heappop(priority_queue)
        
        # 如果到达终点，结束算法
        if current_node == end:
            break
        
        # 如果当前距离大于已记录的最短距离，跳过
        if current_distance > distances[current_node]:
            continue
        
        # 遍历当前节点的所有邻居
        for neighbor, weight, flag in graph[current_node]:
            distance = current_distance + weight
            
            # 如果找到更短的路径，更新距离和前驱节点
            if distance < distances[neighbor]:
                distances[neighbor] = distance
                predecessors[neighbor] = (current_node, flag)
                heapq.heappush(priority_queue, (distance, neighbor))
    
    # 回溯构建最短路径和标记序列
    path = []
    flags = []
    current = end
    
    while current is not None:
        path.append(current)
        if predecessors[current] is not None:
            flags.append(predecessors[current][1])
        current = predecessors[current][0] if predecessors[current] else None
    
    # 反转路径和标记序列，使其按从起点到终点的顺序排列
    path.reverse()
    flags.reverse()
    
    return distances[end], path, flags


if __name__ == "__main__":
    edges = [
        [1, 2, 100, 'FLAG{'],
        [2, 3, 87, "AFQWE"],
        [2, 4, 57, "ETKLS"],
        [2, 5, 50, "WEIVK"],
        [2, 6, 51, "AWEIW"],
        [3, 7, 94, "QIECJF"],
        [3, 8, 78, "QSXKE"],
        [3, 9, 85, "QWEIH"],
        [4, 13, 54, "WQOJF"],
        [4, 14, 47, "KDNVE"],
        [4, 15, 98, "QISNV"],
        [5, 10, 43, "AEWJV"],
        [5, 11, 32, "QWKXF"],
        [5, 12, 44, "ASJVL"],
        [6, 16, 59, "ASJXJ"],
        [6, 17, 92, "QJXNV"],
        [6, 18, 39, "SCJJF"],
        [6, 23, 99, "SJVHF"],
        [7, 19, 99, "WJCNF"],
        [8, 20, 96, "SKCNG"],
        [9, 20, 86, "SJXHF"],
        [10, 21, 60, "SJJCH"],
        [11, 21, 57, "SJHGG"],
        [12, 22, 47, "SJCHF"],
        [14, 10, 55, "EJFHG"],
        [16, 17, 59, "ASJVH"],
        [18, 12, 53, "SJFHG"],
        [18, 24, 93, "SHFVG"],
        [21, 22, 33, "SJFHB"],
        [19, 25, 88, "ASHHF"],
        [20, 25, 96, "SJVHG"],
        [22, 25, 23, "SJVHJ"],
        [25, 26, 75, "SDEV}"]
    ]

    # 构建图的邻接表表示
    graph = {}
    for u, v, w, flag in edges:
        if u not in graph:
            graph[u] = []
        if v not in graph:
            graph[v] = []
        graph[u].append((v, w, flag))
        graph[v].append((u, w, flag))  # 无向图需要双向添加边

    total_weight, path, flags = dijkstra(graph, 1, 26)
    print(''.join(flags))

    # FLAG{WEIVKASJVLSJCHFSJVHJSDEV}

8. 信息隐藏与隐写术

8.1 password

8.1.1 题目

1
2
3
4
姓名：张三 
生日：19900315

key格式为key{xxxxxxxxxx}

8.1.2 解题思路

key{} 中有 10 个数，猜测可能是“姓名缩写+生日”

8.1.3 解题脚本

1
flag{zs19900315}

8.2 [NPUCTF2020]这是什么觅🐎

8.2.1 题目

8.2.2 解题思路

文件改为压缩包格式解压，F1 W1 S22 S21 T12 S11 W1 S13 字母部分对应星期的英文首字母，T1 对应星期二、S1 对应星期六、S2 对应星期日；最后一个数字表示该星期下方的第几个具体日期。最终提取出一组数字 3, 1, 12, 5, 14, 4, 1, 18，对应英文字母表序号还原出 flag。

8.2.3 解题脚本

1
2
3
4
if __name__ == "__main__":
    numbers = [3, 1, 12, 5, 14, 4, 1, 18]
    letters = [chr(n + ord('a') - 1) for n in numbers]
    print(f"flag{{{''.join(letters)}}}")

8.3 [ACTF新生赛2020]crypto-classic0

8.3.1 题目

1
2
3
4
5
6
7
8
# hint.txt
哼，压缩包的密码？这是小Z童鞋的生日吧==

# cipher
Ygvdmq[lYate[elghqvakl}

# howtoencrypt.zip
50 4b 03 04 14 00 01 00 08 00 4b 8f 2c 50 6c f5 eb d9 97 00 00 00 ad 00 00 00 17 00 00 00 68 6f 77 74 6f 65 6e 63 72 79 70 74 2f 63 6c 61 73 73 69 63 30 2e 63 3e ae 1a 0f 42 9f 37 a1 bb 98 91 2b d4 50 3b b4 1d 5f d9 0d 12 b3 4c 9d 1f ac 17 67 0d ef 6b 44 a9 dc df 1d e8 24 a4 11 9b e0 ff dd 78 b3 e9 05 2a 18 22 6f fc 8e 8c b9 cd b4 dd f5 37 c6 29 96 24 96 34 4a ef 35 ef 4f 24 5b 72 4c 0e 97 51 d6 43 3c 97 f3 41 7c 67 be 1f 53 70 ff 8b 0e e6 27 b4 f8 af 85 5a 23 12 a3 93 45 a3 08 f9 55 1f 15 75 7b 27 1d 1e fa a2 40 16 3f 6b 60 ff 14 87 54 1a eb 3a 99 2b 00 a1 00 2c e8 83 09 68 66 77 7c 34 20 83 08 ea 78 61 50 4b 03 04 14 00 00 00 00 00 3d 90 2c 50 00 00 00 00 00 00 00 00 00 00 00 00 0d 00 00 00 68 6f 77 74 6f 65 6e 63 72 79 70 74 2f 50 4b 01 02 3f 00 14 00 01 00 08 00 4b 8f 2c 50 6c f5 eb d9 97 00 00 00 ad 00 00 00 17 00 24 00 00 00 00 00 00 00 20 00 00 00 00 00 00 00 68 6f 77 74 6f 65 6e 63 72 79 70 74 2f 63 6c 61 73 73 69 63 30 2e 63 0a 00 20 00 00 00 00 00 01 00 18 00 da 42 47 d2 2e c9 d5 01 c3 2c 95 53 2f c9 d5 01 9c a4 55 af 2e c9 d5 01 50 4b 01 02 3f 00 14 00 00 00 00 00 3d 90 2c 50 00 00 00 00 00 00 00 00 00 00 00 00 0d 00 24 00 00 00 00 00 00 00 10 00 00 00 cc 00 00 00 68 6f 77 74 6f 65 6e 63 72 79 70 74 2f 0a 00 20 00 00 00 00 00 01 00 18 00 29 e8 fc 52 2f c9 d5 01 63 6e 2d 61 2f c9 d5 01 5f b5 56 af 2e c9 d5 01 50 4b 05 06 00 00 00 00 02 00 02 00 c8 00 00 00 f7 00 00 00 00 00

8.3.2 解题思路

压缩包爆破，Archive 爆破 8 位数字（YYYYMMDD）获得压缩包密码 19990306。获得 flag 加密算法文件：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include<stdio.h>

char flag[25] = ***

int main()
{
    int i;
    for(i=0;i<25;i++)
    {
        flag[i] -= 3;
        flag[i] ^= 0x7;
        printf("%c",flag[i]);
    }
    return 0;
}

简单逆向算法即可。

8.3.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def reverse(ciphertext):
    res = ''
    for ct in ciphertext:
        ascii_val = ord(ct)
        ascii_val ^= 7
        ascii_val += 3
        res += chr(ascii_val)
    return res

if __name__ == '__main__':
    ciphertext = 'Ygvdmq[lYate[elghqvakl}'
    print(reverse(ciphertext))

    # actf{my_naive_encrytion}

8.4 [ACTF新生赛2020]crypto-rsa0

8.4.1 题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
怎么办呢，出题人也太坏了，竟然把压缩包给伪加密了！

# challenge.zip
50 4B 03 04 14 00 09 00 08 00 72 93 77 4F D0 36
EB 71 3F 01 00 00 6C 02 00 00 10 00 00 00 63 68
61 6C 6C 65 6E 67 65 2F 6F 75 74 70 75 74 15 92
4B 0E 84 30 0C 43 F7 23 71 17 E7 E3 38 B9 FF C5
C6 95 00 41 48 63 FB B5 87 58 EE 62 A6 AB 13 53
52 36 52 8A C9 D6 A8 2E 15 B5 FE 40 A8 B0 3B 1A
E6 E4 B1 82 31 75 87 9B AD 16 32 2F 73 3B F2 2E
72 53 4D 46 AF 8B D3 EE C1 BA 35 4B C1 5A B7 5F
DF B4 2C 59 13 57 CB 3A 6D F3 CE 73 06 19 E8 88
EF 27 FA 13 B4 89 95 FC 48 6A 8B CA D3 00 A5 67
24 AA DA EF 33 37 45 68 A6 B2 6D 24 DE DC 0A DD
55 46 33 D2 8D 98 A5 B4 44 C3 69 02 51 42 97 97
1D 37 1D CC 42 B7 BE C2 77 5B A4 98 88 3E EB 0D
88 97 22 C5 50 3B 68 7D 3F E2 6E CC EB 92 37 1E
76 1D 4C 3E 5F 75 2F 18 5D 70 94 89 B6 F1 21 2A
75 09 13 7C 7A ED 55 2B C2 FD 72 18 E3 34 7E E7
CF EA 5D 4E 92 14 D7 C4 C7 75 D0 84 FC C3 4D 07
6F 90 D1 55 0C C3 2D B0 22 8D AD D4 B7 8E D8 9E
B5 66 F0 D8 2F CA 03 F7 A0 0D 9B EF 1E 94 F5 B3
1C 4F 06 DC AB E7 65 CB 82 3B B1 61 9C D6 B0 67
1B 27 01 98 F3 B9 5C B6 9E A6 82 3D 1F 13 23 31
F0 6D FB 48 CF D3 3B 33 B6 6B 87 B1 76 A1 4C 39
49 9F C3 B6 D6 FB EC CA 63 62 2D FC 01 50 4B 03
04 14 00 09 00 08 00 1D B8 30 50 C8 5D 92 54 B1
00 00 00 F1 00 00 00 11 00 00 00 63 68 61 6C 6C
65 6E 67 65 2F 72 73 61 30 2E 70 79 55 8E 3D 0B
C2 30 10 86 F7 40 FE 43 C0 C1 B4 94 82 4A 75 CA
20 82 2E 52 5C 9C A5 35 D7 1A C8 57 D3 A8 F4 DF
7B 11 3B C8 2D CF DD BD F7 70 5D 70 86 1D C2 E4
A3 93 CE 40 79 8D 4A 97 F6 69 5A 08 4C 19 EF 42
64 39 25 3F 0A 8D C5 10 25 94 1C CF FB 93 58 3C
94 94 60 0B E6 35 34 23 B0 D1 E9 17 30 15 29 E9
74 D3 0B 65 63 99 F4 B7 76 8A 30 F2 74 52 24 74
41 A2 5C B0 65 AB FA 65 86 36 2C 2F 7A 88 97 A0
0C F0 6A B5 C6 E1 F0 3F F8 66 02 1A B9 CF 66 1A
90 6A E1 F3 81 12 10 DB AA DA EC 10 EC 1D CD DE
BD 79 7A A1 80 A2 9E E3 8C E3 0E 9B 0F 50 4B 03
04 14 00 09 00 00 00 45 B8 30 50 00 00 00 00 00
00 00 00 00 00 00 00 0A 00 00 00 63 68 61 6C 6C
65 6E 67 65 2F 50 4B 01 02 3F 00 14 00 00 00 08
00 72 93 77 4F D0 36 EB 71 3F 01 00 00 6C 02 00
00 10 00 24 00 00 00 00 00 00 00 20 00 00 00 00
00 00 00 63 68 61 6C 6C 65 6E 67 65 2F 6F 75 74
70 75 74 0A 00 20 00 00 00 00 00 01 00 18 00 F7
03 9A 9E E8 A1 D5 01 C9 09 90 EC 7D CC D5 01 66
E3 8F EC 7D CC D5 01 50 4B 01 02 3F 00 14 00 09
00 08 00 1D B8 30 50 C8 5D 92 54 B1 00 00 00 F1
00 00 00 11 00 24 00 00 00 00 00 00 00 20 00 00
00 6D 01 00 00 63 68 61 6C 6C 65 6E 67 65 2F 72
73 61 30 2E 70 79 0A 00 20 00 00 00 00 00 01 00
18 00 10 04 2F C1 7D CC D5 01 53 57 DD EC 7D CC
D5 01 7C 56 90 EC 7D CC D5 01 50 4B 01 02 3F 00
14 00 00 00 00 00 45 B8 30 50 00 00 00 00 00 00
00 00 00 00 00 00 0A 00 24 00 00 00 00 00 00 00
10 00 00 00 4D 02 00 00 63 68 61 6C 6C 65 6E 67
65 2F 0A 00 20 00 00 00 00 00 01 00 18 00 7C 56
90 EC 7D CC D5 01 9D 1F 39 01 7E CC D5 01 54 47
8F EC 7D CC D5 01 50 4B 05 06 00 00 00 00 03 00
03 00 21 01 00 00 75 02 00 00 00 00

8.4.2 解题思路

压缩包伪加密，压缩文件中的目录区标记 50 4B 01 02，定位到目录文件头。后面的字段中，00 00 表示未启用加密（该字段为全局方式标志位，奇数表示加密，偶数表示未加密）。可使用 010 Editor 将第二个 50 4B 01 02 后的 09 00 修改为 00 00，以解除加密标志。

解压得到加密脚本：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from Cryptodome.Util.number import *
import random

FLAG=#hidden, please solve it
flag=int.from_bytes(FLAG,byteorder = 'big')


p=getPrime(512)
q=getPrime(512)

print(p)
print(q)
N=p*q
e=65537
enc = pow(flag,e,N)
print(enc)

9018588066434206377240277162476739271386240173088676526295315163990968347022922841299128274551482926490908399237153883494964743436193853978459947060210411
7547005673877738257835729760037765213340036696350766324229143613179932145122130685778504062410137043635958208805698698169847293520149572605026492751740223
50996206925961019415256003394743594106061473865032792073035954925875056079762626648452348856255575840166640519334862690063949316515750256545937498213476286637455803452890781264446030732369871044870359838568618176586206041055000297981733272816089806014400846392307742065559331874972274844992047849472203390350

标准 RSA 解密

8.4.3 解题脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
from math import prod
from sympy import totient
from base64 import b64decode
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
from Crypto.Util.number import inverse, long_to_bytes


def standard_rsa_decryption(e, c, primes=None, n=None, phi=None, ct_format='int'):
    """
    标准 RSA 解密
    """
    if not phi:
        if n:
            phi = totient(n)
        else:
            phi = prod(p - 1 for p in primes)
            n = prod(p for p in primes)

    d = inverse(e, phi)
    
    if ct_format == 'base64':
        p, q = primes[0], primes[1]
        key_info = RSA.construct((n, e, d, p, q))
        key = RSA.importKey(key_info.exportKey())
        key = PKCS1_OAEP.new(key)
        m = key.decrypt(b64decode(c)).decode()
    else:
        m = pow(c, d, n)

    return m


if __name__ == '__main__':
    e = 65537
    p = 9018588066434206377240277162476739271386240173088676526295315163990968347022922841299128274551482926490908399237153883494964743436193853978459947060210411
    q = 7547005673877738257835729760037765213340036696350766324229143613179932145122130685778504062410137043635958208805698698169847293520149572605026492751740223
    c = 50996206925961019415256003394743594106061473865032792073035954925875056079762626648452348856255575840166640519334862690063949316515750256545937498213476286637455803452890781264446030732369871044870359838568618176586206041055000297981733272816089806014400846392307742065559331874972274844992047849472203390350
    print(long_to_bytes(standard_rsa_decryption(e, c, [p, q])))

    # b'actf{n0w_y0u_see_RSA}'

[日常训练] Crypto Training - BUUCTF（一）

http://dstbp.com/2024/02/01/buuctf1/

作者

DSTBP

发布于

2024-02-01

更新于

2025-07-12

许可协议

CC BY 4.0

#

喜欢这篇文章？打赏一下作者吧

评论

GitHub
微信二维码

归档

目录

最新文章

最新评论

×