序言 最近发现一个在线塔防策略游戏网站:https://yorg.io/ ,基本玩法是昼夜交替的生存挑战 ,如图 1.1 所示,玩家需白天建立资源供应链,包括采矿(水晶、铁矿、铀矿等)、运输(通过运输机连接建筑)和工厂生产(如炮弹、弓箭、护盾等),为夜晚防御做准备,晚上僵尸从地图边界进攻,玩家需通过防御塔(箭塔、加农炮、闪电塔等)和城墙抵御攻击。每 10 天会刷新强力 BOSS。
图 0.1 yorg 游戏界面 游玩时发现可以本地存档,下次游玩时加载存档文件继续上次进度。作为一名网安狗,当即就想到修改存档改变数值,达到无限水晶和技能点的效果。
通过打开开发者工具并跟踪保存存档的过程,我们可以定位到具体的保存函数。这里不展开具体的跟踪步骤,基本思路是:以存档文件名为关键词进行搜索,找到触发保存的函数,再向下追踪调用栈,分析可知网页逻辑是先将存档数据保存到 localStorage 中,通过索引 savegame_blob_xxxx 查找对应的存档数据,再执行保存文件的操作。搜索关键词 savegame_blob_ 找到处理函数,逻辑流程如下:this.root.savegames.saveGame() → updateLastSavegame() → dataToString(t) →compressToEncodedURIComponent(t) → _compress(t)。
图 0.2 _compress 函数调试 如图 1.2 所示,分析_compress() 可知这是一个 LZW 压缩算法,那么什么是 LZW 压缩算法呢?
1. 原理 LZW 其实是三个大佬的名字,这个算法最开始是 Ziv 和 Lempel 这两个人于 1977,1978 年发明,在 1984 年的时候由 Terry Welch 进行了改进,由此得名 LZW 编码(Lempel-Ziv-Welch Encoding),属于 LZ78 编码的变种。简单来说,LZW 算法就是通过建立一个字符串表,将多次出现的字符串存到表中并编号,用较短的编号表示较长的字符串来实现压缩。也被称为串表压缩算法。
1.1 示例 1.1.1 编号的映射 假设我们要通过互联网传输一本英文牛津字典。按照常规方式,一个字符占 1 字节,这本字典大约包含 60 万个单词(包括重复的),每个单词平均 5 个字母,总共约 300 万个字符,也就是 300 万字节的数据量。
但如果我们换种思路:先提取出不重复的单词,假设有 20 万个唯一单词。我们给每个单词编上一个编号,比如从 1 开始。只需 3 个字节(24 位)就能唯一表示一个编号($ 2^{24} \gt 200000 $)。这样,每个单词只需用 3 个字节的编号代替原始文本。对于总共 60 万个单词,传输只需 60 万 × 3 = 180 万字节。相比原来的 300 万字节,这种方法节省了超过三分之一的数据量。
LZW 编码也是同理,把出现过的字符串映射到编号上,实现压缩。例如对于字符串:ABABAB,可以看到子串 AB 多次重复, 我们可以用一个特殊的符号(比如数字 2)来表示 AB ,那么原来的字符串就可以表示为:AB22。在这个例子中,数字 2 被称为子串 AB 的符号 (Symbol)。那 A 和 B 本身有没有符号?当然有。我们可以规定 0 表示 A,1 表示 B。于是最终压缩后的数据是一个符号流 (Symbol Stream):0122。
当然在真实的 LZW 编码中,A 和 B 不会用 0 和 1 表示,而是直接用它们的 ASCII 值。LZW 的初始字典包含所有 256 个 ASCII 字符,这些字符的符号就是它们各自的 ASCII 值。从 256 开始,编码过程中会动态添加新的字符串映射,这部分称为扩展字典 (Extended Dictionary)。上面案例中在 LZW 编码会转成:65 (A) 66 (B) 257 (AB)。
1.1.2 字典的自解释 有同学可能会问:为什么第一个 AB 不也用 2 表示?这样不又节省了一个符号?这个问题正好引出了 LZW 的一个核心思想:压缩后的数据是自解释的(self-explaining) 。 在 LZW 编码中,压缩数据本身不包含完整的字典。也就是说,压缩文件里并不会存放“2 → AB”这种映射关系。LZW 编码、解码中除了初始字典(0 → A 和 1 → B),不会带有任何关于扩展字典的映射。
回到上面的示例。其编码过程(概念简化版)如下:
读到 A → 查初始字典:A 的符号是 0,输出 0
读到 B → 查初始字典:B 的符号是 1,输出 1
发现 AB 是一个新组合 → 添加到字典中,记符号 2 → AB
再读到 AB → 字典中已有,输出符号 2
再读到 AB → 再次输出符号 2
那解码器是怎么知道符号 2 代表 AB 的?答案是:它在解码的过程中自己“推出来”的 。LZW 的解压过程和编码一样,从初始字典出发,一边根据已经解出的内容动态构建字典一边解码。
当我们解码 0122 时,解码器的过程(概念简化版)是:
0 → 查初始字典:0 对应 A,输出 A
1 → 查初始字典,1 对应 B,输出 B
遇到 2,初始字典中没有,根据前两个输出是 A 和 B → 创建新映射:2 → AB
2 → AB,输出 AB
2 → AB,输出 AB
现在就解释为什么前面不能直接用 2。因为在前两个字符 A 和 B 被编码输出之前,AB 组合还不存在于字典中。一开始就用 2 表示 AB,解码器看到“2”时会不知道它指的是什么,它还没从前文推导出 2 → AB 的关系。所以前面的 0 和 1 不只是输出结果,它们本身就是构建后续字典的“依据” ,是字典构建的“第一现场”。这就是“自解释”:压缩后的数据本身就包含了解压所需的全部信息,压缩时使用的字典不需要另外传输或存储。
1.2 算法详解 下面我们通过一个稍微复杂的例子,完整展示 LZW 编码与解码的全过程,重点是理解:在解码时,每一步是如何对应编码过程中的操作,以及如何一步步还原原始字符串并重建编码时使用的字典。
1.2.1 编码算法 编码器在处理原始字符串时,会不断读取新字符,并尝试将已有的字符串或组合进行编码。为了实现这一过程,我们维护两个变量:
P(Previous) :当前已读取、尚未编码的字符串片段。C(Current) :刚读入的新字符。
编码器的工作是将 P+C 这个组合查找字典,如果存在,就继续向后读取字符并扩展;如果不存在,就将 P 对应的符号输出,并将 P+C 加入字典。具体编码流程如下:
初始化:字典中只包含所有单字符的默认项,例如 0 → a,1 → b,2 → c 等。此时变量 P 和 C 均为空。
读取字符:读入一个新字符赋值给 C,然后将 P 和 C 合并为字符串 P+C。
字典查找:检查 P+C 是否在字典中:
如果存在,则将 P 更新为 P+C。
如果不存在,输出 P 对应的符号,在字典中建立 P+C 映射,并将 P 更新为 C。
重复处理:返回第 2 步,继续处理下一个字符,直到整个输入字符串处理完毕。
到达字符串尾部,没有新的 C 读入时,则将 P 对应的符号输出,结束。
图 1.1 LZW 编码流程图 LZW 编码的关键就在第 3 步 —— 理解变量 P 是什么。P 是当前维护的、可以被编码为符号的子串,但还没有输出 。随着每读入一个新字符 C,我们尝试把它加到 P 的末尾,形成新的组合 P+C。只要这个组合还能在字典中找到,我们就不断更新 P = P+C,也就是说,我们在试图找到尽可能长的子串将其编码为一个符号,这就是压缩的实现。一旦 P+C 不在字典里了,就意味着当前这段子串没办法再长了。此时我们:
输出当前 P 的编码符号。
把 P+C 加入字典,作为一个新的子串项。
把 P 重新设为 C,重新开始构建新的子串。
通过这种方式,我们就能把较长、重复的子串用一个符号表示,从而达到压缩的效果。至于为什么输出的是 P,是因为 P+C 还没被收录进字典,还没有符号可以输出。只能把已有的 P 输出,再把 P+C 加进去,以备后面用到。
举个例子,对于一个字符串:ababnababan,初始状态字典里有三个默认的映射,如表 1.1 所示:
Symbol
String
0
a
1
b
2
n
表 1.1 编码初始字典 开始编码,编码步骤如表 1.2 所示:
Step
P
C
P+C
P+C in Dict ?
Action
Output
1
-
a
a
Yes
更新 P=a
-
2
a
b
ab
No
添加 3 → ab,更新 P=b
0
3
b
a
ba
No
添加 4 → ba,更新 P=a
1
4
a
b
ab
Yes
更新 P=ab
-
5
ab
n
abn
No
添加 5 → abn,更新 P=n
3
6
n
a
na
No
添加 6 → na,更新 P=a
2
7
a
b
ab
Yes
更新 P=ab
-
8
ab
a
aba
No
添加 7 → aba,更新 P=a
3
9
a
b
ab
Yes
更新 P=ab
-
10
ab
a
aba
Yes
更新 P=aba
-
11
aba
n
aban
No
添加 8 → aban,更新 P=n
7
12
n
-
-
-
-
2
表 1.2 编码过程步骤跟踪表 输出的结果为 0132372,完整的字典如表 1.3 所示:
Symbol
String
0
a
1
b
2
n
3
ab
4
ba
5
abn
6
na
7
aba
8
aban
表 1.3 映射字典 图 1.2 展示原字符串是如何对应到压缩后的编码,图 1.3 展示 LZW 编码如何保存映射到字典中。
图 1.2 原字符串对应压缩后编码 图 1.3 字符串字典映射 1.2.2 解码算法 读到这里,可能大家有一个疑惑,为什么要这么设计字典映射与编码?这其实都是为解码做准备,解码的过程比编码复杂,其核心思想在于解码需要还原出编码时的用的字典,即如何对应编码的过程。
在 LZW 解码中,输入是压缩后的符号流(Symbol Stream)。和编码类似,解码过程也维护两个变量:
pW(previous word) :前一个解码出来的符号 。cW(current word) :当前新读取的符号 。
这里的“W”可以理解为一个符号。每个符号代表一个已知的字符串片段。用 Str(cW) 和 Str(pW) 表示它们解码出来的原字符串。
初始化:字典中只包含默认的初始字典,例如 0 → a,1 → b,2 → c 等。此时变量 pW 和 cW 都为空。
读取第一个字符:第一个符号一定能直接在字典中找到,它代表一个单个字符。解码后输出该字符。
将 pW 设为 cW。
读取下一个符号 cW。
判断 cW 是否存在于字典中:
如果存在:
解码并输出 Str(cW)。
令 P = Str(pW),C = Str(cW) 的第一个字符 。
将新组合 P + C 加入字典,分配一个新的符号。
如果不存在:
令 P = Str(pW),C = Str(pW) 的第一个字符 。
创建新项 P + C,当前 cW 所映射的正是这个新字符串,加入字典。
输出 P + C。
回到第 3 步,继续处理下一个符号,直到读完整个符号流。
图 1.4 LZW 解码流程图 显然,第 5 步是解码过程的关键,也是最难理解的一步。在这一阶段,解码器不仅在解析符号,更重要的是它一边解码,一边模拟编码时的字典构建过程。下面详细阐述 0132372 解码成 ababnababan 的流程:
与编码一样,解码时初始状态字典里只有三个默认的映射,如表 1.4 所示:
Symbol
String
0
a
1
b
2
n
表 1.4 解码初始字典 开始解码,解码步骤如表 1.5 所示:
Step
pW
cW
cW in Dict ?
Action
Output
1
-
0
Yes
C=a,pW=0
a
2
0
1
Yes
P=a,C=b,P+C=ab,添加 3 → ab
b
3
1
3
Yes
P=b,C=a,P+C=ba,添加 4 → ba
ab
4
3
2
Yes
P=ab,C=n,P+C=abn,添加 5 → abn
n
5
2
3
Yes
P=n,C=a,P+C=na,添加 6 → an
ab
6
3
7
No
P=ab,C=a,P+C=aba,添加 7 → aba
aba
7
7
2
Yes
P=aba,C=n,P+C=aban,添加 8 → aban
n
表 1.5 解码过程步骤跟踪表 仔细观察新映射是如何添加到字典中的,我们可以看到,解码器其实是在一步步“重演”编码器的操作 ,从而还原出编码过程。
如果新读入的 cW 能在字典里找到,那就能直接解码 cW,然后一边解码(输出 Str(cW)),一边构建新的映射(Str(pW) + Str(cW) 第一个字符)。
如果 cW 不在字典中,这时就需要解码器做出一个推理,我们来看 Step 6:
cW=7,7 还没出现在字典里,但根据之前 cW 能在字典找到的情况,解码器可以推理出 7 映射的新字符串应该是当前的 Str(pW),也就是 ab,以及未知的 Str(cW) 第一个字符拼接而成。而 cW 映射的就是这个即将新加入的字符串:Str(pW) + Str(cW)[0],所以 cW 的第一个字符就是 Str(pW) 的第一个字符 a,所以 Str(cW) = aba。
知道了怎么处理,现在思考为什么 cW 解码时,其还没有在字典里建立映射?因为字典中新条目总是比编码“晚一步”生成 ,如表 1.6 所示,编码器在输出某个符号时,已经读取了后面的字符,并基于它构建了下一条字典项。
Step
已有字符串 P
读到的字符 C
Output
新增映射
1
a
b
0 (a → 0)
添加 3 → ab
2
b
a
1 (b → 1)
添加 4 → ba
3
ab
n
3 (ab → 3)
添加 5 → abn
4
n
a
2 (n → 2)
添加 6 → na
5
ab
a
3 (ab → 3)
添加 7 → aba
6
aba
n
7 (aba → 7)
添加 8 → aban
7
n
-
2 (n → 2)
-
表 1.6 编码过程构建字典与编码时序表(只列关键步骤) 而解码则不同,如表 1.7 所示,解码器先读符号再解码,根据解码的结果构建映射。
Step
读到的字符
字典是否存在
Output
新增映射
1
0
Yes
a
-
2
1
Yes
b
添加 3 → ab
3
3
Yes
ab
添加 4 → ba
4
2
Yes
n
添加 5 → abn
5
3
Yes
ab
添加 6 → an
6
7
No
ab + a
添加 7 → aba
7
2
Yes
n
添加 8 → aban
表 1.7 解码过程构建字典与解码时序表(只列关键步骤) 所以编码器写入字典的映射,解码器总要等到下一轮才会写入。而当要新增的映射恰好在同一轮被引用时,就出现了先拿到符号但是还没建立这个映射的情况。这其实就是遇到了编码器刚刚创建但还没来得及传达其含义的字典项 。这时就需要根据当前上下文,靠 Str(pW) + Str(pW)[0] 来还原原意。
1.3 中文 LZW 1.3.1 挑战与研究现状 以上的分析主要基于英文文本的压缩场景。那么在中文语境下,LZW 又该如何应用呢?首先我们得分析中文文本和西文文本的不同之处:
比较维度
西文文本
中文文本
字符集与编码
字符集小,编码简单,单字符占字节少
字符集大,编码复杂,单字符占字节多
语言结构与语法规则
词与词间用空格等分隔符分开,词边界清晰,语法规则固定
需分词,语法灵活,分析难度大
统计特性
字符出现频率相对分散,不同字符使用频率有差异但不悬殊
不同汉字使用频率差异极大,常用字频率高,生僻字频率低
表 1.8 中西文特点对比 对 LZW 算法的中文文本压缩的应用而言,最简单的做法是直接套用通用的 LZW 算法。但这方法缺点在于通用算法以字节为基本处理单位,压缩过程中会人为地割裂中文数据编码中蕴含的语义信息,导致压缩比偏低。对此,徐秉铮[1] 、华强[2] 等人从数据读取方式和基础码集结构出发,调整算法以适配汉字的编码和大字符集特性,压缩效果有所提升,但仍远低于 LZW 算法对英文文本的压缩比。陈庆辉[3] 等人在现有基础算法上进行改进,提高了由于中文文本中重复字串不长导致压缩比远低于英文文本的压缩比例,压缩效果显著增强。
1.3.2 详细算法 本文采用陈庆辉等人的中文文本压缩算法,其算法基于最大字典编码长度为 19 位的 LZW 传统算法,将 GB2312-80 标准字符中的一级汉字和第 1、3 区的常用字符存入初始字典。并针对中文文本重复字串不长的特点,对字典码值进行双模式变长编码 输出,具体编码输出方法如下:
按码值的最小二进制表示位数对字典进行分段,则字典可分为 19 段。其中码值 $ 2^{n-1}-1 \sim 2^n-1 $ 为字典的第 $ n $ 段。记当前字典中码值的最大长度为 $ n $,其中 $ 11 \lt n \lt 20 $。
当 $ n \lt 14 $ 时,码值采用该码值大小的二进制编码输出,输出长度为 $ n $ 位。
当 $ n = 14 $ 时,开始启用“双模式编码”:
字典中 1 - 12 段的码值:用 13 位表示,首位是 0,后 12 位是实际的码值二进制。
字典中第 13 和 14 段的码值:用 15 位表示,首位是 1,后 14 位为码值。
当 $ n \lt 18 $ 时,前 n-3 段的码值用 n-2 位表示,首位是 0。最后 3 段的码值用 n+1 位表示,首位是 1。
当 $ n \lt 20 $ 时,前 n-4 段的码值用 n-3 位表示,首位是 0。最后 4 段的码值用 n+1 位表示,首位是 1。
这么做的意义在于,大部分数据(常用词)用小编号的码值,而这些码值属于字典的前段。用更短的二进制位表示这些高频码值,就可以整体减少压缩文件的大小。而较大的码值本身出现得少(不常用字符串),即使编码更长,对整体影响也很小。
1.4 改进方案 LZW 算法的解压过程无需在压缩后的数据中添加任何辅助信息就能够自动还原字典,从而保证较快的编解码速度。不过它也不是完美的。其性能容易受到一些因素影响,下面将分析相关影响因素并提出改进方案[4-5] 。需要注意的是,不同的应用场景对压缩效率、速度和资源占用的要求不同,因此改进方法并没有统一的标准,必须根据具体需求选择最合适的方案。
1.4.1 编码方式 LZW 算法通过构建一个字典,用索引替代重复的字符串,在编码方面:
如果用定长编码 (Fixed-Length Coding),初始时就要预留足够多的位数来表示所有可能的索引值,此时高位数的编码会浪费大量内存空间,在设备的内存受限情况下,可能导致性能下降甚至系统崩溃。
而用变长编码 (Variable-Length Coding),在压缩初期能用短位匹配大量重复短字符串,后期用长位处理复杂长字符串组合。且当字典容量扩展时,索引所需的二进制位数同步增加。能更灵活地适配实际情况。
举个例子压缩 ABABABAB 字符串时,固定长度编码和变长编码差异显著。固定长度编码一开始就用 3 位编码,能表示 8 个索引,但实际初期仅用 4 个,高位闲置,内存浪费;而变长编码初期用 2 位编码,在字典满 4 个条目后,动态扩展为 3 位编码,前期节省编码长度,后期也能处理复杂情况,避免了固定编码的内存浪费。
所以,在内存受限的环境中,更推荐使用变长编码 ,动态调整每个索引所占的位数,既保证压缩效果,又节省内存和存储空间。
1.4.2 字典大小 LZW 算法中,字典大小的选择会直接影响压缩效果和处理速度:
字典越大 :能存更多字符串,匹配到的内容更长,压缩效果更好。但缺点是查找匹配的时间会变长,压缩过程更慢。字典越小 :只能匹配较短的字符串,压缩效果变差,但处理速度快,适合对时效性要求高的场景。
因此,字典大小的设置要根据应用场景权衡:
如果用于实时传输(如网络通信),建议用较小的字典,提高压缩速度。
如果用于文件存储或归档,建议用较大的字典,提高压缩率,节省空间。
需要注意的是:字典大小主要影响压缩过程 。而在解压时,只需按编码值查表恢复原始字符串,不涉及复杂匹配,因此对字典大小不太敏感。
1.4.3 搜索方式 LZW 算法的核心在于字典的构建和查找,其性能高度依赖于搜索效率。不同的搜索方式直接影响压缩和解压的速度与资源消耗。常见的三种搜索方式包括:串行搜索、并行搜索和哈希表搜索。
串行搜索
串行搜索是最基础的做法。每次查找新子串时,从字典头部开始一项一项地查找,直到找到匹配项或遍历完整个字典。这种简单,但在字典较大时效率很低,压缩速度慢。
并行搜索
将整个字典拆分为多个子字典,每个子字典可以独立、同时进行查找。这样可以并行处理多个搜索请求,提高速度。通常,第一个子字典为“虚拟字典”,只记录基本字符(如 0–255),不占内存。其余子字典按照不同的字宽(表示的子串长度)划分,可以分布在不同的硬件单元上并行查找,从而提升处理速度。其缺点是控制逻辑更复杂,每次输出不仅要包含子字典的索引,还要记录其在子字典中的位置,编码格式也更复杂。
哈希表搜索
哈希表搜索通过“前缀字符 + 新字符”组合成一个关键字,再用哈希函数直接计算出字典位置,实现快速定位。这种方法查找速度快,但有两个问题需要注意:
哈希函数设计复杂:通常涉及乘法、取余等操作,对硬件不太友好。
哈希冲突不可避免:不同关键字可能映射到同一个地址。为此需要采用开放寻址或链表法等方式解决冲突,但都无法完全避免性能损失。
搜索方式
优点
缺点
串行搜索
逻辑简单、易于实现
搜索延时长、占用硬件资源较多
并行搜索
搜索速度快、存储单元利用率高
控制逻辑复杂、编码复杂
Hash 表搜索
搜索延时短、实时性强
占用硬件资源、存在哈希冲突(无法避免)
表 1.9 搜索方式对比 1.4.4 存储结构 传统的编码方法中,每次只能在已有字符串的基础上增加一个字符来扩展,这种方式效率低下,不仅浪费内存,还拖慢处理速度。可以用其他数据结构重构:
Trie 树(前缀树)
以节点数组的形式存储,从根节点出发的一条路径表示一个字符串。每个节点包含以下三个字段:
父节点(parent):表示该节点前缀所在节点的索引;
当前字符(code):对应该节点的字符,一般是其 ASCII 值;
索引(index):该节点在字典中的位置编号。
当遇到一个未在字典中的字符时,只需将其作为新节点添加到 Trie 树中,并继续扩展构建新的分支。
动态数组 + 哈希表
将字典视为动态扩展的数组,每个条目存储完整字符串及其唯一编码,同时通过哈希表加速字符串查找。
有限自动机(DFA)
将字典转换为确定有限自动机,每个状态对应一个字符串,边表示字符输入后的转移路径,终止状态节点返回对应编码,新增状态生成新条目。
存储结构
使用场景
优点
缺点
Trie 树
高频前缀重复的短字符串 内存充足场景
天然支持前缀匹配 无需处理哈希冲突 插入/查询复杂度稳定
内存占用高 字符集大时空间爆炸(如Unicode)
动态数组+哈希表
通用文本压缩 中等规模数据
查找速度快 动态扩展灵活 实现简单
哈希冲突影响性能 内存占用较高(需存储完整字符串)
有限自动机(DFA)
高吞吐量实时压缩(如网络流) 固定模式字符串快速匹配
状态转移加速匹配 适合硬件加速
构建和维护复杂度高 内存占用极高
表 1.10 存储结构方式对比 1.4.5 字典更新策略 在 LZW 算法中,字典大小在压缩开始前就已经固定,不能根据文件内容动态调整。这意味着,一旦字典被填满,就无法再添加新的字符串,压缩效率也可能随之下降。为了改善这一问题,常见的做法是采用字典更新机制,在不增加字典大小的前提下继续优化压缩效果。以下是几种常见的更新策略:
字典重置(Dictionary Reset, DR)
当字典满了以后,直接清空除初始字典之外的所有条目,重新开始构建字典。DR 实现简单,重置迅速,但每次重置都会丢失所有已有匹配,导致压缩率瞬间降低,整体压缩效果可能变差。
双字典(Double Dictionary, DD)
为了避免重置带来的压缩效率骤降,DD 方法准备两个字典:
一个正在使用的“满字典”,用于匹配。
一个已重置的“备用字典”,用于接收新字符串。
当备用字典积累到一定程度后,替换旧字典继续使用,旧字典重置接受。这种方式压缩效率过渡平滑,不会突然降低。但需要双倍字典空间,而且新旧切换时可能丢弃高频出现的字符串。
先进先出(FIFO)
FIFO 方法认为最早加入字典的字符串可能与当前数据相关性较低。当字典满了后,按照“先加入先淘汰”的规则,从旧条目开始逐个替换新的字符串。逻辑简单,无需额外空间。但无法区分高频或低频条目,可能误删仍然有用的字符串,影响压缩效率。
最近最少使用(LRU)
LRU 方法更智能,它记录字典中每个字符串的使用频率,一旦字典满了,就移除使用最少的字符串,空出位置给新内容。其能保留最有用的高频字符串,压缩效果更好。但需要持续跟踪和更新每个条目的使用记录,计算复杂度高,运行开销大。
更新方式
优点
缺点
DR
简单、快速
压缩比波动大
DD
平滑过渡
占用双倍内存
FIFO
实现容易
容易误删高频条目
LRU
压缩率高
实现复杂,速度慢
表 1.11 更新方式对比 1.5 代码实现 本文的 LZW 算法实现采用了变长编码、Trie 树结构、哈希表加速查找,并支持最大 19 位字典容量。支持中西文压缩,该算法分别用 Python、Java、JS、Go、C 和 Matlab 实现,并对各版本进行了性能对比测试,评估了其压缩效率和运行速度。
本文的开发环境如表 1.12 所示:
语言
版本
Python
3.10.2
GCC
8.1.0
Java
23.0.1
JavaScript
20.18.1
Go
1.24.2
Matlab
-
表 1.12 开发环境 1.5.1 代码源码 lzw.py
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 import sysimport osimport timefrom collections import dequeMAX_BITS = 19 MAX_SIZE = 1 << MAX_BITS CHINESE_DICT = "的一是了我不人在他有这个上们来到时大地为子中你说生国年着就那和要她出也得里后自以会家可下而过天去能对小多然于心学么之都好看起发当没成只如事把还用第样道想作种开美总从无情己面最女但现前些所同日手又行意动\ 方期它头经长儿回位分爱老因很给名法间斯知世什两次使身者被高已亲其进此话常与活正感见明问力理尔点文几定本公特做外孩相西果走将月十实向声车全信重三机工物气每并别真打太新比才便夫再书部水像眼等体却加电主界门\ 利海受听表德少克代员许稜先口由死安写性马光白或住难望教命花结乐色更拉东神记处让母父应直字场平报友关放至张认接告入笑内英军候民岁往何度山觉路带万男边风解叫任金快原吃妈变通师立象数四失满战远格士音轻目条呢\ 病始达深完今提求清王化空业思切怎非找片罗钱紶吗语元喜曾离飞科言干流欢约各即指合反题必该论交终林请医晚制球决窢传画保读运及则房早院量苦火布品近坐产答星精视五连司巴奇管类未朋且婚台夜青北队久乎越观落尽形影\ 红爸百令周吧识步希亚术留市半热送兴造谈容极随演收首根讲整式取照办强石古华諣拿计您装似足双妻尼转诉米称丽客南领节衣站黑刻统断福城故历惊脸选包紧争另建维绝树系伤示愿持千史谁准联妇纪基买志静阿诗独复痛消社算\ 义竟确酒需单治卡幸兰念举仅钟怕共毛句息功官待究跟穿室易游程号居考突皮哪费倒价图具刚脑永歌响商礼细专黄块脚味灵改据般破引食仍存众注笔甚某沉血备习校默务土微娘须试怀料调广蜖苏显赛查密议底列富梦错座参八除跑" class LZW : def __init__ (self ): self .dict_nodes = [] self .hash_table = {} self .queue = deque() self .next_code = 0 def dict_init (self ): """初始化字典(包含单字节字符和中文字典)""" self .dict_nodes = [(-1 , 0 )] + [(0 , 0 )] * (MAX_SIZE - 1 ) self .hash_table.clear() self .queue.clear() self .next_code = 1 for ch in range (256 ): self .dict_nodes[self .next_code] = (0 , ch) self .hash_table[(0 , ch)] = self .next_code self .queue.append(self .next_code) self .next_code += 1 for c in CHINESE_DICT: utf8_bytes = c.encode('utf-8' ) parent = 0 for byte in utf8_bytes: key = (parent, byte) if key in self .hash_table: parent = self .hash_table[key] else : self ._add_node(parent, byte) def _add_node (self, parent, ch ): """内部方法:添加新节点(含FIFO替换)""" if self .next_code < MAX_SIZE: idx = self .next_code self .next_code += 1 else : idx = self .queue.popleft() old_parent, old_ch = self .dict_nodes[idx] del self .hash_table[(old_parent, old_ch)] self .dict_nodes[idx] = (parent, ch) self .hash_table[(parent, ch)] = idx self .queue.append(idx) return idx @staticmethod def _pack_bits (codes ): """将代码列表打包为位流字节""" bitbuf = 0 bits = 0 out = bytearray () for code in codes: bitbuf = (bitbuf << MAX_BITS) | code bits += MAX_BITS while bits >= 8 : bits -= 8 out.append((bitbuf >> bits) & 0xFF ) bitbuf &= (1 << bits) - 1 if bits > 0 : out.append((bitbuf << (8 - bits)) & 0xFF ) return bytes (out) @staticmethod def _unpack_bits (data ): """将位流字节解包为代码列表""" codes = [] bitbuf = 0 bits = 0 for byte in data: bitbuf = (bitbuf << 8 ) | byte bits += 8 while bits >= MAX_BITS: bits -= MAX_BITS codes.append((bitbuf >> bits) & ((1 << MAX_BITS) - 1 )) bitbuf &= (1 << bits) - 1 return codes def compress (self, data ): """压缩数据""" self .dict_init() codes = [] parent = 0 for byte in data: key = (parent, byte) if key in self .hash_table: parent = self .hash_table[key] else : codes.append(parent) self ._add_node(parent, byte) parent = self .hash_table[(0 , byte)] if parent != 0 : codes.append(parent) return self ._pack_bits(codes) def decompress (self, data ): """解压数据""" self .dict_init() codes = self ._unpack_bits(data) if not codes: return b'' out = [] prev_code = codes[0 ] current_str = self ._get_string(prev_code) out.append(current_str) first_ch = current_str[0 ] if current_str else 0 for code in codes[1 :]: if code == self .next_code: prev_str = self ._get_string(prev_code) current_str = prev_str + bytes ([first_ch]) else : current_str = self ._get_string(code) out.append(current_str) first_ch = current_str[0 ] if current_str else 0 self ._add_node(prev_code, first_ch) prev_code = code return b'' .join(out) def _get_string (self, code ): """根据代码获取对应的字符串""" stack = [] cur = code while cur != 0 : stack.append(self .dict_nodes[cur][1 ]) cur = self .dict_nodes[cur][0 ] stack.reverse() return bytes (stack) def main (): input_path = r"D:\tmp\TheCountofMonteCristo.txt" dir_path, filename = os.path.split(input_path) base_name = os.path.splitext(filename)[0 ] comp_path = os.path.join(dir_path, f"{base_name} .lzw" ) decomp_path = os.path.join(dir_path, f"{base_name} .dec" ) with open (input_path, 'rb' ) as f: in_data = f.read() in_len = len (in_data) lzw = LZW() t0 = time.time() comp_data = lzw.compress(in_data) t1 = time.time() with open (comp_path, 'wb' ) as f: f.write(comp_data) comp_len = len (comp_data) print (f"压缩完成: {in_len} -> {comp_len} bytes, 用时 {t1-t0:.3 f} s" ) lzw = LZW() t2 = time.time() decomp_data = lzw.decompress(comp_data) t3 = time.time() with open (decomp_path, 'wb' ) as f: f.write(decomp_data) decomp_len = len (decomp_data) print (f"解压完成: {decomp_len} bytes, 用时 {t3-t2:.3 f} s" ) if decomp_data == in_data: print ("校验通过" ) else : print ("校验失败!" ) if __name__ == "__main__" : main()
lzw.c
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 #include <stdio.h> #include <stdlib.h> #include <stdint.h> #include <string.h> #include <time.h> #include <ctype.h> #include <windows.h> #include <wchar.h> #include <locale.h> #define MAX_BITS 19 #define MAX_SIZE (1u << MAX_BITS) #define HASH_SIZE (1u << 20) typedef struct { int32_t parent; uint8_t ch; } Node; static void dict_init (void ) ;static int32_t add_node (int32_t parent, uint8_t ch) ;static void pack_bits (const int32_t *codes, size_t n, uint8_t **out_buf, size_t *out_len) ;static int32_t *unpack_bits (const uint8_t *data, size_t len, size_t *out_n) ;static void compress_file (const uint8_t *in, size_t in_len, uint8_t **out, size_t *out_len) ;static void decompress_file (const uint8_t *in, size_t in_len, uint8_t **out_buf, size_t *out_len) ;static uint8_t *read_file (const char *path, size_t *len) ;static void write_file (const char *path, const uint8_t *buf, size_t len) ;static Node dict[MAX_SIZE]; static int32_t hash_parent[HASH_SIZE]; static uint16_t hash_char[HASH_SIZE];static int32_t hash_val[HASH_SIZE]; static int32_t queue [MAX_SIZE]; static int32_t q_head = 0 , q_tail = 0 ; static int32_t next_code; static inline uint32_t hash_func (int32_t parent, uint8_t ch) { return ((uint32_t )parent * 131u + ch) & (HASH_SIZE - 1 ); } static void hash_clear (void ) { memset (hash_val, 0xFF , sizeof (hash_val)); } static int32_t hash_find (int32_t parent, uint8_t ch) { uint32_t pos = hash_func(parent, ch); while (hash_val[pos] != -1 ) { if (hash_parent[pos] == parent && hash_char[pos] == ch) return hash_val[pos]; pos = (pos + 1 ) & (HASH_SIZE - 1 ); } return -1 ; } static void hash_insert (int32_t parent, uint8_t ch, int32_t idx) { uint32_t pos = hash_func(parent, ch); while (hash_val[pos] != -1 ) pos = (pos + 1 ) & (HASH_SIZE - 1 ); hash_parent[pos] = parent; hash_char[pos] = ch; hash_val[pos] = idx; } static void dict_init (void ) { setlocale(LC_ALL, "" ); hash_clear(); dict[0 ].parent = -1 ; dict[0 ].ch = 0 ; next_code = 1 ; q_head = q_tail = 0 ; for (int i = 0 ; i < 256 ; ++i) { dict[next_code].parent = 0 ; dict[next_code].ch = (uint8_t )i; hash_insert(0 , (uint8_t )i, next_code); queue [q_tail++] = next_code; ++next_code; } const wchar_t *chinese_dict = L"的一是了我不人在他有这个上们来到时大地为子中你说生国年着就那和要她出也得里后自以会家可下而过天去能对小多然于心学么之都好看起发当没成只如事把还用第样道想作种开美总从无情己面最女但现前些所同日手又行意动\ 方期它头经长儿回位分爱老因很给名法间斯知世什两次使身者被高已亲其进此话常与活正感见明问力理尔点文几定本公特做外孩相西果走将月十实向声车全信重三机工物气每并别真打太新比才便夫再书部水像眼等体却加电主界门\ 利海受听表德少克代员许稜先口由死安写性马光白或住难望教命花结乐色更拉东神记处让母父应直字场平报友关放至张认接告入笑内英军候民岁往何度山觉路带万男边风解叫任金快原吃妈变通师立象数四失满战远格士音轻目条呢\ 病始达深完今提求清王化空业思切怎非找片罗钱紶吗语元喜曾离飞科言干流欢约各即指合反题必该论交终林请医晚制球决窢传画保读运及则房早院量苦火布品近坐产答星精视五连司巴奇管类未朋且婚台夜青北队久乎越观落尽形影\ 红爸百令周吧识步希亚术留市半热送兴造谈容极随演收首根讲整式取照办强石古华諣拿计您装似足双妻尼转诉米称丽客南领节衣站黑刻统断福城故历惊脸选包紧争另建维绝树系伤示愿持千史谁准联妇纪基买志静阿诗独复痛消社算\ 义竟确酒需单治卡幸兰念举仅钟怕共毛句息功官待究跟穿室易游程号居考突皮哪费倒价图具刚脑永歌响商礼细专黄块脚味灵改据般破引食仍存众注笔甚某沉血备习校默务土微娘须试怀料调广蜖苏显赛查密议底列富梦错座参八除跑" ; for (const wchar_t *p = chinese_dict; *p; ++p) { char utf8[4 ] = {0 }; int len = wctomb(utf8, *p); int32_t parent = 0 ; for (int i = 0 ; i < len; ++i) { int32_t nxt = hash_find(parent, (uint8_t )utf8[i]); if (nxt == -1 ) nxt = add_node(parent, (uint8_t )utf8[i]); parent = nxt; } } } static int32_t add_node (int32_t parent, uint8_t ch) { int32_t idx; if (next_code < MAX_SIZE) { idx = next_code++; } else { idx = queue [q_head]; q_head = (q_head + 1 ) % MAX_SIZE; int32_t op = dict[idx].parent; uint8_t oc = dict[idx].ch; uint32_t pos = hash_func(op, oc); while (!(hash_parent[pos] == op && hash_char[pos] == oc)) pos = (pos + 1 ) & (HASH_SIZE - 1 ); hash_val[pos] = -1 ; uint32_t nxt = (pos + 1 ) & (HASH_SIZE - 1 ); while (hash_val[nxt] != -1 ) { int32_t tp = hash_parent[nxt]; uint8_t tc = hash_char[nxt]; int32_t tv = hash_val[nxt]; hash_val[nxt] = -1 ; hash_insert(tp, tc, tv); nxt = (nxt + 1 ) & (HASH_SIZE - 1 ); } } dict[idx].parent = parent; dict[idx].ch = ch; hash_insert(parent, ch, idx); queue [q_tail] = idx; q_tail = (q_tail + 1 ) % MAX_SIZE; return idx; } static void pack_bits (const int32_t *codes, size_t n, uint8_t **out_buf, size_t *out_len) { uint32_t bitbuf = 0 ; int bits = 0 ; size_t cap = n * (MAX_BITS + 7 ) / 8 + 4 ; uint8_t *out = (uint8_t *)malloc (cap); size_t len = 0 ; for (size_t i = 0 ; i < n; ++i) { bitbuf = (bitbuf << MAX_BITS) | (uint32_t )codes[i]; bits += MAX_BITS; while (bits >= 8 ) { bits -= 8 ; out[len++] = (bitbuf >> bits) & 0xFF ; } } if (bits) { out[len++] = (bitbuf << (8 - bits)) & 0xFF ; } *out_buf = out; *out_len = len; } static int32_t *unpack_bits (const uint8_t *data, size_t len, size_t *out_n) { size_t cap = len * 8 / MAX_BITS + 4 ; int32_t *codes = (int32_t *)malloc (cap * sizeof (int32_t )); size_t n = 0 ; uint32_t bitbuf = 0 ; int bits = 0 ; for (size_t i = 0 ; i < len; ++i) { bitbuf = (bitbuf << 8 ) | data[i]; bits += 8 ; while (bits >= MAX_BITS) { bits -= MAX_BITS; codes[n++] = (bitbuf >> bits) & ((1u << MAX_BITS) - 1 ); } } *out_n = n; return codes; } static void compress_file (const uint8_t *in, size_t in_len, uint8_t **out, size_t *out_len) { int32_t *codes = (int32_t *)malloc ((in_len + 1 ) * sizeof (int32_t )); size_t n_codes = 0 ; int32_t parent = 0 ; for (size_t i = 0 ; i < in_len; ++i) { uint8_t c = in[i]; int32_t nxt = hash_find(parent, c); if (nxt != -1 ) { parent = nxt; } else { codes[n_codes++] = parent; add_node(parent, c); parent = hash_find(0 , c); } } if (parent != 0 ) codes[n_codes++] = parent; pack_bits(codes, n_codes, out, out_len); free (codes); } static void decompress_file (const uint8_t *in, size_t in_len, uint8_t **out_buf, size_t *out_len) { size_t n_codes; int32_t *codes = unpack_bits(in, in_len, &n_codes); size_t cap = 4096 ; uint8_t *out = (uint8_t *)malloc (cap); size_t len = 0 ; int32_t prev_code = 0 ; uint8_t first_ch = 0 ; static uint8_t stack [MAX_SIZE]; int top; for (size_t i = 0 ; i < n_codes; ++i) { int32_t code = codes[i]; top = 0 ; int32_t cur = code; if (code == next_code && prev_code != 0 ) { cur = prev_code; stack [top++] = first_ch; } while (cur != 0 ) { stack [top++] = dict[cur].ch; cur = dict[cur].parent; } first_ch = stack [top - 1 ]; if (len + (size_t )top > cap) { do { cap <<= 1 ; } while (len + (size_t )top > cap); out = (uint8_t *)realloc (out, cap); } for (int j = top - 1 ; j >= 0 ; --j) out[len++] = stack [j]; if (prev_code != 0 ) { add_node(prev_code, first_ch); } prev_code = code; } free (codes); *out_buf = out; *out_len = len; } static uint8_t *read_file (const char *path, size_t *len) { FILE *fp = fopen(path, "rb" ); if (!fp) { perror(path); exit (1 ); } fseek(fp, 0 , SEEK_END); *len = ftell(fp); fseek(fp, 0 , SEEK_SET); uint8_t *buf = (uint8_t *)malloc (*len); fread(buf, 1 , *len, fp); fclose(fp); return buf; } static void write_file (const char *path, const uint8_t *buf, size_t len) { FILE *fp = fopen(path, "wb" ); if (!fp) { perror(path); exit (1 ); } fwrite(buf, 1 , len, fp); fclose(fp); } int main (int argc, char *argv[]) { const char *input_path; char *comp_path, *decomp_path; char *filename, *dir_path, *last_sep, *dot_pos; SetConsoleOutputCP(CP_UTF8); if (argc >= 2 ) { input_path = argv[1 ]; } else { fprintf (stderr , "用法: %s <输入文件路径>\n" , argv[0 ]); return 1 ; } last_sep = strrchr (input_path, '/' ); if (!last_sep) last_sep = strrchr (input_path, '\\' ); if (last_sep) { size_t dir_len = last_sep - input_path + 1 ; dir_path = (char *)malloc (dir_len); strncpy (dir_path, input_path, dir_len); filename = last_sep + 1 ; } else { dir_path = (char *)"." ; filename = (char *)input_path; } dot_pos = strrchr (filename, '.' ); if (dot_pos) { size_t base_len = dot_pos - filename; char *base_filename = (char *)malloc (base_len + 1 ); strncpy (base_filename, filename, base_len); base_filename[base_len] = '\0' ; filename = base_filename; } size_t fn_len = strlen (filename); comp_path = (char *)malloc (strlen (dir_path) + fn_len + 5 ); decomp_path = (char *)malloc (strlen (dir_path) + fn_len + 5 ); snprintf (comp_path, strlen (dir_path) + fn_len + 5 , "%s%s.lzw" , dir_path, filename); snprintf (decomp_path, strlen (dir_path) + fn_len + 5 , "%s%s.dec" , dir_path, filename); size_t in_len; uint8_t *in_buf = read_file(input_path, &in_len); dict_init(); clock_t t0 = clock(); uint8_t *comp_buf; size_t comp_len; compress_file(in_buf, in_len, &comp_buf, &comp_len); clock_t t1 = clock(); write_file(comp_path, comp_buf, comp_len); printf ("压缩完成: %zu -> %zu bytes, 用时 %.3f s\n" , in_len, comp_len, (double )(t1 - t0) / CLOCKS_PER_SEC); dict_init(); clock_t t2 = clock(); uint8_t *decomp_buf; size_t decomp_len; decompress_file(comp_buf, comp_len, &decomp_buf, &decomp_len); clock_t t3 = clock(); write_file(decomp_path, decomp_buf, decomp_len); printf ("解压完成: %zu bytes, 用时 %.3f s\n" , decomp_len, (double )(t3 - t2) / CLOCKS_PER_SEC); if (decomp_len != in_len || memcmp (in_buf, decomp_buf, in_len) != 0 ) { fprintf (stderr , "校验失败!\n" ); return 1 ; } puts ("校验通过" ); free (in_buf); free (comp_buf); free (decomp_buf); free (dir_path); free (comp_path); free (decomp_path); if (dot_pos) free (filename); return 0 ; }
lzw.java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 import java.io.*;import java.nio.file.Files;import java.nio.file.Paths;import java.util.*;public class LZW { private static final int MAX_BITS = 19 ; private static final int MAX_SIZE = 1 << MAX_BITS; private static final int HASH_SIZE = 1 << 20 ; private static final String CHINESE_DICT = "的一是了我不人在他有这个上们来到时大地为子中你说生国年着就那和要她出也得里后自以会家可下而过天去能对小多然于心学么之都好看起发当没成只如事把还用第样道想作种开美总从无情己面最女但现前些所同日手又行意动" + "方期它头经长儿回位分爱老因很给名法间斯知世什两次使身者被高已亲其进此话常与活正感见明问力理尔点文几定本公特做外孩相西果走将月十实向声车全信重三机工物气每并别真打太新比才便夫再书部水像眼等体却加电主界门" + "利海受听表德少克代员许稜先口由死安写性马光白或住难望教命花结乐色更拉东神记处让母父应直字场平报友关放至张认接告入笑内英军候民岁往何度山觉路带万男边风解叫任金快原吃妈变通师立象数四失满战远格士音轻目条呢" + "病始达深完今提求清王化空业思切怎非找片罗钱紶吗语元喜曾离飞科言干流欢约各即指合反题必该论交终林请医晚制球决窢传画保读运及则房早院量苦火布品近坐产答星精视五连司巴奇管类未朋且婚台夜青北队久乎越观落尽形影" + "红爸百令周吧识步希亚术留市半热送兴造谈容极随演收首根讲整式取照办强石古华諣拿计您装似足双妻尼转诉米称丽客南领节衣站黑刻统断福城故历惊脸选包紧争另建维绝树系伤示愿持千史谁准联妇纪基买志静阿诗独复痛消社算" + "义竟确酒需单治卡幸兰念举仅钟怕共毛句息功官待究跟穿室易游程号居考突皮哪费倒价图具刚脑永歌响商礼细专黄块脚味灵改据般破引食仍存众注笔甚某沉血备习校默务土微娘须试怀料调广蜖苏显赛查密议底列富梦错座参八除跑" ; private final int [] dictParent = new int [MAX_SIZE]; private final byte [] dictChar = new byte [MAX_SIZE]; private final int [] hashParent = new int [HASH_SIZE]; private final byte [] hashChar = new byte [HASH_SIZE]; private final int [] hashVal = new int [HASH_SIZE]; private final int [] queue = new int [MAX_SIZE]; private int qHead = 0 , qTail = 0 ; private int nextCode; private void dictInit () { Arrays.fill(hashVal, -1 ); Arrays.fill(dictParent, -1 ); Arrays.fill(dictChar, (byte )0 ); dictParent[0 ] = -1 ; dictChar[0 ] = 0 ; nextCode = 1 ; qHead = qTail = 0 ; for (int i = 0 ; i < 256 ; i++) { dictParent[nextCode] = 0 ; dictChar[nextCode] = (byte )i; hashInsert(0 , (byte )i, nextCode); queue[qTail++] = nextCode; nextCode++; } try { for (char c : CHINESE_DICT.toCharArray()) { byte [] utf8 = String.valueOf(c).getBytes("UTF-8" ); int parent = 0 ; for (byte b : utf8) { int next = hashFind(parent, b); if (next == -1 ) { next = addNode(parent, b); } parent = next; } } } catch (UnsupportedEncodingException e) { System.err.println("UTF-8编码不支持" ); } } private int hashFunc (int parent, byte ch) { return ((parent * 131 + (ch & 0xFF )) & (HASH_SIZE - 1 )); } private int hashFind (int parent, byte ch) { int pos = hashFunc(parent, ch); while (hashVal[pos] != -1 ) { if (hashParent[pos] == parent && hashChar[pos] == ch) { return hashVal[pos]; } pos = (pos + 1 ) & (HASH_SIZE - 1 ); } return -1 ; } private void hashInsert (int parent, byte ch, int idx) { int pos = hashFunc(parent, ch); while (hashVal[pos] != -1 ) { pos = (pos + 1 ) & (HASH_SIZE - 1 ); } hashParent[pos] = parent; hashChar[pos] = ch; hashVal[pos] = idx; } private int addNode (int parent, byte ch) { int idx; if (nextCode < MAX_SIZE) { idx = nextCode++; } else { idx = queue[qHead]; qHead = (qHead + 1 ) % MAX_SIZE; int oldParent = dictParent[idx]; byte oldCh = dictChar[idx]; int pos = hashFunc(oldParent, oldCh); while (!(hashParent[pos] == oldParent && hashChar[pos] == oldCh)) { pos = (pos + 1 ) & (HASH_SIZE - 1 ); } hashVal[pos] = -1 ; int nextPos = (pos + 1 ) & (HASH_SIZE - 1 ); while (hashVal[nextPos] != -1 ) { int tp = hashParent[nextPos]; byte tc = hashChar[nextPos]; int tv = hashVal[nextPos]; hashVal[nextPos] = -1 ; hashInsert(tp, tc, tv); nextPos = (nextPos + 1 ) & (HASH_SIZE - 1 ); } } dictParent[idx] = parent; dictChar[idx] = ch; hashInsert(parent, ch, idx); queue[qTail] = idx; qTail = (qTail + 1 ) % MAX_SIZE; return idx; } private byte [] packBits(int [] codes) { ByteArrayOutputStream out = new ByteArrayOutputStream (codes.length * 3 ); int bitBuf = 0 ; int bits = 0 ; for (int code : codes) { bitBuf = (bitBuf << MAX_BITS) | (code & ((1 << MAX_BITS) - 1 )); bits += MAX_BITS; while (bits >= 8 ) { bits -= 8 ; out.write((bitBuf >> bits) & 0xFF ); } } if (bits > 0 ) { out.write((bitBuf << (8 - bits)) & 0xFF ); } return out.toByteArray(); } private int [] unpackBits(byte [] data) { int [] codes = new int [data.length * 8 / MAX_BITS + 1 ]; int codeCount = 0 ; int bitBuf = 0 ; int bits = 0 ; for (byte b : data) { bitBuf = (bitBuf << 8 ) | (b & 0xFF ); bits += 8 ; while (bits >= MAX_BITS) { bits -= MAX_BITS; codes[codeCount++] = (bitBuf >> bits) & ((1 << MAX_BITS) - 1 ); } } return Arrays.copyOf(codes, codeCount); } public byte [] compress(byte [] input) { int [] codes = new int [input.length]; int codeCount = 0 ; int parent = 0 ; for (byte c : input) { int next = hashFind(parent, c); if (next != -1 ) { parent = next; } else { codes[codeCount++] = parent; addNode(parent, c); parent = hashFind(0 , c); } } if (parent != 0 ) { codes[codeCount++] = parent; } return packBits(Arrays.copyOf(codes, codeCount)); } public byte [] decompress(byte [] input) { int [] codes = unpackBits(input); ByteArrayOutputStream out = new ByteArrayOutputStream (input.length * 2 ); int prevCode = 0 ; byte firstCh = 0 ; byte [] stack = new byte [MAX_SIZE]; for (int code : codes) { int top = 0 ; int cur = code; if (code == nextCode && prevCode != 0 ) { cur = prevCode; stack[top++] = firstCh; } while (cur != 0 ) { stack[top++] = dictChar[cur]; cur = dictParent[cur]; } firstCh = stack[top - 1 ]; for (int j = top - 1 ; j >= 0 ; j--) { out.write(stack[j]); } if (prevCode != 0 ) { addNode(prevCode, firstCh); } prevCode = code; } return out.toByteArray(); } private static byte [] readFile(String path) throws IOException { return Files.readAllBytes(Paths.get(path)); } private static void writeFile (String path, byte [] data) throws IOException { Files.write(Paths.get(path), data); } public static void main (String[] args) throws IOException { String inputPath; if (args.length == 0 ) { inputPath = "D:\\test\\Twilight.txt" ; System.out.println("未指定输入路径,使用默认路径: " + inputPath); } else if (args.length == 1 ) { inputPath = args[0 ]; } else { System.err.println("错误:参数过多,用法: java LZW [输入文件路径]" ); return ; } String baseName = new File (inputPath).getName().replaceFirst("[.][^.]+$" , "" ); String compPath = baseName + ".lzw" ; String decompPath = baseName + ".dec" ; LZW compressor = new LZW (); compressor.dictInit(); byte [] input = readFile(inputPath); long start = System.currentTimeMillis(); byte [] compressed = compressor.compress(input); long compressTime = System.currentTimeMillis() - start; writeFile(compPath, compressed); System.out.printf("压缩完成: %d -> %d bytes, 用时 %.3fs\n" , input.length, compressed.length, compressTime / 1000.0 ); compressor = new LZW (); compressor.dictInit(); start = System.currentTimeMillis(); byte [] decompressed = compressor.decompress(compressed); long decompressTime = System.currentTimeMillis() - start; writeFile(decompPath, decompressed); System.out.printf("解压完成: %d bytes, 用时 %.3fs\n" , decompressed.length, decompressTime / 1000.0 ); if (Arrays.equals(input, decompressed)) { System.out.println("校验通过" ); } else { System.out.println("校验失败!" ); } } }
lzw.js
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 const fs = require ('fs' );class LZW { static MAX_BITS = 19 ; static MAX_SIZE = 1 << LZW .MAX_BITS ; static HASH_SIZE = 1 << 20 ; static CHINESE_DICT = "的一是了我不人在他有这个上们来到时大地为子中你说生国年着就那和要她出也得里后自以会家可下而过天去能对小多然于心学么之都好看起发当没成只如事把还用第样道想作种开美总从无情己面最女但现前些所同日手又行意动" + "方期它头经长儿回位分爱老因很给名法间斯知世什两次使身者被高已亲其进此话常与活正感见明问力理尔点文几定本公特做外孩相西果走将月十实向声车全信重三机工物气每并别真打太新比才便夫再书部水像眼等体却加电主界门" + "利海受听表德少克代员许稜先口由死安写性马光白或住难望教命花结乐色更拉东神记处让母父应直字场平报友关放至张认接告入笑内英军候民岁往何度山觉路带万男边风解叫任金快原吃妈变通师立象数四失满战远格士音轻目条呢" + "病始达深完今提求清王化空业思切怎非找片罗钱紶吗语元喜曾离飞科言干流欢约各即指合反题必该论交终林请医晚制球决窢传画保读运及则房早院量苦火布品近坐产答星精视五连司巴奇管类未朋且婚台夜青北队久乎越观落尽形影" + "红爸百令周吧识步希亚术留市半热送兴造谈容极随演收首根讲整式取照办强石古华諣拿计您装似足双妻尼转诉米称丽客南领节衣站黑刻统断福城故历惊脸选包紧争另建维绝树系伤示愿持千史谁准联妇纪基买志静阿诗独复痛消社算" + "义竟确酒需单治卡幸兰念举仅钟怕共毛句息功官待究跟穿室易游程号居考突皮哪费倒价图具刚脑永歌响商礼细专黄块脚味灵改据般破引食仍存众注笔甚某沉血备习校默务土微娘须试怀料调广蜖苏显赛查密议底列富梦错座参八除跑" ; constructor ( this .dictParent = new Int32Array (LZW .MAX_SIZE ); this .dictChar = new Uint8Array (LZW .MAX_SIZE ); this .hashParent = new Int32Array (LZW .HASH_SIZE ); this .hashChar = new Uint8Array (LZW .HASH_SIZE ); this .hashVal = new Int32Array (LZW .HASH_SIZE ); this .queue = new Int32Array (LZW .MAX_SIZE ); this .qHead = 0 ; this .qTail = 0 ; this .nextCode = 0 ; } dictInit ( this .hashVal .fill (-1 ); this .dictParent .fill (-1 ); this .dictChar .fill (0 ); this .dictParent [0 ] = -1 ; this .dictChar [0 ] = 0 ; this .nextCode = 1 ; this .qHead = this .qTail = 0 ; for (let i = 0 ; i < 256 ; i++) { this .dictParent [this .nextCode ] = 0 ; this .dictChar [this .nextCode ] = i; this .hashInsert (0 , i, this .nextCode ); this .queue [this .qTail ++] = this .nextCode ; this .nextCode ++; } for (const c of LZW .CHINESE_DICT ) { const utf8 = new TextEncoder ().encode (c); let parent = 0 ; for (const b of utf8) { let next = this .hashFind (parent, b); if (next === -1 ) { next = this .addNode (parent, b); } parent = next; } } } hashFunc (parent, ch ) { return ((parent * 131 + ch) & (LZW .HASH_SIZE - 1 )); } hashFind (parent, ch ) { let pos = this .hashFunc (parent, ch); while (this .hashVal [pos] !== -1 ) { if (this .hashParent [pos] === parent && this .hashChar [pos] === ch) { return this .hashVal [pos]; } pos = (pos + 1 ) & (LZW .HASH_SIZE - 1 ); } return -1 ; } hashInsert (parent, ch, idx ) { let pos = this .hashFunc (parent, ch); while (this .hashVal [pos] !== -1 ) { pos = (pos + 1 ) & (LZW .HASH_SIZE - 1 ); } this .hashParent [pos] = parent; this .hashChar [pos] = ch; this .hashVal [pos] = idx; } addNode (parent, ch ) { let idx; if (this .nextCode < LZW .MAX_SIZE ) { idx = this .nextCode ++; } else { idx = this .queue [this .qHead ]; this .qHead = (this .qHead + 1 ) % LZW .MAX_SIZE ; const oldParent = this .dictParent [idx]; const oldCh = this .dictChar [idx]; let pos = this .hashFunc (oldParent, oldCh); while (!(this .hashParent [pos] === oldParent && this .hashChar [pos] === oldCh)) { pos = (pos + 1 ) & (LZW .HASH_SIZE - 1 ); } this .hashVal [pos] = -1 ; let nextPos = (pos + 1 ) & (LZW .HASH_SIZE - 1 ); while (this .hashVal [nextPos] !== -1 ) { const tp = this .hashParent [nextPos]; const tc = this .hashChar [nextPos]; const tv = this .hashVal [nextPos]; this .hashVal [nextPos] = -1 ; this .hashInsert (tp, tc, tv); nextPos = (nextPos + 1 ) & (LZW .HASH_SIZE - 1 ); } } this .dictParent [idx] = parent; this .dictChar [idx] = ch; this .hashInsert (parent, ch, idx); this .queue [this .qTail ] = idx; this .qTail = (this .qTail + 1 ) % LZW .MAX_SIZE ; return idx; } packBits (codes ) { const out = new Uint8Array (codes.length * 3 ); let outPos = 0 ; let bitBuf = 0 ; let bits = 0 ; for (const code of codes) { bitBuf = (bitBuf << LZW .MAX_BITS ) | (code & ((1 << LZW .MAX_BITS ) - 1 )); bits += LZW .MAX_BITS ; while (bits >= 8 ) { bits -= 8 ; out[outPos++] = (bitBuf >> bits) & 0xFF ; } } if (bits > 0 ) { out[outPos++] = (bitBuf << (8 - bits)) & 0xFF ; } return out.slice (0 , outPos); } unpackBits (data ) { const codes = new Int32Array (data.length * 8 / LZW .MAX_BITS + 1 ); let codeCount = 0 ; let bitBuf = 0 ; let bits = 0 ; for (const byte of data) { bitBuf = (bitBuf << 8 ) | byte; bits += 8 ; while (bits >= LZW .MAX_BITS ) { bits -= LZW .MAX_BITS ; codes[codeCount++] = (bitBuf >> bits) & ((1 << LZW .MAX_BITS ) - 1 ); } } if (bits >= LZW .MAX_BITS ) { codes[codeCount++] = (bitBuf >> (bits - LZW .MAX_BITS )) & ((1 << LZW .MAX_BITS ) - 1 ); } return codes.slice (0 , codeCount);} compress (input ) { const codes = new Int32Array (input.length ); let codeCount = 0 ; let parent = 0 ; for (const byte of input) { const next = this .hashFind (parent, byte); if (next !== -1 ) { parent = next; } else { codes[codeCount++] = parent; this .addNode (parent, byte); parent = this .hashFind (0 , byte); } } if (parent !== 0 ) { codes[codeCount++] = parent; } return this .packBits (codes.slice (0 , codeCount));} decompress (input ) { const codes = this .unpackBits (input); const out = new Uint8Array (input.length * 4 ); let outPos = 0 ; let prevCode = 0 ; let firstCh = 0 ; const stack = new Uint8Array (LZW .MAX_SIZE ); for (const code of codes) { let top = 0 ; let cur = code; if (code === this .nextCode && prevCode !== 0 ) { cur = prevCode; stack[top++] = firstCh; } else if (code > this .nextCode ) { throw new Error ('无效的压缩数据' ); } while (cur !== 0 ) { stack[top++] = this .dictChar [cur]; cur = this .dictParent [cur]; } firstCh = stack[top - 1 ]; for (let j = top - 1 ; j >= 0 ; j--) { out[outPos++] = stack[j]; } if (prevCode !== 0 && this .nextCode < LZW .MAX_SIZE ) { this .addNode (prevCode, firstCh); } prevCode = code; } return out.slice (0 , outPos); } } async function main ( try { const inputPath = process.argv [2 ] || 'Twilight.txt' ; const input = await fs.promises .readFile (inputPath); const baseName = inputPath.replace (/\.[^/.]+$/ , '' ); const compPath = baseName + '.lzw' ; const decompPath = baseName + '.dec' ; const compressor = new LZW (); compressor.dictInit (); const startCompress = performance.now (); const compressed = compressor.compress (input); const compressTime = performance.now () - startCompress; await fs.promises .writeFile (compPath, compressed); console .log (`压缩完成: ${input.length} -> ${compressed.length} bytes, 用时 ${(compressTime/1000 ).toFixed(3 )} s` ); const decompressor = new LZW (); decompressor.dictInit (); const startDecompress = performance.now (); const decompressed = decompressor.decompress (compressed); const decompressTime = performance.now () - startDecompress; await fs.promises .writeFile (decompPath, decompressed); console .log (`解压完成: ${decompressed.length} bytes, 用时 ${(decompressTime/1000 ).toFixed(3 )} s` ); if (input.length !== decompressed.length ) { console .log (`长度不匹配: 原始=${input.length} , 解压=${decompressed.length} ` ); } let diffCount = 0 ;for (let i = 0 ; i < Math .min (input.length , decompressed.length ); i++) { if (input[i] !== decompressed[i]) { diffCount++; if (diffCount <= 10 ) { console .log (`位置 ${i} : 原始=${input[i]} , 解压=${decompressed[i]} ` ); } } } if (diffCount > 0 ) { console .log (`共发现 ${diffCount} 处差异` ); } else { console .log ('校验通过' ); } } catch (error) { console .error ('错误:' , error.message ); } } if (require .main === module ) { main (); } module .exports = LZW ;
lzw.go
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 package mainimport ( "flag" "fmt" "os" "path/filepath" "strings" "time" ) const ( MAX_BITS = 19 MAX_SIZE = 1 << MAX_BITS HASH_SIZE = 1 << 20 ) var CHINESE_DICT = "的一是了我不人在他有这个上们来到时大地为子中你说生国年着就那和要她出也得里后自以会家可下而过天去能对小多然于心学么之都好看起发当没成只如事把还用第样道想作种开美总从无情己面最女但现前些所同日手又行意动" +"方期它头经长儿回位分爱老因很给名法间斯知世什两次使身者被高已亲其进此话常与活正感见明问力理尔点文几定本公特做外孩相西果走将月十实向声车全信重三机工物气每并别真打太新比才便夫再书部水像眼等体却加电主界门" +"利海受听表德少克代员许稜先口由死安写性马光白或住难望教命花结乐色更拉东神记处让母父应直字场平报友关放至张认接告入笑内英军候民岁往何度山觉路带万男边风解叫任金快原吃妈变通师立象数四失满战远格士音轻目条呢" +"病始达深完今提求清王化空业思切怎非找片罗钱紶吗语元喜曾离飞科言干流欢约各即指合反题必该论交终林请医晚制球决窢传画保读运及则房早院量苦火布品近坐产答星精视五连司巴奇管类未朋且婚台夜青北队久乎越观落尽形影" +"红爸百令周吧识步希亚术留市半热送兴造谈容极随演收首根讲整式取照办强石古华諣拿计您装似足双妻尼转诉米称丽客南领节衣站黑刻统断福城故历惊脸选包紧争另建维绝树系伤示愿持千史谁准联妇纪基买志静阿诗独复痛消社算" +"义竟确酒需单治卡幸兰念举仅钟怕共毛句息功官待究跟穿室易游程号居考突皮哪费倒价图具刚脑永歌响商礼细专黄块脚味灵改据般破引食仍存众注笔甚某沉血备习校默务土微娘须试怀料调广蜖苏显赛查密议底列富梦错座参八除跑" type LZW struct { dictParent []int32 dictChar []uint8 hashParent []int32 hashChar []uint8 hashVal []int32 queue []int32 qHead int32 qTail int32 nextCode int32 } func NewLZW () return &LZW{ dictParent: make ([]int32 , MAX_SIZE), dictChar: make ([]uint8 , MAX_SIZE), hashParent: make ([]int32 , HASH_SIZE), hashChar: make ([]uint8 , HASH_SIZE), hashVal: make ([]int32 , HASH_SIZE), queue: make ([]int32 , MAX_SIZE), } } func (lzw *LZW) for i := range lzw.hashVal { lzw.hashVal[i] = -1 } for i := range lzw.dictParent { lzw.dictParent[i] = -1 } lzw.dictParent[0 ] = -1 lzw.dictChar[0 ] = 0 lzw.nextCode = 1 lzw.qHead = 0 lzw.qTail = 0 for i := 0 ; i < 256 ; i++ { lzw.dictParent[lzw.nextCode] = 0 lzw.dictChar[lzw.nextCode] = uint8 (i) lzw.hashInsert(0 , uint8 (i), lzw.nextCode) lzw.queue[lzw.qTail] = lzw.nextCode lzw.qTail = (lzw.qTail + 1 ) % MAX_SIZE lzw.nextCode++ } for _, c := range CHINESE_DICT { utf8 := []byte (string (c)) parent := int32 (0 ) for _, b := range utf8 { next := lzw.hashFind(parent, b) if next == -1 { next = lzw.addNode(parent, b) } parent = next } } } func (lzw *LZW) int32 , ch uint8 ) uint32 { return uint32 ((uint32 (parent)*131 + uint32 (ch)) & (HASH_SIZE - 1 )) } func (lzw *LZW) int32 , ch uint8 ) int32 { pos := lzw.hashFunc(parent, ch) for lzw.hashVal[pos] != -1 { if lzw.hashParent[pos] == parent && lzw.hashChar[pos] == ch { return lzw.hashVal[pos] } pos = (pos + 1 ) & (HASH_SIZE - 1 ) } return -1 } func (lzw *LZW) int32 , ch uint8 , idx int32 ) { pos := lzw.hashFunc(parent, ch) for lzw.hashVal[pos] != -1 { pos = (pos + 1 ) & (HASH_SIZE - 1 ) } lzw.hashParent[pos] = parent lzw.hashChar[pos] = ch lzw.hashVal[pos] = idx } func (lzw *LZW) int32 , ch uint8 ) int32 { var idx int32 if lzw.nextCode < MAX_SIZE { idx = lzw.nextCode lzw.nextCode++ } else { idx = lzw.queue[lzw.qHead] lzw.qHead = (lzw.qHead + 1 ) % MAX_SIZE oldParent := lzw.dictParent[idx] oldCh := lzw.dictChar[idx] pos := lzw.hashFunc(oldParent, oldCh) for !(lzw.hashParent[pos] == oldParent && lzw.hashChar[pos] == oldCh) { pos = (pos + 1 ) & (HASH_SIZE - 1 ) } lzw.hashVal[pos] = -1 nextPos := (pos + 1 ) & (HASH_SIZE - 1 ) for lzw.hashVal[nextPos] != -1 { tp := lzw.hashParent[nextPos] tc := lzw.hashChar[nextPos] tv := lzw.hashVal[nextPos] lzw.hashVal[nextPos] = -1 lzw.hashInsert(tp, tc, tv) nextPos = (nextPos + 1 ) & (HASH_SIZE - 1 ) } } lzw.dictParent[idx] = parent lzw.dictChar[idx] = ch lzw.hashInsert(parent, ch, idx) lzw.queue[lzw.qTail] = idx lzw.qTail = (lzw.qTail + 1 ) % MAX_SIZE return idx } func (lzw *LZW) int32 ) []uint8 { out := make ([]uint8 , len (codes)*3 ) outPos := 0 var bitBuf uint32 bits := 0 for _, code := range codes { bitBuf = (bitBuf << MAX_BITS) | uint32 (code&((1 <<MAX_BITS)-1 )) bits += MAX_BITS for bits >= 8 { bits -= 8 out[outPos] = uint8 ((bitBuf >> bits) & 0xFF ) outPos++ } } if bits > 0 { out[outPos] = uint8 ((bitBuf << (8 - bits)) & 0xFF ) outPos++ } return out[:outPos] } func (lzw *LZW) uint8 ) []int32 { codes := make ([]int32 , len (data)*8 /MAX_BITS+1 ) codeCount := 0 var bitBuf uint32 bits := 0 for _, b := range data { bitBuf = (bitBuf << 8 ) | uint32 (b) bits += 8 for bits >= MAX_BITS { bits -= MAX_BITS codes[codeCount] = int32 ((bitBuf >> bits) & ((1 << MAX_BITS) - 1 )) codeCount++ } } if bits >= MAX_BITS { codes[codeCount] = int32 ((bitBuf >> (bits - MAX_BITS)) & ((1 << MAX_BITS) - 1 )) codeCount++ } return codes[:codeCount] } func (lzw *LZW) uint8 ) []uint8 { codes := make ([]int32 , len (input)) codeCount := 0 parent := int32 (0 ) for _, b := range input { next := lzw.hashFind(parent, b) if next != -1 { parent = next } else { codes[codeCount] = parent codeCount++ lzw.addNode(parent, b) parent = lzw.hashFind(0 , b) } } if parent != 0 { codes[codeCount] = parent codeCount++ } return lzw.packBits(codes[:codeCount]) } func (lzw *LZW) uint8 ) []uint8 { codes := lzw.unpackBits(input) out := make ([]uint8 , len (input)*4 ) outPos := 0 var prevCode int32 var firstCh uint8 stack := make ([]uint8 , MAX_SIZE) for _, code := range codes { top := 0 cur := code if code == lzw.nextCode && prevCode != 0 { cur = prevCode stack[top] = firstCh top++ } else if code > lzw.nextCode { panic ("无效的压缩数据" ) } for cur != 0 { stack[top] = lzw.dictChar[cur] top++ cur = lzw.dictParent[cur] } firstCh = stack[top-1 ] for j := top - 1 ; j >= 0 ; j-- { out[outPos] = stack[j] outPos++ } if prevCode != 0 && lzw.nextCode < MAX_SIZE { lzw.addNode(prevCode, firstCh) } prevCode = code } return out[:outPos] } func main () fmt.Println("------------------------------------\n 示例:lzw.exe -input 您的文件路径,未提供 -input 参数,使用默认 Twilight.txt\n------------------------------------" ) inputPath := flag.String("input" , "Twilight.txt" , "输入文件路径" ) flag.Parse() input, err := os.ReadFile(*inputPath) if err != nil { fmt.Printf("读取文件失败: %v\n" , err) return } baseName := strings.TrimSuffix(*inputPath, filepath.Ext(*inputPath)) compPath := baseName + ".lzw" decompPath := baseName + ".dec" compressor := NewLZW() compressor.dictInit() startCompress := time.Now() compressed := compressor.compress(input) compressTime := time.Since(startCompress) if err := os.WriteFile(compPath, compressed, 0644 ); err != nil { fmt.Printf("写入压缩文件失败: %v\n" , err) return } fmt.Printf("压缩完成: %d -> %d bytes, 用时 %.3fs, 文件保存路径 %s\n" , len (input), len (compressed), compressTime.Seconds(), compPath) decompressor := NewLZW() decompressor.dictInit() startDecompress := time.Now() decompressed := decompressor.decompress(compressed) decompressTime := time.Since(startDecompress) if err := os.WriteFile(decompPath, decompressed, 0644 ); err != nil { fmt.Printf("写入解压文件失败: %v\n" , err) return } fmt.Printf("解压完成: %d bytes, 用时 %.3fs\n" , len (decompressed), decompressTime.Seconds()) if len (input) != len (decompressed) { fmt.Printf("长度不匹配: 原始=%d, 解压=%d\n" , len (input), len (decompressed)) } diffCount := 0 for i := 0 ; i < len (input) && i < len (decompressed); i++ { if input[i] != decompressed[i] { diffCount++ if diffCount <= 10 { fmt.Printf("位置 %d: 原始=%d, 解压=%d\n" , i, input[i], decompressed[i]) } } } if diffCount > 0 { fmt.Printf("共发现 %d 处差异\n" , diffCount) } else { fmt.Println("校验通过" ) } }
lzw.m
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 classdef LZW < handle properties (Constant) MAX_BITS = 19 ; MAX_SIZE = 2 ^LZW.MAX_BITS; HASH_SIZE = 2 ^20 ; CHINESE_DICT = ['的一是了我不人在他有这个上们来到时大地为子中你说生国年着就那和要她出也得里后自以会家可下而过天去能对小多然于心学么之都好看起发当没成只如事把还用第样道想作种开美总从无情己面最女但现前些所同日手又行意动' ... '方期它头经长儿回位分爱老因很给名法间斯知世什两次使身者被高已亲其进此话常与活正感见明问力理尔点文几定本公特做外孩相西果走将月十实向声车全信重三机工物气每并别真打太新比才便夫再书部水像眼等体却加电主界门' ... '利海受听表德少克代员许稜先口由死安写性马光白或住难望教命花结乐色更拉东神记处让母父应直字场平报友关放至张认接告入笑内英军候民岁往何度山觉路带万男边风解叫任金快原吃妈变通师立象数四失满战远格士音轻目条呢' ... '病始达深完今提求清王化空业思切怎非找片罗钱紶吗语元喜曾离飞科言干流欢约各即指合反题必该论交终林请医晚制球决窢传画保读运及则房早院量苦火布品近坐产答星精视五连司巴奇管类未朋且婚台夜青北队久乎越观落尽形影' ... '红爸百令周吧识步希亚术留市半热送兴造谈容极随演收首根讲整式取照办强石古华諣拿计您装似足双妻尼转诉米称丽客南领节衣站黑刻统断福城故历惊脸选包紧争另建维绝树系伤示愿持千史谁准联妇纪基买志静阿诗独复痛消社算' ... '义竟确酒需单治卡幸兰念举仅钟怕共毛句息功官待究跟穿室易游程号居考突皮哪费倒价图具刚脑永歌响商礼细专黄块脚味灵改据般破引食仍存众注笔甚某沉血备习校默务土微娘须试怀料调广蜖苏显赛查密议底列富梦错座参八除跑' ]; end properties dictParent dictChar hashParent hashChar hashVal queue qHead qTail nextCode end methods function obj = LZW () obj.dictParent = zeros (1 , LZW.MAX_SIZE, 'int32' ); obj.dictChar = zeros (1 , LZW.MAX_SIZE, 'uint8' ); obj.hashParent = zeros (1 , LZW.HASH_SIZE, 'int32' ); obj.hashChar = zeros (1 , LZW.HASH_SIZE, 'uint8' ); obj.hashVal = zeros (1 , LZW.HASH_SIZE, 'int32' ); obj.queue = zeros (1 , LZW.MAX_SIZE, 'int32' ); obj.qHead = 0 ; obj.qTail = 0 ; obj.nextCode = 0 ; end function dictInit (obj) obj.hashVal(:) = -1 ; obj.dictParent(:) = -1 ; obj.dictParent(1 ) = -1 ; obj.dictChar(1 ) = 0 ; obj.nextCode = 1 ; obj.qHead = 0 ; obj.qTail = 0 ; for i = 0 :255 obj.dictParent(obj.nextCode + 1 ) = 0 ; obj.dictChar(obj.nextCode + 1 ) = uint8(i ); obj.hashInsert(0 , uint8(i ), obj.nextCode); obj.queue(obj.qTail + 1 ) = obj.nextCode; obj.qTail = mod (obj.qTail + 1 , LZW.MAX_SIZE); obj.nextCode = obj.nextCode + 1 ; end for i = 1 :length (obj.CHINESE_DICT) utf8 = unicode2native(obj.CHINESE_DICT(i ), 'UTF-8' ); parent = 0 ; for j = 1 :length (utf8) next = obj.hashFind(parent, utf8(j )); if next == -1 next = obj.addNode(parent, utf8(j )); end parent = next; end end end function pos = hashFunc (obj, parent, ch) pos = uint32(mod (uint32(parent) * 131 + uint32(ch), LZW.HASH_SIZE)) + 1 ; end function idx = hashFind (obj, parent, ch) pos = obj.hashFunc(parent, ch); while obj.hashVal(pos) ~= -1 if obj.hashParent(pos) == parent && obj.hashChar(pos) == ch idx = obj.hashVal(pos); return ; end pos = mod (pos, LZW.HASH_SIZE) + 1 ; end idx = -1 ; end function hashInsert (obj, parent, ch, idx) pos = obj.hashFunc(parent, ch); while obj.hashVal(pos) ~= -1 pos = mod (pos, LZW.HASH_SIZE) + 1 ; end obj.hashParent(pos) = parent; obj.hashChar(pos) = ch; obj.hashVal(pos) = idx; end function idx = addNode (obj, parent, ch) if obj.nextCode < LZW.MAX_SIZE idx = obj.nextCode; obj.nextCode = obj.nextCode + 1 ; else idx = obj.queue(obj.qHead + 1 ); obj.qHead = mod (obj.qHead + 1 , LZW.MAX_SIZE); oldParent = obj.dictParent(idx + 1 ); oldCh = obj.dictChar(idx + 1 ); pos = obj.hashFunc(oldParent, oldCh); while ~(obj.hashParent(pos) == oldParent && obj.hashChar(pos) == oldCh) pos = mod (pos, LZW.HASH_SIZE) + 1 ; end obj.hashVal(pos) = -1 ; nextPos = mod (pos, LZW.HASH_SIZE) + 1 ; while obj.hashVal(nextPos) ~= -1 tp = obj.hashParent(nextPos); tc = obj.hashChar(nextPos); tv = obj.hashVal(nextPos); obj.hashVal(nextPos) = -1 ; obj.hashInsert(tp, tc, tv); nextPos = mod (nextPos, LZW.HASH_SIZE) + 1 ; end end obj.dictParent(idx + 1 ) = parent; obj.dictChar(idx + 1 ) = ch; obj.hashInsert(parent, ch, idx); obj.queue(obj.qTail + 1 ) = idx; obj.qTail = mod (obj.qTail + 1 , LZW.MAX_SIZE); end function out = packBits (obj, codes) out = zeros (1 , length (codes) * 3 , 'uint8' ); outPos = 1 ; bitBuf = uint32(0 ); bits = 0 ; for i = 1 :length (codes) bitBuf = bitor(bitshift(bitBuf, LZW.MAX_BITS), bitand(uint32(codes(i )), 2 ^LZW.MAX_BITS - 1 )); bits = bits + LZW.MAX_BITS; while bits >= 8 bits = bits - 8 ; out(outPos) = uint8(bitand(bitshift(bitBuf, -bits), 255 )); outPos = outPos + 1 ; end end if bits > 0 out(outPos) = uint8(bitand(bitshift(bitBuf, 8 - bits), 255 )); outPos = outPos + 1 ; end out = out(1 :outPos-1 ); end function codes = unpackBits (obj, data) codes = zeros (1 , length (data) * 8 / LZW.MAX_BITS + 1 , 'int32' ); codeCount = 1 ; bitBuf = uint32(0 ); bits = 0 ; for i = 1 :length (data) bitBuf = bitor(bitshift(bitBuf, 8 ), uint32(data(i ))); bits = bits + 8 ; while bits >= LZW.MAX_BITS bits = bits - LZW.MAX_BITS; codes(codeCount) = int32(bitand(bitshift(bitBuf, -bits), 2 ^LZW.MAX_BITS - 1 )); codeCount = codeCount + 1 ; end end if bits >= LZW.MAX_BITS codes(codeCount) = int32(bitand(bitshift(bitBuf, -(bits - LZW.MAX_BITS)), 2 ^LZW.MAX_BITS - 1 )); codeCount = codeCount + 1 ; end codes = codes(1 :codeCount-1 ); end function out = compress (obj, input) codes = zeros (1 , length (input), 'int32' ); codeCount = 1 ; parent = 0 ; for i = 1 :length (input) next = obj.hashFind(parent, input(i )); if next ~= -1 parent = next; else codes(codeCount) = parent; codeCount = codeCount + 1 ; obj.addNode(parent, input(i )); parent = obj.hashFind(0 , input(i )); end end if parent ~= 0 codes(codeCount) = parent; codeCount = codeCount + 1 ; end out = obj.packBits(codes(1 :codeCount-1 )); end function out = decompress (obj, input) codes = obj.unpackBits(input); out = zeros (1 , length (input) * 4 , 'uint8' ); outPos = 1 ; prevCode = 0 ; firstCh = uint8(0 ); stack = zeros (1 , LZW.MAX_SIZE, 'uint8' ); for i = 1 :length (codes) top = 1 ; cur = codes(i ); if cur == obj.nextCode && prevCode ~= 0 cur = prevCode; stack(top) = firstCh; top = top + 1 ; elseif cur > obj.nextCode error('无效的压缩数据' ); end while cur ~= 0 stack(top) = obj.dictChar(cur + 1 ); top = top + 1 ; cur = obj.dictParent(cur + 1 ); end firstCh = stack(top-1 ); for j = top-1 :-1 :1 out(outPos) = stack(j ); outPos = outPos + 1 ; end if prevCode ~= 0 && obj.nextCode < LZW.MAX_SIZE obj.addNode(prevCode, firstCh); end prevCode = codes(i ); end out = out(1 :outPos-1 ); end end end function main () fprintf('------------------------------------\n' ); fprintf(' 示例:lzw.m 您的文件路径,未提供参数,使用默认 Twilight.txt\n' ); fprintf('------------------------------------\n' ); if nargin < 1 inputPath = 'Twilight.txt' ; else inputPath = varargin{1 }; end try fid = fopen(inputPath, 'rb' ); if fid == -1 error('无法打开文件' ); end input = fread(fid, '*uint8' ); fclose(fid); catch e fprintf('读取文件失败: %s\n' , e.message); return ; end [~, name, ~] = fileparts(inputPath); compPath = [name '.lzw' ]; decompPath = [name '.dec' ]; compressor = LZW(); compressor.dictInit(); tic; compressed = compressor.compress(input); compressTime = toc; try fid = fopen(compPath, 'wb' ); if fid == -1 error('无法创建压缩文件' ); end fwrite(fid, compressed, 'uint8' ); fclose(fid); catch e fprintf('写入压缩文件失败: %s\n' , e.message); return ; end fprintf('压缩完成: %d -> %d bytes, 用时 %.3fs, 文件保存路径 %s\n' , ... length (input), length (compressed), compressTime, compPath); decompressor = LZW(); decompressor.dictInit(); tic; decompressed = decompressor.decompress(compressed); decompressTime = toc; try fid = fopen(decompPath, 'wb' ); if fid == -1 error('无法创建解压文件' ); end fwrite(fid, decompressed, 'uint8' ); fclose(fid); catch e fprintf('写入解压文件失败: %s\n' , e.message); return ; end fprintf('解压完成: %d bytes, 用时 %.3fs\n' , ... length (decompressed), decompressTime); if length (input) ~= length (decompressed) fprintf('长度不匹配: 原始=%d, 解压=%d\n' , length (input), length (decompressed)); end diffCount = 0 ; for i = 1 :min (length (input), length (decompressed)) if input(i ) ~= decompressed(i ) diffCount = diffCount + 1 ; if diffCount <= 10 fprintf('位置 %d: 原始=%d, 解压=%d\n' , i , input(i ), decompressed(i )); end end end if diffCount > 0 fprintf('共发现 %d 处差异\n' , diffCount); else fprintf('校验通过\n' ); end end
1.5.2 性能测试 性能测试包括压缩率测试和压缩速度测试,针对 Python、C、Java、JavaScript 和 Go 五个版本进行评估。测试数据集涵盖三类文本:纯英文小说《The Count of Monte Cristo.txt》、中文小说《三体全集.txt》以及中英混合小说《Twilight.txt》。结果如下:
语言
《The Count of Monte Cristo.txt》压缩率
《三体全集.txt》压缩率
《Twilight.txt》压缩率
C
997113 / 2645466 ≈ 37.691%
1058935 / 1857417 ≈ 57.011%
625005 / 1335182 ≈ 46.810%
Go
997113 / 2645466 ≈ 37.691%
1060219 / 1857417 ≈ 57.080%
623694 / 1335182 ≈ 46.712%
Python
997113 / 2645466 ≈ 37.691%
1059894 / 1857417 ≈ 57.062%
623868 / 1335182 ≈ 46.726%
Java
997113 / 2645466 ≈ 37.691%
1060219 / 1857417 ≈ 57.080%
623694 / 1335182 ≈ 46.712%
JavaScript
997113 / 2645466 ≈ 37.691%
1060219 / 1857417 ≈ 57.080%
623694 / 1335182 ≈ 46.712%
表 1.13 压缩率对比 图 1.5 各语言压缩率对比柱状图
语言
《The Count of Monte Cristo.txt》压缩时间(s)
《三体全集.txt》压缩时间(s)
《Twilight.txt》压缩时间(s)
C
0.075
0.039
0.031
Python
0.093
0.062
0.076
Java
0.156
0.140
0.082
JavaScript
0.114
0.096
0.068
Go
0.052
0.050
0.026
表 1.14 压缩时间对比 图 1.6 各语言压缩时间对比柱状图 分析结果可知:各语言在三个文本上的压缩率差异很小,几乎一致,对于英文文本压缩率完全相同。至于中英文文本上略有细微差别,Python 在纯中文文本上略低一些。在压缩时间上,C 和 Go 的压缩速度最快,Go 略优于 C,Java 压缩速度最慢,Python 和 JavaScript 表现中等,Python 稍快于 JS。
2. 应用 LZW 算法利用了数据内部的重复模式,无需预先知道数据的概率分布,因此算法结构相对简单。像英文文本和数字图像这样的数据,本身就有很强的重复性(比如相邻字符或像素相似),这使得 LZW 压缩效果特别好。由于这种优势,LZW 被广泛应用于图像和文档格式中,比如 GIF 和 TIFF 图像格式,以及早期的 PDF 文件中,用来压缩图像或文字内容。特别是在 GIF 格式中,LZW 现在仍是核心压缩算法。
2.1 在 GIF 图像中的应用 2.1.1 GIF 简介 GIF(Graphics Interchange Format,图形交换格式)是一种无损压缩的点阵图像格式,由 CompuServe 于 1987 年推出。由美国在线服务公司 CompuServe 于 1987 年开发。它因体积小、易传输,很快成为早期互联网中最流行的图片格式之一。
GIF 的特点包括:
支持动画:可以播放连续画面,实现简单动画效果;
支持透明背景:方便叠加在其他图像上;
采用 LZW 压缩算法:保证压缩效率和速度,同时不损失图像质量;
颜色限制为 256 色:每张图最多只能用 256 种颜色,适合色彩简单且具有大面积单色区域的图像,比如图标、线条画、按钮、表情包等。
正因为颜色数量有限,GIF 并不适合用来存储照片或色彩渐变丰富的图像,这些场景下不仅压缩效果差,文件反而更大。尽管现在有了更高效的格式如 WebP 和 AVIF,GIF 仍因其兼容性和无需插件的优势,在表情包和轻量级动画中保持着不可替代的地位。
2.1.2 GIF 文件格式 一个 GIF 文件由多个部分组成,每一部分都有特定的功能,共同组成一幅静态图或动画。以下是 GIF 文件的基本结构:
文件头(GIF Signature) :告诉系统这是一个 GIF 文件,并标明它使用的版本(比如 GIF87a 或 GIF89a)。屏幕描述符 :定义整个画布的尺寸(宽高)、颜色深度、背景色等属性。全局颜色表(可选) :如果有这部分,它会列出整个 GIF 使用的颜色列表。图像中的颜色都会从这里选,最多 256 种。图像数据块 :这是最重要的部分,存放实际的图像内容。每个数据块就像动画中的一帧,里面的图像数据已经通过 LZW 算法压缩过。扩展数据块(可选) :包含一些额外信息,比如动画控制、注释、透明度设置等。它不是必须的,但对实现动画或特效很有用。文件尾(GIF Trailer) :表示文件结束。
我们以一个具体的 GIF 文件为例,使用十六进制编辑器(如 010 Editor)进行逐段分析,来直观地说明 GIF 文件的各个组成部分。
图 2.1 GIF 文件头部分 图 2.2 GIF 文件数据部分
文件头(前 6 个字节):47 49 46 38 39 61
逻辑描述块,包括屏幕描述符和全局颜色表(7+N 字节):
扩展块(以 0x21 开头,多个子块)
应用扩展(Netscape 动画循环次数,关键子块):21 FF 0B 4E 45 54 53 43 41 50 45 32 2E 30 03 01 00 00 00
扩展标识符:21 FF → 通用扩展块标识(Application Extension)。
块大小:0B → 后续数据长度为 11 字节。
应用标识符:4E 45 54 53 43 41 50 45 32 2E 30 → “NETSCAPE2.0”(Netscape 浏览器自定义扩展)。
循环次数:03 01 00 00,第 3、4 字节表示 gif 的循环播放次数,如果是 0x0000 表示无限循环。
图形控制扩展(控制单帧显示效果):21 F9 04 00 32 00 00 00
扩展标识符:21F9 → 图形控制扩展(Graphic Control Extension)。
块大小:04 → 后续 4 字节为有效数据。
标志位:00 → 该帧未启用透明色(第 6–5 位为 00),处置方式为“无操作”(第 2–0 位为 000),即当前帧显示后不清除,下一帧直接覆盖显示在其上。
延迟时间:32 00 → 小端序 0x0032,每帧显示 500 毫秒。
透明颜色索引:00。
图像数据块(以 0x2C 开头,单帧图像)
图像标识符(1 字节):2C。
图像位置(4 字节,小端序):00 00 00 00 → X=0 像素,Y=0 像素(图像左上角位于屏幕原点)。
图像大小(4 字节,小端序):32 00 32 00 → 宽度=200 像素,高度=174 像素(与屏幕尺寸一致,无裁剪或偏移)。
LZW 数据块:08 FF 00 11 08 1C 48 B0 60 82 83 02 A1... FF .... FF ... 00
文件结束符(最后 1 字节):3B → GIF 文件结束标志。
整体结构图如图 2.3 所示:
图 2.3 GIF 文件结构图 2.1.3 LZW 压缩 那么 LZW 对什么数据进行压缩呢?GIF 图像通过全局/局部调色板表示颜色,每个像素不直接存储 RGB 值,而是存储一个索引,指向调色板中的颜色。LZW 压缩的对象正是这些颜色索引值的序列 。在保存为 GIF 格式时,图像像素首先被转换为调色板索引,然后这组索引作为输入数据传入 LZW 编码器进行压缩。压缩后的结果就是写入 GIF 文件中的图像数据部分。
3. 联合加密方案 在当今高度重视隐私和网络安全的社会背景下,压缩算法作为一种可逆过程,本身并不具备安全性。一旦压缩数据被获取,就可以被还原为原始内容。因此,如何保护压缩数据的安全性成为一个研究课题。
最直接的方法是“先压缩,后加密 ”,将压缩和加密作为两个独立步骤处理。但这种做法效率较低,尤其在对实时性要求较高的场景中,表现不佳。
为提高处理效率,越来越多的研究聚焦于压缩与加密的融合,即在压缩过程中直接引入加密机制,实现同步压缩与加密。许多学者在这一方向上提出了不同的改进方案,以下将介绍几种典型的 LZW 加密压缩联合方法。
3.1 置乱字典 这种方法通过对 LZW 字典按特定规则重新排序,实现加密效果。由于字典顺序被打乱,常规的解码器难以预测索引,只有掌握置乱规则的人才能正确还原原始数据。以下以 Zhou[9] 等人于 2008 年提出的方法为例:该方法将 LZW 字典构建为二维数组结构,并在压缩过程中不断对字典内容进行置乱,从而实现压缩与加密同步进行。
3.1.1 算法流程 使用固定编码长度为 b 位的字典,b 是一个偶数,这里选择 b=12,即字典大小为 4096。首先创建初始字典,将初始字符通过带密钥的哈希函数随机插入到字典中。在加密压缩过程中,首先对明文执行标准的 LZW 压缩。唯一的区别在于:当需要将新字符串 P+C 添加到字典时,不再顺序插入,而是通过带密钥的哈希函数随机选择一个空位置插入。每次添加之后,对整个字典进行置乱处理。具体做法如下:
把字典组织成一个 $ 2^{b/2} \times 2^{b/2} $ 的二维数组。
列循环移位:奇数列以随机步长 $ c_1 $($ 0 \le c_1 \le 2^{b/2}-1 $)作循环右移,偶数列以随机步长 $ c_2 $($ 0 \le c_2 \le 2^{b/2}-1 $)作循环右移。
行循环移位:奇数行整体循环移位 $ r_1 $,偶数行整体循环移位 $ r_2 $。
以 $ b = 4, c_1 = 2, c_2 = 3, r_1 = 1, r_2 = 2 $ 为例,置乱过程如图 3.1 所示:
图 3.1 字典置乱举例 在所有字符完成压缩加密后,解密与解压缩过程依赖相同的密钥来重构与编码时一致的字典顺序。由于插入位置是通过带密钥的哈希函数确定的,未持有密钥的攻击者无法准确还原字典结构,因此无法解密数据。
除此之外,整个算法由包括两部分,除了改进的 LZW 算法外,还有一个密钥调度程序(Key Scheduling Algorithm),其功能就是产生出指定位数密钥流,密钥流一部分来实施安全压缩,另一部分作为掩码用于与结果数据进行异或。算法原理图如图 3.2 所示。
图 3.2 算法原理图 接下来我们从两个方面对方案进行分析,首先是方案安全性:
哈希函数密钥:采用 128 位密钥,密钥空间为 $ 2^{128} $,满足安全级别要求。
从编码入手暴力破解:若尝试枚举所有可能的字典插入顺序,等价于对 $ 2^{b} $ 个条目的全排列进行穷举,即需要 $ 2^b!=4096! $ 次尝试,也具备强安全性。
接下来是效率方面,该方案由于字典条目是随机插入和置换的,索引无法递增,只能固定用 b 位编码,相比于原始 LZW 的可变长度编码,效率损失明显。
3.1.2 代码实现 此处仅展示 Python 的参考实现。哈希函数采用 SHA256,密钥流由 128 位 RC4 流密码生成。通过维护一个空位索引列表,并结合带密钥的哈希函数进行随机选择,实现了在数组中高效且精确地定位可用插入位置。采用字典重置方式进行字典更新。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 import hashlibimport osimport timeimport uuidfrom typing import List , Optional , Union class RC4KeyScheduler : def __init__ (self, key: Union [bytes , str ] ): """ 初始化 RC4 密钥调度器(KSA) :param key: RC4 密钥,必须为 1~256 字节,支持 str 或 bytes """ if isinstance (key, str ): key = key.encode() if not (1 <= len (key) <= 256 ): raise ValueError("密钥长度必须在 1 到 256 字节之间" ) self ._S = self ._ksa(key) self ._i = 0 self ._j = 0 @staticmethod def _ksa (key: bytes ) -> List [int ]: """ 执行 Key Scheduling Algorithm(KSA)初始化 S 数组 :param key: 输入密钥 :return: 初始化后的 S 向量 """ key_len = len (key) S = list (range (256 )) j = 0 for i in range (256 ): j = (j + S[i] + key[i % key_len]) & 0xFF S[i], S[j] = S[j], S[i] return S def generate_key_stream (self, length: int ) -> bytes : """ 使用伪随机生成算法(PRGA)生成密钥流 :param length: 所需生成的字节数 :return: 密钥流字节序列(bytes) """ if length <= 0 : raise ValueError("密钥流长度必须大于 0" ) S = self ._S[:] i, j = self ._i, self ._j stream = bytearray (length) for idx in range (length): i = (i + 1 ) & 0xFF j = (j + S[i]) & 0xFF S[i], S[j] = S[j], S[i] K = S[(S[i] + S[j]) & 0xFF ] stream[idx] = K self ._i = i self ._j = j return bytes (stream) class LZW : def __init__ (self, key: str = '65691f00-5474-4e16-8256-2e2dc711e67d' , initial_chars: Optional [List [bytes ]] = None ): """ 初始化 LZW 压缩器 :param key: 用于加密置乱的密钥 :param initial_chars: 初始字符集,默认为256个ASCII字符 """ self .key = key self .b = 10 self .dict_size = 1 << self .b self .matrix_size = 1 << (self .b // 2 ) self .initial_chars = initial_chars or [bytes ([i]) for i in range (256 )] self .key_stream = RC4KeyScheduler(key=key).generate_key_stream(128 ) self .pos_shift = { 'c1' : self .key_stream[0 ], 'c2' : self .key_stream[1 ], 'r1' : self .key_stream[2 ], 'r2' : self .key_stream[3 ] } def _init_dictionary (self ) -> List [Optional [bytes ]]: """ 使用带密钥哈希初始化字典,避免重复条目 """ dictionary = [None ] * self .dict_size for c in self .initial_chars: pos = self .keyed_hash(c, self .key, self .dict_size) while dictionary[pos] is not None : pos = (pos + 1 ) % self .dict_size dictionary[pos] = c return dictionary def _scramble (self, dictionary: List [Optional [bytes ]] ) -> List [Optional [bytes ]]: """ 使用循环移位操作,对字典执行矩阵置乱处理,提高安全性 """ size = self .matrix_size matrix = [dictionary[i * size:(i + 1 ) * size] for i in range (size)] for col in range (size): shift = self .pos_shift['c1' ] if col % 2 else self .pos_shift['c2' ] if shift: column = [matrix[row][col] for row in range (size)] shifted = column[-shift:] + column[:-shift] for row in range (size): matrix[row][col] = shifted[row] for row in range (size): shift = self .pos_shift['r1' ] if row % 2 else self .pos_shift['r2' ] if shift: matrix[row] = matrix[row][-shift:] + matrix[row][:-shift] return [item for row in matrix for item in row] def _xor_encrypt (self, data: bytes ) -> bytes : """ 使用密钥流对数据进行按位异或加密/解密(对称) """ ks = self .key_stream[4 :] return bytes ([b ^ ks[i % len (ks)] for i, b in enumerate (data)]) def _pack_bits (self, codes: List [int ] ) -> bytes : """ 将整数编码列表压缩成位流(按 self.b 位打包) """ buf, bits, out = 0 , 0 , bytearray () for code in codes: buf = (buf << self .b) | code bits += self .b while bits >= 8 : bits -= 8 out.append((buf >> bits) & 0xFF ) if bits: out.append((buf << (8 - bits)) & 0xFF ) return bytes (out) def _unpack_bits (self, data: bytes ) -> List [int ]: """ 将位流还原为整数编码列表 """ buf, bits, codes = 0 , 0 , [] for byte in data: buf = (buf << 8 ) | byte bits += 8 while bits >= self .b: bits -= self .b codes.append((buf >> bits) & ((1 << self .b) - 1 )) return codes def compress (self, data: bytes ) -> bytes : """ 对输入字节流执行加密压缩,返回加密后的压缩流 """ dictionary = self ._init_dictionary() output = [] current = b'' for byte in data: next_seq = current + bytes ([byte]) if next_seq in dictionary: current = next_seq continue output.append(dictionary.index(current)) dictionary = self ._insert_sequence(dictionary, next_seq) current = bytes ([byte]) if current: output.append(dictionary.index(current)) packed = self ._pack_bits(output) return self ._xor_encrypt(packed) def decompress (self, data: bytes ) -> bytes : """ 对加密压缩流执行解压缩还原原始字节流 """ dictionary = self ._init_dictionary() codes = self ._unpack_bits(self ._xor_encrypt(data)) output = bytearray () prev = dictionary[codes[0 ]] if prev is None : raise ValueError(f"解码错误,找不到编码: {codes[0 ]} " ) output += prev for code in codes[1 :]: dictionary = self ._scramble(dictionary) entry = dictionary[code] if dictionary[code] else prev + bytes ([prev[0 ]]) output += entry new_seq = prev + bytes ([entry[0 ]]) dictionary = self ._insert_sequence(dictionary, new_seq) prev = entry return bytes (output) def _insert_sequence (self, dictionary: List [Optional [bytes ]], seq: bytes ) -> List [Optional [bytes ]]: """ 向字典中插入新序列,并在必要时执行置乱和重建 """ empty_indices = [i for i, v in enumerate (dictionary) if v is None ] if not empty_indices: dictionary = self ._init_dictionary() empty_indices = [i for i, v in enumerate (dictionary) if v is None ] pos = self .keyed_hash(seq, self .key, len (empty_indices)) dictionary[empty_indices[pos]] = seq return self ._scramble(dictionary) def compress_file (self, file_path: str ) -> str : """ 压缩文件,并生成 .lzw 文件 """ with open (file_path, "rb" ) as f: data = f.read() compressed = self .compress(data) comp_path = os.path.splitext(file_path)[0 ] + ".lzw" with open (comp_path, "wb" ) as f: f.write(compressed) print (f"压缩成功: {comp_path} , 原始: {len (data)} → 压缩后: {len (compressed)} 字节" ) return comp_path def decompress_file (self, file_path: str ) -> str : """ 解压文件,生成 .dec 文件 """ with open (file_path, "rb" ) as f: compressed = f.read() data = self .decompress(compressed) out_path = os.path.splitext(file_path)[0 ] + ".dec" with open (out_path, "wb" ) as f: f.write(data) print (f"解压成功: {out_path} , 解压大小: {len (data)} 字节" ) return out_path @staticmethod def keyed_hash (data: bytes , key: str , mod: int ) -> int : """ 使用 SHA256 对 key+data 生成哈希索引 """ if isinstance (key, str ): key = key.encode() digest = hashlib.sha256(key + data).digest() return int .from_bytes(digest, 'big' ) % mod if __name__ == "__main__" : key = str (uuid.uuid4()) lzw = LZW(key=key) file_path = r"D:\TheCountof.txt" start_time = time.time() com_file_path = lzw.compress_file(file_path) end_time = time.time() print (f"压缩时间: {end_time - start_time:.3 f} 秒" ) start_time = time.time() dec_file_path = lzw.decompress_file(com_file_path) end_time = time.time() print (f"解压缩时间: {end_time - start_time:.3 f} 秒" ) with open (file_path, "rb" ) as f: t1 = f.read() with open (dec_file_path, "rb" ) as f: t2 = f.read() if t1 == t2: print ("校验通过" )
3.1.3 攻击原理 2011 年,Li[10] 等人分析了该方案的算法安全性,指出其存在缺陷,并给出了可行的选择明文攻击和选择密文攻击方法。下面我们将对这一攻击过程进行复现与验证。
Zhou 等人的方法建立在两个安全前提之上:
攻击者必须逐个穷举密钥调度程序生成的密钥流中的每个元素;
由于密钥流具有前向依赖性,猜测第 $ i $ 个密钥元素 $ K_i $ 之前,必须先成功猜出前面所有的密钥 $ K_1, K_2, …, K_{i-1} $。
但当我们只关注字典中的 “单符号初始条目”(初始字典里预先存好的单个字符,如字母 a、b、c 等),Zhou 的两个假设就不成立了。原因在于单符号条目的特殊性:
这些条目在整个加密压缩过程开始前就已经被插入字典,不需要等加密过程中遇到新字符串才添加;
它们在每一步编码结束后会被随机置换位置,但更新是全局同步的,无论明文是什么,所有单符号条目的更新规则只受密钥参数(如 $ c_1,\ c_2,\ r_1,\ r_2 $)控制,和具体的明文无关。
因此我们可以发现:如果两个任意明文中第 $ i $ 个被编号的字符串($ S_i,\ S_i^{\ \prime} $)在字典中是单符号,那么只有当这两个符号完全相同时,他们的密文索引 $ B_i $ 和 $ B_i^{\ \prime} $ 才会相同。
证明:由于初始条目的置换方式仅由密钥决定,且该密钥在整个加密压缩过程中保持不变,因此所有初始单符号的排列顺序在整个过程中都是固定的。设 $ S_i $ 和 $ S_i^{\ \prime} $ 是两个不同明文的第$ i $个被编码字符串,如果它们都是单个符号 $ a $,那么在经历 $ i $ 次编码后,两个对应的字典 $ D_i $ 和 $ D_i^{\ \prime} $ 中,符号 $ a $ 的索引位置是相同的,即 $ D_i(a) = D_i^{\ \prime}(a) $。密文索引的计算方式为 $ D_i(a) \oplus K_i $。由于异或操作是可逆的,且密钥流 $ K_i $ 相同,那么只要 $ S_i= S_i^{\ \prime} $,就有 $ B_i= B_i^{\ \prime} $。反过来说,如果 $ B_i= B_i^{\ \prime} $,也可以推出 $ S_i= S_i^{\ \prime} $。
3.1.4 攻击方案 利用上述定理,攻击者可以发起针对单符号条目的选择明文攻击 ,步骤如下:
构造明文 :攻击者主动选择大量包含单符号的明文,比如设计 $ n $ 个明文,$ n $ 是字母表的大小,比如英语有 98 个可打印 ASCII 字符,每个明文的结构是单符号的不同排列组合,例如:
明文 1:先出现字母 1(如 A),然后字母 2(B),依此类推,覆盖所有单符号的组合;
明文 2:类似结构,但起始字母不同(如从 B 开始);
……
明文 n:覆盖最后一个字母的组合。
**构建查找表(look-up table LUT):**观察每个单符号对应的密文索引 $ B_i $。由于前面保证 “相同单符号对应相同 $ B_i $,不同单符号对应不同 $ B_i $,攻击者可以记录每个单符号 $ a $ 和其密文索引 $ B_i $ 的对应关系,形成一个查找表 $ LUT_i = {(a,\ D_i (a) \oplus K_i)}_{1 \le i \le L} $,其中 $ i $ 是编码步骤,$ L $ 是需要处理的最大密文数量。
破解密文 :当攻击者截获到一个密文索引 $ B_i $ 时,只需检查 $ B_i $ 是否存在于 $ LUT_i $ 中。如果存在,就能直接对应到对应的单符号明文 $ S_i $。
选择密文攻击 的思路和之前的“选择明文攻击”类似,但攻击者的操作方向相反,虽然步骤比“选择明文攻击”多(效率低一点),但依然能破解单符号密文。
攻击者的目标仍是识别哪些密文索引对应单符号条目。但因为字典里有些位置是空的(无效条目),攻击者没法直接知道哪些密文对应有效的单符号,所以得逐步试探:
先遍历 $ 2^b $ 个第一位密文(覆盖所有可能的 b 位索引,比如 b=3 时,有 8 种可能的密文:000、001…111),把这些密文发给解密器,观察哪些密文能解出有效的单符号,记录下来形成第 1 个查找表 LUT1(类似“001→a,010→b…”)。
结合上一个密文,再生成所有可能的 2 位密文,重复操作,形成第 2 个查找表 LUT2(记录第 2 步的密文和单符号对应关系)……
直到生成 L 个查找表(覆盖 L 个步骤),就能知道每个步骤中哪些密文对应哪个单符号。
攻击效果:
虽然这种攻击只能直接破解单字符对应的密文(如字母、空格等),但由于单字符在明文中出现频率很高,尤其常见于文本开头,攻击者可以通过查找表“对号入座”,轻松还原这些字符,造成信息泄露。字典越小,单符号出现越频繁,泄露风险越大。尽管攻击对多字符字符串效果较弱,但只要能还原开头部分,就可能暴露关键信息,且结合语言模式还可能进一步推测后续内容。
攻击局限性 :
攻击效果受限于字典大小和明文特性:理论上,如果字典已存满所有可能的两字符组合(如aa、ab等),LZW 会优先使用这些更长的词条进行编码,导致单字符的密文索引 $ B_i $ 不再出现,使查找表无法继续扩展。但在实际应用中,这种情况极少发生。一方面,自然语言中的两字符组合数量有限,很多组合根本不会出现;另一方面,字典容量通常不足以容纳所有两字符组合。因此,字典“完全覆盖两字符字符串”的情况要么不可能,要么极为罕见。
对图像无效:因为图像中的多符号字符串(比如连续像素组合)长度不固定,且泄露的单个像素无法还原图像结构(比如一个像素的颜色无法推断整幅图的内容),因此该算法可能仍适用于图像加密。
攻击脚本(Python):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 import jsonimport stringfrom pathlib import Pathfrom typing import Any , Dict , List , Optional from concurrent.futures import ProcessPoolExecutorfrom tqdm import tqdmfrom Zhou_lzw import LZWclass ZhouLZWCPA : """ LZW CPA 攻击解密器类:通过构建查找表实现密文解码 """ BITS_PER_CODE = 10 PAD_CHAR_RANGE = range (32 , 127 ) CHARACTER_TABLE = string.ascii_letters + string.digits + " ,.{}\"\'-!" def __init__ (self, lut_path: Path, lzw_instance: Any , regenerate_lut: bool = False , pad_range: range = range (0 , 200 ): """ 初始化 ZhouLZWCPA 解密器 :param lut_path: 查找表路径(JSON) :param lzw_instance: 支持 compress 方法的 LZW 实例 :param regenerate_lut: 是否强制重建查找表 :param pad_range: 查找表构建时使用的填充步长范围 """ self .lut_path = lut_path self .lzw = lzw_instance self .regenerate_lut = regenerate_lut self .pad_range = pad_range self .lut: Dict [str , Dict [str , str ]] = {} @staticmethod def _unpack_bits (data: bytes ) -> List [int ]: """ 将字节流按位解码为整数索引列表(基于固定比特长度) """ result, bitbuf, bits = [], 0 , 0 for byte in data: bitbuf = (bitbuf << 8 ) | byte bits += 8 while bits >= ZhouLZWCPA.BITS_PER_CODE: bits -= ZhouLZWCPA.BITS_PER_CODE result.append((bitbuf >> bits) & ((1 << ZhouLZWCPA.BITS_PER_CODE) - 1 )) bitbuf &= (1 << bits) - 1 return result def _generate_padded_input (self, char: str , pad_len: int ) -> str : """ 生成指定字符的填充明文字符串 :param char: 明文字符 :param pad_len: 填充长度 :return: 带填充的明文 """ padding, count = [], 0 for i in ZhouLZWCPA.PAD_CHAR_RANGE: if chr (i) in char: continue use = min (2 , pad_len - count) padding.append(chr (i) * use) count += use if count >= pad_len: break return '' .join(padding) + char def _generate_plaintexts (self, pad: int ) -> List [str ]: """ 构造当前 pad 值对应的所有测试明文列表 """ return [self ._generate_padded_input(ch, pad) for ch in ZhouLZWCPA.CHARACTER_TABLE] def _build_single_lut (self, pad: int ) -> Dict [int , str ]: """ 构建特定填充步长 pad 下的查找表 :param pad: 当前步长 :return: 查找表 {index: character} """ lut = {} for plaintext in tqdm(self ._generate_plaintexts(pad), desc=f"构建查找表步长: {pad} " ): try : encoded = self .lzw.compress(plaintext.encode()) index_list = self ._unpack_bits(encoded) lut[index_list[pad]] = plaintext[pad] except Exception: continue return lut def _load_or_generate_lut (self ) -> bool : """ 加载或生成所有步长的查找表 :return: 是否成功 """ if self .regenerate_lut or not self .lut_path.exists(): try : print ("开始构建查找表..." ) with ProcessPoolExecutor() as executor: results = list (executor.map (self ._build_single_lut, self .pad_range)) self .lut = {str (p): {str (k): v for k, v in d.items()} for p, d in zip (self .pad_range, results)} with open (self .lut_path, 'w' ) as f: json.dump(self .lut, f, ensure_ascii=False , indent=2 ) print (f"查找表保存成功: {self.lut_path} " ) return True except Exception as e: print (f"查找表构建失败: {e} " ) return False else : try : with open (self .lut_path, 'r' ) as f: self .lut = json.load(f) print (f"成功加载查找表: {self.lut_path} " ) return True except Exception as e: print (f"查找表加载失败: {e} " ) return False def decrypt (self, ciphertext: bytes ) -> Optional [str ]: """ 使用查找表对密文进行解码 :param ciphertext: 密文字节流(经过 LZW 压缩) :return: 解密后的明文字符串或 None """ if not self ._load_or_generate_lut(): return None try : print ("\n开始解密..." ) decrypted = [] indices = self ._unpack_bits(ciphertext) for step, idx in enumerate (indices): char = self .lut.get(str (step), {}).get(str (idx), '*' ) decrypted.append(char) print (f"步骤 {step:02d} : 索引 {idx:04d} -> 明文 '{char} '" ) result = '' .join(decrypted) print ("\n最终解密结果:" , result) return result except Exception as e: print (f"解密失败: {e} " ) return None if __name__ == "__main__" : lut_path = Path("lut.json" ) lzw = LZW() decryptor = ZhouLZWCPA( lut_path=lut_path, lzw_instance=lzw, regenerate_lut=True , pad_range=range (0 , 200 ) ) ciphertext = b'\x15\x98\xdd\xd2KR\xac\xa9U\xac\xb5\xf15j\x17\xebU\xe9\x13\x89\xee\xa0\xfe \x00d:\xa3\x96\xea&\xef\x1cR\x81\xb5\x95\x98\xa0]\xee\x10\x1b\xc23\xf0\xb4\xe3nB;N\x8f6\xe7w\xb2Q\xc5%\xe3)|\xad\x1b\xa2\x08\xe6\xc3\xf8\t<\xefi\\\xcfb\x110r\xf3\x14\x02\x8e\x15"\x13\xc0\xb0\xeb_r\x1c' decrypted = decryptor.decrypt(ciphertext)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 import jsonimport stringfrom pathlib import Pathfrom typing import List , Dict , Optional from tqdm import tqdmfrom Zhou_lzw import LZWclass ZhouLZWCCA : """ LZW CCA 攻击解密器类:通过构建查找表实现密文解码 """ BITS_PER_CODE = 10 PAD_CHAR_RANGE = range (32 , 127 ) CHARACTER_TABLE = string.ascii_letters + string.digits + " ,.{}\"\'-!" def __init__ (self, lut_path: Path, lzw_instance, regenerate_lut: bool = False , pad_range: range = range (0 , 10 ): self .lut_path = lut_path self .lzw = lzw_instance self .regenerate_lut = regenerate_lut self .pad_range = pad_range self .lut: Dict [str , Dict [str , str ]] = {} @staticmethod def _pack_bits (codes: List [int ] ) -> bytes : """将整数编码列表压缩为字节流""" bitbuf = bits = 0 out = bytearray () for code in codes: bitbuf = (bitbuf << ZhouLZWCCA.BITS_PER_CODE) | code bits += ZhouLZWCCA.BITS_PER_CODE while bits >= 8 : bits -= 8 out.append((bitbuf >> bits) & 0xFF ) bitbuf &= (1 << bits) - 1 if bits > 0 : out.append((bitbuf << (8 - bits)) & 0xFF ) return bytes (out) @staticmethod def _unpack_bits (data: bytes ) -> List [int ]: """将字节流解码为整数编码列表""" codes, bitbuf, bits = [], 0 , 0 for byte in data: bitbuf = (bitbuf << 8 ) | byte bits += 8 while bits >= ZhouLZWCCA.BITS_PER_CODE: bits -= ZhouLZWCCA.BITS_PER_CODE codes.append((bitbuf >> bits) & ((1 << ZhouLZWCCA.BITS_PER_CODE) - 1 )) bitbuf &= (1 << bits) - 1 return codes def _generate_ciphertext (self, target_code: List [int ], pad_step: int , prev_lut: Optional [Dict ] = None ) -> bytes : """ 生成带预填充的模拟密文 :param target_code: 当前明文字节对应的编码 :param pad_step: 当前步骤/填充步数 :param prev_lut: 用于构建填充内容的查找表 :return: 模拟密文 """ prefix_codes = [] if prev_lut and pad_step: prefix_codes = [int (next (iter (entry))) for entry in prev_lut.values() if entry] return self ._pack_bits(prefix_codes + target_code) def _construct_test_ciphertexts (self, pad_step: int , prev_lut: Optional [Dict ] ) -> List [bytes ]: """ 为当前步骤构造所有候选密文(每个可能字符一次) """ return [self ._generate_ciphertext([i], pad_step, prev_lut) for i in range (4096 )] def _build_lookup_table (self, step: int , prev_lut: Optional [Dict ] ) -> Dict [int , str ]: """ 构造当前 step 的查找表:密文索引 → 明文字符 """ lookup = {} test_streams = self ._construct_test_ciphertexts(step, prev_lut) for ct in test_streams: try : plaintext = self .lzw.decompress(ct).decode('utf8' ) index_list = self ._unpack_bits(ct) if len (plaintext) == step + 1 : ch = plaintext[step] if ch in self .CHARACTER_TABLE: lookup[index_list[step]] = ch except Exception: continue return lookup def _load_or_generate_lut (self ) -> bool : """ 载入现有查找表或按需构建新查找表 """ if self .regenerate_lut or not self .lut_path.exists(): try : print ("正在构建查找表..." ) for step in tqdm(self .pad_range, desc=f"构建步骤查找表" ): step_lut = self ._build_lookup_table(step, self .lut) self .lut[str (step)] = {str (k): v for k, v in step_lut.items()} with open (self .lut_path, 'w' ) as f: json.dump(self .lut, f, ensure_ascii=False , indent=2 ) print (f"查找表保存成功: {self.lut_path} " ) return True except Exception as e: print (f"查找表构建失败: {e} " ) return False else : try : with open (self .lut_path, 'r' ) as f: self .lut = json.load(f) print (f"查找表加载成功: {self.lut_path} " ) return True except Exception as e: print (f"查找表加载失败: {e} " ) return False def decrypt (self, ciphertext: bytes ) -> Optional [str ]: """ 使用查找表解密密文 :param ciphertext: 压缩后的密文字节流 :return: 解密出的明文或 None """ if not self ._load_or_generate_lut(): return None try : print ("\n开始解密..." ) result = [] index_list = self ._unpack_bits(ciphertext) for step, code in enumerate (index_list): ch = self .lut.get(str (step), {}).get(str (code), '*' ) result.append(ch) print (f"步骤 {step:02d} : 索引 {code:04d} → 字符 '{ch} '" ) final_text = '' .join(result) print ("\n最终解密结果:" , final_text) return final_text except Exception as e: print (f"解密失败: {e} " ) return None if __name__ == "__main__" : lut_path = Path("lut.json" ) lzw = LZW() decryptor = ZhouLZWCCA( lut_path=lut_path, lzw_instance=lzw, regenerate_lut=True , pad_range=range (0 , 10 ) ) ciphertext = b'\x15\x98\xdd\xd2KR\xac\xa9U\xac\xb5\xf15j\x17\xebU\xe9\x13\x89\xee\xa0\xfe \x00d:\xa3\x96\xea&\xef\x1cR\x81\xb5\x95\x98\xa0]\xee\x10\x1b\xc23\xf0\xb4\xe3nB;N\x8f6\xe7w\xb2Q\xc5%\xe3)|\xad\x1b\xa2\x08\xe6\xc3\xf8\t<\xefi\\\xcfb\x110r\xf3\x14\x02\x8e\x15"\x13\xc0\xb0\xeb_r\x1c' decrypted = decryptor.decrypt(ciphertext)
3.1.5 改进与代价 该方案核心漏洞是“单符号密文索引 $ B_i $ 不依赖明文”。改进的关键是让算法的行为与明文绑定,破坏这种独立性。有以下几种改进思路:
给随机置换增加明文依赖:原来的字典置换参数($ c_1,\ c_2,\ r_1,\ r_2 $)由流密码生成,与明文无关。改进方法是将这些参数与最后添加的字典条目的哈希值异或,这样置换参数会随之前编码的明文变化。
给随机插入增加明文依赖:原来的新条目插入位置由哈希函数随机选择,hash 函数输入是新字符串,与前向明文无关。改进方法将哈希函数的输入改为“新字符串 + 上一个字典条目的哈希值”,使新条目的插入位置依赖之前编码过的明文。
引入会话初始向量:明文前几个字符没有“之前编码的明文”,完全依赖初始字典,容易泄露。可以在编码前加入一个随机生成的会话初始向量 IV(如 16 字节),并在解密端共享。压缩编码从 IV 开始,使前几个操作依赖不可预测的随机数据,从而增强前缀安全性。
那么代价是什么呢?这些改进会带来两个问题:
计算量增加:需要额外计算哈希值、异或操作,增加了加密和解密的时间;
编码效率进一步降低:IV 的加入会增加额外的编码数据,虽然不影响内容,但会略微降低压缩比。
3.2 随机字典表 该方法建立多个有相同条目但条目顺序不同的字典,每次压缩时随机选择其中一个字典进行最长匹配,并输出索引。由于相同的字符串在不同字典中的位置不同,只有知道每一步使用的是哪个字典,才能正确解码。这种方法称为 RDT(Randomized Dictionary Table)算法。
3.2.1 算法流程 为了实现这一点,Xie[8] 等人于 2005 年在 LZ78 算法的基础上,提出基于一种具有不同入口序的多字典表编码方法,算法生成一个伪随机字典选择序列作为密钥,该序列由伪随机位生成器(PRBG)生成,仅需一个短小的种子即可驱动。整个过程类似流式加密,但密钥流不是用于异或操作,而是用于控制字典选择。字典的初始化和更新策略大致思路是对字典初始条目进行随机置乱,使用密钥控制置乱过程。新条目插入到随机位置,同时将原位置的条目移至当前字典的末尾,当字典满时,这就等同于用新条目替换字典中的一个随机条目。具体步骤如下:
选择一个具有加密效果的安全 PRBG,产生一个 $ r $ 位的种子 $ s $ 作为 RDT 的密钥,并利用 $ s $ 产生密钥流 $ z $。以下所有随机数的生成都由 PRBG 完成。
建立$ E $个具有不同元素顺序的初始化字典,编号依次为 $ 0 $ 至 $ E – 1 $。字典中初始元素顺序是经过随机置乱后的结果,置乱过程根据 $ z $ 采用特定的算法来实现。
生成一个随机数 $ 0 \le d \lt E $,用于从多个字典中随机选取一个进行 LZ78 编码步骤。与 LZW 不同,LZ78 在编码时次输出的是一个二元组 (prefix_index, character),其中 prefix_index 表示当前最长匹配前缀在字典中的编号(若无前缀则为 0),character 是跟在前缀后的新字符。
按如下步骤将新字符串添加到字典表中:
将 $ E $ 个字典平均分成两组(每组包含一半字典)。具体做法为先计算所有可能的分法数量,由于分组不区分顺序,总的有效分法数为:$ \frac{1}{2} \cdot C(E, \frac{E}{2}) $,然后生成一个随机数 $ 0 \le c \lt \frac{1}{2}\ C(E, \frac{E}{2}) $,这个数字 c 对应一种具体的分组方式,用于将字典随机划分为两半。
在 $ 0 \sim N-1 $ 范围内生成两个随机数 $ r_1 $ 和 $ r_2 $($ N $ 为当前字典大小)。
将新字符串插入到前半组所有字典的 $ r_1 $ 位置处,同时将其插入到后半组所有字典的 $ r_2 $ 位置处。并将目标位置的字符串的索引修改为当前字典大小(包含索引 0)的值。
重复步骤 c-d,直到编码完成。
3.2.2 代码实现 这里仅给出 python 的实现,仅作参考。伪随机数生成器使用 RC4 算法;初始字典置乱算法使用 RC4 + Fisher-Yates 算法。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 import structimport timefrom typing import Union , List , Tuple , Optional , Iterablefrom itertools import combinationsclass RC4PRGA : def __init__ (self, key: Union [bytes , str ] ): """ 初始化 RC4 伪随机生成器(PRGA),支持字符串或字节串作为密钥 :param key: RC4 密钥,长度不超过 256 字节 """ self ._original_key = key self .seed(key) def seed (self, key: Union [bytes , str ] ): """ 重置或设置新的密钥,并初始化状态向量 S、指针 i, j :param key: 新的 RC4 密钥 """ if isinstance (key, str ): key = key.encode() if len (key) > 256 : raise ValueError("RC4 密钥不应超过 256 字节" ) self .key = key self .S = self ._ksa() self .i = self .j = 0 def _ksa (self ) -> List [int ]: """ Key-Scheduling Algorithm (KSA):使用密钥初始化 256 字节的状态向量 S :return: 初始化好的 S 列表 """ S = list (range (256 )) j = 0 key_len = len (self .key) for i in range (256 ): j = (j + S[i] + self .key[i % key_len]) & 0xFF S[i], S[j] = S[j], S[i] return S def _prga (self, length: int ) -> bytes : """ Pseudo-Random Generation Algorithm (PRGA):生成指定长度的密钥流段 :param length: 请求的字节数 :return: 密钥流字节序列 """ output = bytearray () for _ in range (length): self .i = (self .i + 1 ) & 0xFF self .j = (self .j + self .S[self .i]) & 0xFF self .S[self .i], self .S[self .j] = self .S[self .j], self .S[self .i] t = (self .S[self .i] + self .S[self .j]) & 0xFF output.append(self .S[t]) return bytes (output) def generate_key_stream (self, length: int ) -> bytes : """ 对外接口:生成指定长度的 RC4 密钥流 :param length: 密钥流长度,必须大于 0 :return: 密钥流(bytes) """ if length <= 0 : raise ValueError("密钥流长度必须大于0" ) return self ._prga(length) def random_int (self, min_val: int , max_val: int ) -> int : """ 生成 [min_val, max_val] 范围内的伪随机整数 :param min_val: 最小值(包含) :param max_val: 最大值(包含) :return: 随机整数 """ if min_val > max_val: raise ValueError("min_val 不能大于 max_val" ) span = max_val - min_val + 1 byte_len = (span.bit_length() + 7 ) // 8 while True : val = int .from_bytes(self ._prga(byte_len), 'big' ) if val < span * (256 ** byte_len // span): return min_val + (val % span) def random_bytes (self, length: int ) -> bytes : """ 生成指定长度的伪随机字节串 :param length: 字节长度,必须大于 0 :return: 随机字节串 """ if length <= 0 : raise ValueError("长度必须大于0" ) return self ._prga(length) def random_hex (self, length: int ) -> str : """ 生成指定长度的伪随机十六进制字符串 :param length: 字符长度(每 2 个字符对应 1 字节) :return: 十六进制字符串 """ if length <= 0 : raise ValueError("长度必须大于0" ) return self ._prga((length + 1 ) // 2 ).hex ()[:length] def sample (self, population: Iterable[int ], k: int ) -> List [int ]: """ 从可迭代整数序列中随机抽取 k 个不重复样本 :param population: 整数序列 :param k: 抽样数量 :return: 长度为 k 的随机样本列表 """ seq = list (population) n = len (seq) if not (0 <= k <= n): raise ValueError("k 必须在 0 到 population 大小之间" ) for i in range (n - 1 , n - k - 1 , -1 ): j = self .random_int(0 , i) seq[i], seq[j] = seq[j], seq[i] return seq[n - k:] class MultiDictLZ78 : def __init__ (self, key: str = '65691f00-5474-4e16-8256-2e2dc711e67d' , E: int = 4 , r: int = 128 , N: int = 10 ): """ 多字典安全 LZ78 压缩器 :param key: 用于初始化 RC4PRGA 的密钥 :param E: 并行字典数量 :param r: 随机种子流比特长度 :param N: 字典地址位宽,最大字典项数 = 2^N """ self .E = E self .dict_size = 1 << N self .prng = RC4PRGA(key) self .seed_key = self .prng.generate_key_stream(r // 8 ) self ._precompute_groupings() def _initialize_dictionaries (self ) -> dict : """ 以同一种子重置所有 E 个字典,并将 0-255 字节随机分布到字典中 :return: 字典 ID 到字节列表的映射 """ self .prng.seed(self .seed_key) dicts = {} byte_vals = [bytes ([i]) for i in range (256 )] for d_id in range (self .E): arr = [None ] * self .dict_size indices = self .prng.sample(range (1 , 255 ), 254 ) for idx, b in zip (indices, byte_vals): arr[idx] = b dicts[d_id] = arr return dicts def _precompute_groupings (self ): """ 生成所有字典分组对(大小 E/2),保证 a<b 排序并去重 """ self .groupings = [] seen = set () for combo in combinations(range (self .E), self .E // 2 ): a = tuple (sorted (combo)) b = tuple (sorted (set (range (self .E)) - set (combo))) if a < b and (a, b) not in seen: self .groupings.append((a, b)) seen |= {(a, b), (b, a)} def _insert_sequence (self, seq: bytes ): """ 将新序列插入到所有字典:选择一组 a/b,生成随机位置 r1,r2, 在组 a 使用 r1,在组 b 使用 r2,并用当前末尾保留旧值 """ a, b = self .groupings[self .prng.random_int(0 , len (self .groupings) - 1 )] cur_len = sum (v is not None for v in self .dicts[0 ]) + 1 r1 = self .prng.random_int(1 , cur_len - 1 ) r2 = self .prng.random_int(1 , cur_len - 1 ) for gid in a: if cur_len < self .dict_size: self .dicts[gid][cur_len] = self .dicts[gid][r1] self .dicts[gid][r1] = seq for gid in b: if cur_len < self .dict_size: self .dicts[gid][cur_len] = self .dicts[gid][r2] self .dicts[gid][r2] = seq def compress (self, data: bytes ) -> bytes : """ 执行压缩并返回打包后的字节流 """ self .dicts = self ._initialize_dictionaries() prefix = b"" output: List [Tuple [int , bytes ]] = [] d_id = self .prng.random_int(0 , self .E - 1 ) dict_cur = self .dicts[d_id] for byte in data: token = prefix + bytes ([byte]) if token in dict_cur: prefix = token else : idx = dict_cur.index(prefix) if prefix in dict_cur else 0 output.append((idx, bytes ([byte]))) self ._insert_sequence(token) d_id = self .prng.random_int(0 , self .E - 1 ) dict_cur = self .dicts[d_id] prefix = b"" if prefix: output.append((dict_cur.index(prefix), b"" )) return self ._pack_bits(output) def decompress (self, bitstream: bytes ) -> bytes : """ 将 compress 打包的字节流还原为原始数据 """ codes = self ._unpack_bits(bitstream) self .dicts = self ._initialize_dictionaries() result = bytearray () d_id = self .prng.random_int(0 , self .E - 1 ) for idx, suf in codes: pref = self .dicts[d_id][idx] or b"" seq = pref + suf result += seq self ._insert_sequence(seq) d_id = self .prng.random_int(0 , self .E - 1 ) return bytes (result) def compress_file (self, file_path: str ) -> str : """ 压缩指定文件,生成 .lzw 后缀的压缩文件 :param file_path: 原文件路径 :return: 压缩后文件路径 (.lzw) """ with open (file_path, 'rb' ) as f: data = f.read() packed = self .compress(data) out_path = file_path + '.lzw' with open (out_path, 'wb' ) as f: f.write(packed) print (f"压缩完成: {out_path} , 原始 {len (data)} B -> 压缩 {len (packed)} B" ) return out_path def decompress_file (self, file_path: str ) -> str : """ 解压 .lzw 文件,生成 .dec 后缀的解压文件 :param file_path: 压缩文件路径 (.lzw) :return: 解压后文件路径 (.dec) """ with open (file_path, 'rb' ) as f: packed = f.read() data = self .decompress(packed) out_path = file_path + '.dec' with open (out_path, 'wb' ) as f: f.write(data) print (f"解压完成: {out_path} , 大小 {len (data)} B" ) return out_path def _pack_bits (self, pairs: List [Tuple [int , bytes ]] ) -> bytes : """ 将 (索引, 后缀) 对打包成二进制流: 1B 长度 L + 4B 大端索引 + LB 后缀 """ buf = bytearray () for count, val in pairs: if not 0 <= len (val) < 256 : raise ValueError("val 长度必须在 0-255 之间" ) buf += struct.pack('>B' , len (val)) buf += struct.pack('>I' , count) buf += val return bytes (buf) def _unpack_bits (self, stream: bytes ) -> List [Tuple [int , bytes ]]: """ 按 _pack_bits 格式逐条解析打包数据 """ res: List [Tuple [int , bytes ]] = [] offset = 0 total = len (stream) while offset + 5 <= total: L = stream[offset] count = struct.unpack('>I' , stream[offset+1 :offset+5 ])[0 ] offset += 5 if offset + L > total: raise ValueError("val 长度超出剩余字节" ) val = stream[offset:offset+L] offset += L res.append((count, val)) return res if __name__ == "__main__" : seed = '65691f00-5474-4e16-8256-2e2dc711e67d' lz78 = MultiDictLZ78(key=seed, E=4 ) plaintext = b'ABABABAABAAABAAAABABABABABBBABABBABABBABBABABABBBBABABABAAAABABABAABABAABABBABABABBAABBABABABABABABABBABABABABABABABABABABABABABABABABABABABABABABABABABBA' compressed = lz78.compress(plaintext) print (f"压缩编码: {compressed} " ) print (f"原始长度: {len (plaintext)} -> 压缩长度: {len (compressed)} \n" ) decompressed = lz78.decompress(compressed) print (f"解压结果: {decompressed} " ) print (f"加解密一致性: {decompressed == plaintext} " )
3.2.3 攻击方案 Xie 的方案同样存在可被单字符攻击利用的漏洞。由于每次编码输出前缀索引后,字典的随机选择仅由密钥决定,与明文无关,因此单字符在每次随机选择后的字典中的位置是相对固定的。攻击者可以遍历 n 步随机字典选择路径,构建单字符前缀的查找表,从而还原出部分明文信息,造成信息泄露。
攻击脚本(Python):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 import jsonimport stringimport structfrom pathlib import Pathfrom typing import Any , Dict , List , Optional , Tuple from concurrent.futures import ProcessPoolExecutorfrom tqdm import tqdmfrom Xie_LZW import MultiDictLZ78class XieLZ78CPA : BITS_PER_CODE = 10 PAD_CHAR_RANGE = [chr (i) for i in range (32 , 127 )] CHARACTER_TABLE = string.ascii_letters + string.digits + " ,.{}\"\'-!" def __init__ (self, lut_path: Path, lzw_instance: Any , regenerate_lut: bool = False , pad_range: range = range (0 , 200 ): """ 初始化 ZhouLZWCPA 解密器 :param lut_path: 查找表路径(JSON) :param lzw_instance: 支持 compress 方法的 LZW 实例 :param regenerate_lut: 是否强制重建查找表 :param pad_range: 查找表构建时使用的填充步长范围 """ self .lut_path = lut_path self .lzw = lzw_instance self .regenerate_lut = regenerate_lut self .combinations = [a + b for a in XieLZ78CPA.PAD_CHAR_RANGE for b in XieLZ78CPA.PAD_CHAR_RANGE] self .pad_range = pad_range self .lut: Dict [str , Dict [str , str ]] = {} @staticmethod def _unpack_bits (stream: bytes ) -> List [Tuple [int , bytes ]]: """ 按 _pack_bits 格式逐条解析打包数据 """ res: List [Tuple [int , bytes ]] = [] offset = 0 total = len (stream) while offset + 5 <= total: L = stream[offset] count = struct.unpack('>I' , stream[offset + 1 :offset + 5 ])[0 ] offset += 5 if offset + L > total: raise ValueError("val 长度超出剩余字节" ) val = stream[offset:offset + L] offset += L res.append((count, val)) return res def _generate_padded_input (self, char: str , pad_count: int ) -> str : """ 生成指定字符的填充明文字节串 :param char: 明文字节 :param pad_count: 参与填充的字符组数 :return: 带填充的明文字节串 """ return '' .join(self .combinations[:pad_count]) + char def _generate_plaintexts (self, pad: int ) -> List [str ]: """ 构造当前 pad 值对应的所有测试明文列表 """ return [self ._generate_padded_input(ch, pad) for ch in XieLZ78CPA.CHARACTER_TABLE] def _build_single_lut (self, pad: int ) -> Dict [Tuple , str ]: """ 构建特定填充步长 pad 下的查找表 :param pad: 当前步长 :return: 查找表 {index: character} """ lut = {} for plaintext in tqdm(self ._generate_plaintexts(pad), desc=f"构建查找表步长: {pad} " ): try : encoded = self .lzw.compress(plaintext.encode()) index_list = self ._unpack_bits(encoded) lut[index_list[pad]] = plaintext[-1 ] except Exception: continue return lut def _load_or_generate_lut (self ) -> bool : """ 加载或生成所有步长的查找表 :return: 是否成功 """ if self .regenerate_lut or not self .lut_path.exists(): try : print ("开始构建查找表..." ) with ProcessPoolExecutor() as executor: results = list (executor.map (self ._build_single_lut, self .pad_range)) self .lut = {str (p): {str (k[0 ]): v for k, v in d.items()} for p, d in zip (self .pad_range, results)} with open (self .lut_path, 'w' ) as f: json.dump(self .lut, f, ensure_ascii=False , indent=2 ) print (f"查找表保存成功: {self.lut_path} " ) return True except Exception as e: print (f"查找表构建失败: {e} " ) return False else : try : with open (self .lut_path, 'r' ) as f: self .lut = json.load(f) print (f"成功加载查找表: {self.lut_path} " ) return True except Exception as e: print (f"查找表加载失败: {e} " ) return False def decrypt (self, ciphertext: bytes ) -> Optional [str ]: """ 使用查找表对密文进行解码 :param ciphertext: 密文字节流(经过 LZW 压缩) :return: 解密后的明文字符串或 None """ if not self ._load_or_generate_lut(): return None try : print ("\n开始解密..." ) decrypted = [] indices = self ._unpack_bits(ciphertext) print (indices) for step, idx in enumerate (indices): char = self .lut.get(str (step), {}).get(str (idx[0 ]), '*' ) decrypted.append(char + idx[1 ].decode()) print (f"步骤 {step:02d} : 索引 {idx[0 ]:04d} -> 明文 '{char} '" ) result = '' .join(decrypted) print ("\n最终解密结果:" , result) return result except Exception as e: print (f"解密失败: {e} " ) return None if __name__ == "__main__" : lut_path = Path("lut.json" ) lzw = MultiDictLZ78() decryptor = XieLZ78CPA( lut_path=lut_path, lzw_instance=lzw, regenerate_lut=True , pad_range=range (0 , 200 ) ) ciphertext = b'\x01\x00\x00\x00\x08a\x01\x00\x00\x00\xc8t\x01\x00\x00\x00rs\x01\x00\x00\x00\xd3"\x01\x00\x00\x00\xd8s\x01\x00\x00\x00\xeei\x01\x00\x00\x00f \x01\x00\x00\x00\xb0h\x01\x00\x00\x00\x81 \x01\x00\x00\x00Hh\x01\x00\x00\x00\x9dp\x01\x00\x00\x01\x06w\x01\x00\x00\x007e\x01\x00\x00\x008,\x01\x00\x00\x00\x0bt\x01\x00\x00\x00\xb9r\x01\x00\x00\x00\xc8i\x01\x00\x00\x00\xc8g\x01\x00\x00\x00\x1do\x01\x00\x00\x00\x12a\x01\x00\x00\x00Hd\x01\x00\x00\x00H \x01\x00\x00\x00ke\x01\x00\x00\x00\xcay\x01\x00\x00\x01\x06u\x01\x00\x00\x00\' \x01\x00\x00\x00\\a\x01\x00\x00\x007,\x01\x00\x00\x00\xd9c\x01\x00\x00\x00\x18m\x01\x00\x00\x00\x95t\x01\x00\x00\x00\ni\x01\x00\x00\x00\xc9w\x01\x00\x00\x00\xe0y\x01\x00\x00\x00\r \x01\x00\x00\x00_I\x01\x00\x00\x00\xc8 \x01\x00\x00\x00\xab \x01\x00\x00\x00\xd5o\x01\x00\x00\x00\xd5e\x01\x00\x00\x00\x9b,\x01\x00\x00\x00\xcbi\x01\x00\x00\x00\xae"\x01\x00\x00\x00\xd8a\x01\x00\x00\x00\xfes\x01\x00\x00\x00\x89e\x01\x00\x00\x00/e\x01\x00\x00\x00VD\x01\x00\x00\x00\xeen\x01\x00\x00\x00\x91e\x01\x00\x00\x01+,\x01\x00\x00\x00\xca"\x01\x00\x00\x00\xcdd\x01\x00\x00\x00\x8bI\x01\x00\x00\x00\xd5 \x01\x00\x00\x01\x00i\x01\x00\x00\x00\xaf \x01\x00\x00\x01&o\x01\x00\x00\x01\x14.\x01\x00\x00\x00_T\x01\x00\x00\x00\xe7e\x01\x00\x00\x00\xd3c\x01\x00\x00\x00\xabl\x01\x00\x00\x00\xb6i\x01\x00\x00\x00\x8dt\x01\x00\x00\x00\x1a \x01\x00\x00\x00\xc3 \x01\x00\x00\x00Pr\x01\x00\x00\x01\x07w\x01\x00\x00\x01% \x01\x00\x00\x00\x0e \x01\x00\x00\x01\x11a\x01\x00\x00\x01\'d\x01\x00\x00\x00\xd8-\x01\x00\x00\x00\xf5 \x01\x00\x00\x00_L\x01\x00\x00\x01\x07t\x01\x00\x00\x01Cg\x01\x00\x00\x00\x18!\x01\x00\x00\x00r \x01\x00\x00\x00\xe0h\x01\x00\x00\x00\x95a\x01\x00\x00\x00\xfec\x01\x00\x00\x00\xd5o\x01\x00\x00\x01\x06 \x01\x00\x00\x01>s\x01\x00\x00\x01Ci\x01\x00\x00\x01?t\x01\x00\x00\x00\xcdt\x01\x00\x00\x01My\x01\x00\x00\x00\xd8d\x01\x00\x00\x00/o\x01\x00\x00\x00\xd1p\x01\x00\x00\x00\x81d\x01\x00\x00\x00\x1ba\x01\x00\x00\x007d\x01\x00\x00\x01Lh\x01\x00\x00\x00\x95c\x01\x00\x00\x01Ua\x01\x00\x00\x01\x1bn\x01\x00\x00\x00\xd8r\x01\x00\x00\x00\x02 \x01\x00\x00\x01\x06a\x01\x00\x00\x00\x80t\x01\x00\x00\x00$n\x01\x00\x00\x00Pt\x01\x00\x00\x005r\x01\x00\x00\x00\xa5g\x01\x00\x00\x01U \x01\x00\x00\x01Op\x01\x00\x00\x00\x18r\x01\x00\x00\x00\xd2-\x01\x00\x00\x00\x8el\x01\x00\x00\x00r.\x01\x00\x00\x00\xcaD\x01\x00\x00\x01Xe\x01\x00\x00\x00\xc9c\x01\x00\x00\x01\x1cn\x01\x00\x00\x00\x80i\x01\x00\x00\x007u\x01\x00\x00\x00" \x01\x00\x00\x00\xabt\x01\x00\x00\x00\xd8h\x01\x00\x00\x01\x1es\x01\x00\x00\x00\x0bp\x01\x00\x00\x00\x1as\x01\x00\x00\x00\x80 \x01\x00\x00\x015 \x01\x00\x00\x009p\x01\x00\x00\x01\'t\x01\x00\x00\x00ro\x01\x00\x00\x01@ \x01\x00\x00\x01Zr\x01\x00\x00\x005e\x01\x00\x00\x01%e\x01\x00\x00\x00\xd8o\x01\x00\x00\x00\xd2t\x01\x00\x00\x00op\x01\x00\x00\x01jl\x01\x00\x00\x00\x1at\x01\x00\x00\x00\xafu\x01\x00\x00\x00\x9bi\x01\x00\x00\x01M \x01\x00\x00\x010i\x01\x00\x00\x01Cm\x01\x00\x00\x00\xcdo\x01\x00\x00\x00ru\x01\x00\x00\x00wr\x01\x00\x00\x01Yw\x01\x00\x00\x00\xees\x01\x00\x00\x00\xbeo\x01\x00\x00\x00\xd5p\x01\x00\x00\x00\xd9e\x01\x00\x00\x01\x11d\x01\x00\x00\x00\xd0n\x01\x00\x00\x01vt\x01\x00\x00\x00mn\x01\x00\x00\x00\xdbe\x01\x00\x00\x00_d\x01\x00\x00\x00\xace\x01\x00\x00\x01\x89,\x01\x00\x00\x01\x08H\x01\x00\x00\x00\xe4f\x01\x00\x00\x00>m\x01\x00\x00\x00it\x01\x00\x00\x00%e\x01\x00\x00\x00\xd8c\x01\x00\x00\x00\x18l\x01\x00\x00\x00Ks\x01\x00\x00\x01\x8bd\x01\x00\x00\x01\x98q\x01\x00\x00\x01`a\x01\x00\x00\x010 \x01\x00\x00\x01\x7fy\x01\x00\x00\x00\xabr\x01\x00\x00\x00\xacs\x00\x00\x00\x00\r' decrypted = decryptor.decrypt(ciphertext)
3.3 其他方案 除了前述方法,LZW 的联合压缩加密还有许多其他研究。例如,Hermassi[11] 等人利用混沌映射生成密钥流,动态更新 Huffman 树,使得同一符号可以对应多个等长但不同的编码,提高了安全性;Liu[12] 等人则提出了一种改进的 Huffman 树突变机制,通过仅修改内结点,避免了每次突变后对整棵树重新编码的开销。
由于篇幅有限,这里不再逐一展开。如果有小伙伴对方法感兴趣,后续我会专门写一篇文章进行深入讲解。
4. 总结 目前 LZW 算法的研究主要集中在两个方向:
一是压缩性能的优化。现有很多改进方案要么压缩速度快但压缩率低,要么压缩率有所提升但处理速度下降,很难两者兼顾。
二是压缩与加密的结合。目前的联合加密方案也普遍存在效率与安全难以兼顾的问题,比如:
使用软件生成的伪随机数种子并存储在非易失性存储器(NVM)中,容易被攻击者窃取;
多字典方案虽然增加了安全性,但占用大量内存;
使用复杂数学模型打乱条目顺序会显著增加计算负担。
如何在保证安全的前提下,实现高效压缩,仍是 LZW 研究中的一个重要难题。
参考 参考资料:
Wiki: Lempel–Ziv–Welch
LZW压缩算法原理解析
可能是最通俗的Lempel-Ziv-Welch (LZW)无损压缩算法详述
庖丁解牛:GIF
你真的了解 gif 吗?分析 gif 文件和一些奇怪的 gif 特性
深入浅出 GIF
GIF Codec – LZW Compression Algorithm 12月 20 2017 LZW算法
参考文献:
[1] 徐秉铮,吴立忠,Victor,等. 中文文本压缩的LZW算法[J]. 华南理工大学学报(自然科学版),1989,17(3): 1-9.
[2] 华强. 中西文文本压缩的LZWCH算法[J]. 计算机工程与应用,1999,(3): 22-23,35.
[3] 陈庆辉,陈小松,韩德良. 中文文本压缩的LZW算法[J]. 计算机工程与应用,2014,(3): 112-116.
[4] 武彦霞. 基于LZW字典压缩算法的改进研究[D]. 江苏科技大学,2024.
[5] 肖志文,陈伟,梁久祯,等. 基于LZW算法的中文文本压缩算法[C]//2007北京地区高校研究生学术交流会通信与信息技术会议. 2008-01.
[6] 王安. 基于LZW压缩算法的数字图像加密研究[D]. 重庆大学,2013.
[7] 成小勇. LZW数据压缩的改进与加密研究[D]. 东南大学,2022.
[8] Dahua Xie, C.-C. Jay Kuo. Secure Lempel-Ziv Compression with Embedded Encryption[J]. Proc. SPIE, 2005, 5681:318-327.
[9] Jiantao Zhou, Oscar C. Au, Xiaopeng Fan and P. Hon-Wah Wong. Secure Lempel-Ziv-Welch (LZW) algorithm with random dictionary insertion and permutation[C] in Proceedings of 2008 IEEE International Conference on Multimedia and Expo (ICME`2008), 2008, 245-248.
[10] Shujun Li, Chengqing Li, J. C.‑C. Kuo. On the security of a secure Lempel–Ziv–Welch (LZW) algorithm[C]//Proc. 2011 IEEE Int. Conf. on Multimedia and Expo (ICME), Barcelona, Spain, 2011: 1–5.
[11] Hermassi H, Rhouma R, Belghith S. Joint compression and encryption using chaotically mutated Huffman trees[J]. Communications in Nonlinear Science & Numerical Simulation, 2010, 15(10): 2987-2999.
[12] Liu Y, Li B, Zhang Y, et al. A Huffman-Based Joint Compression and Encryption Scheme for Secure Data Storage Using Physical Unclonable Functions[J]. Electronics, 2021, 10(11): 1267.

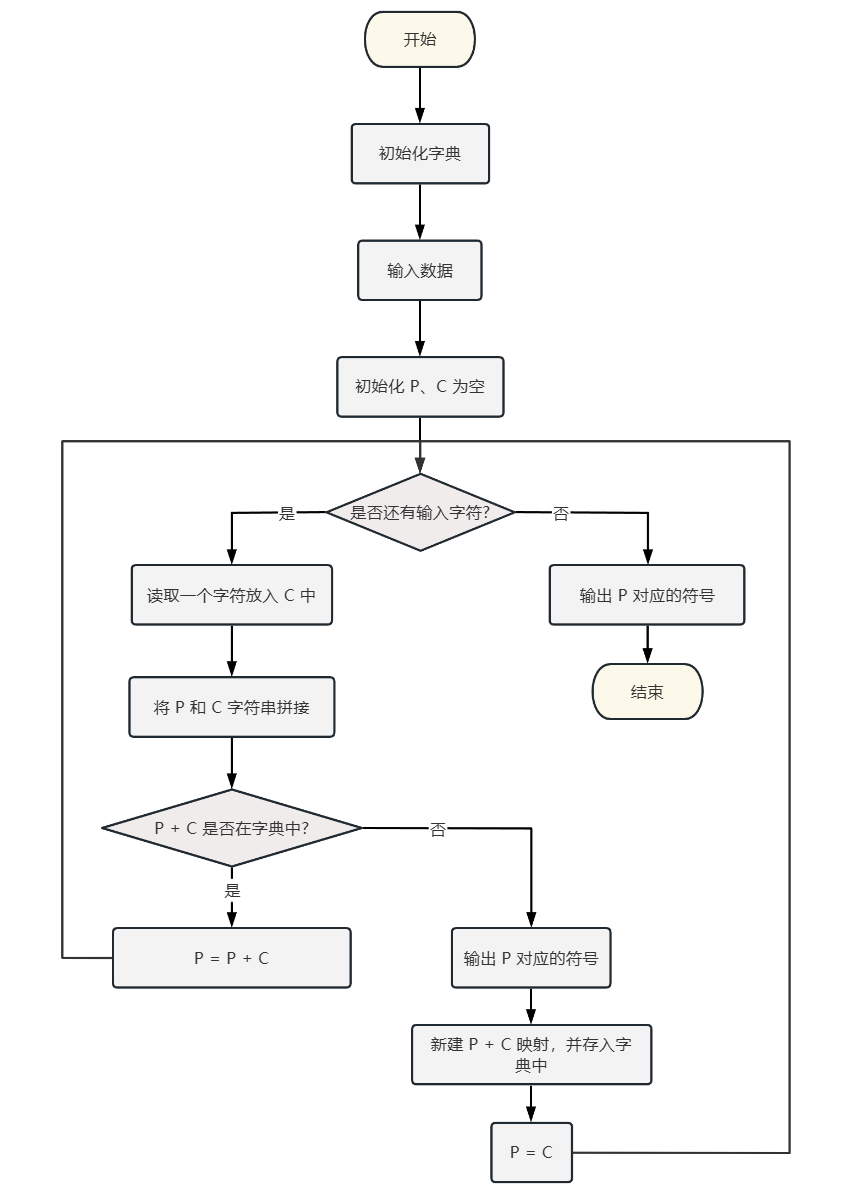

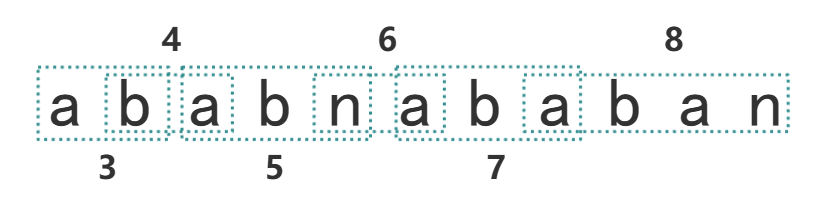

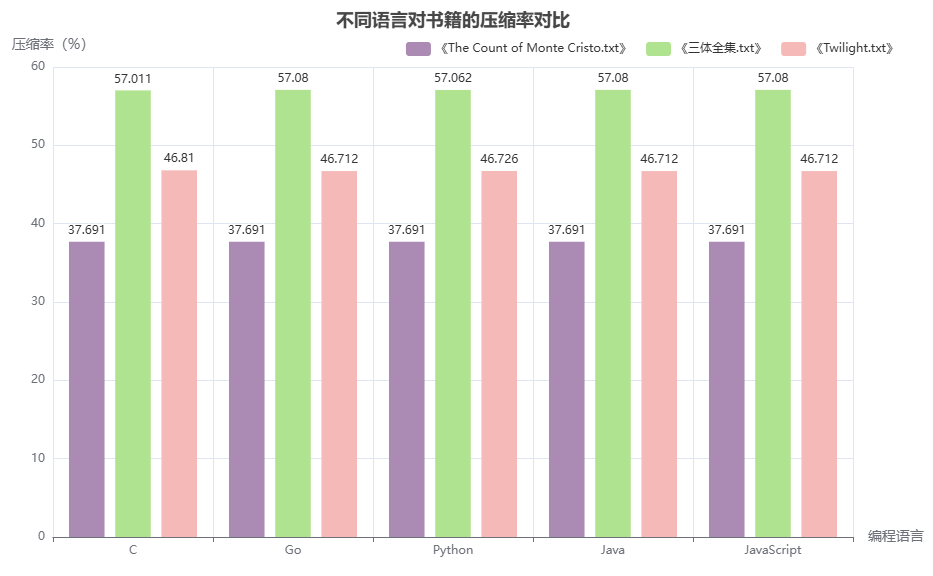
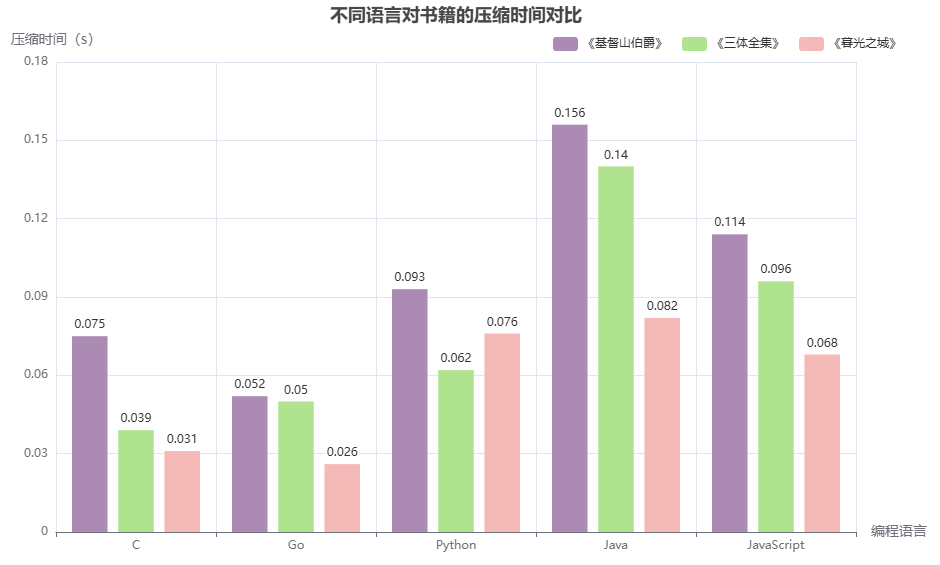
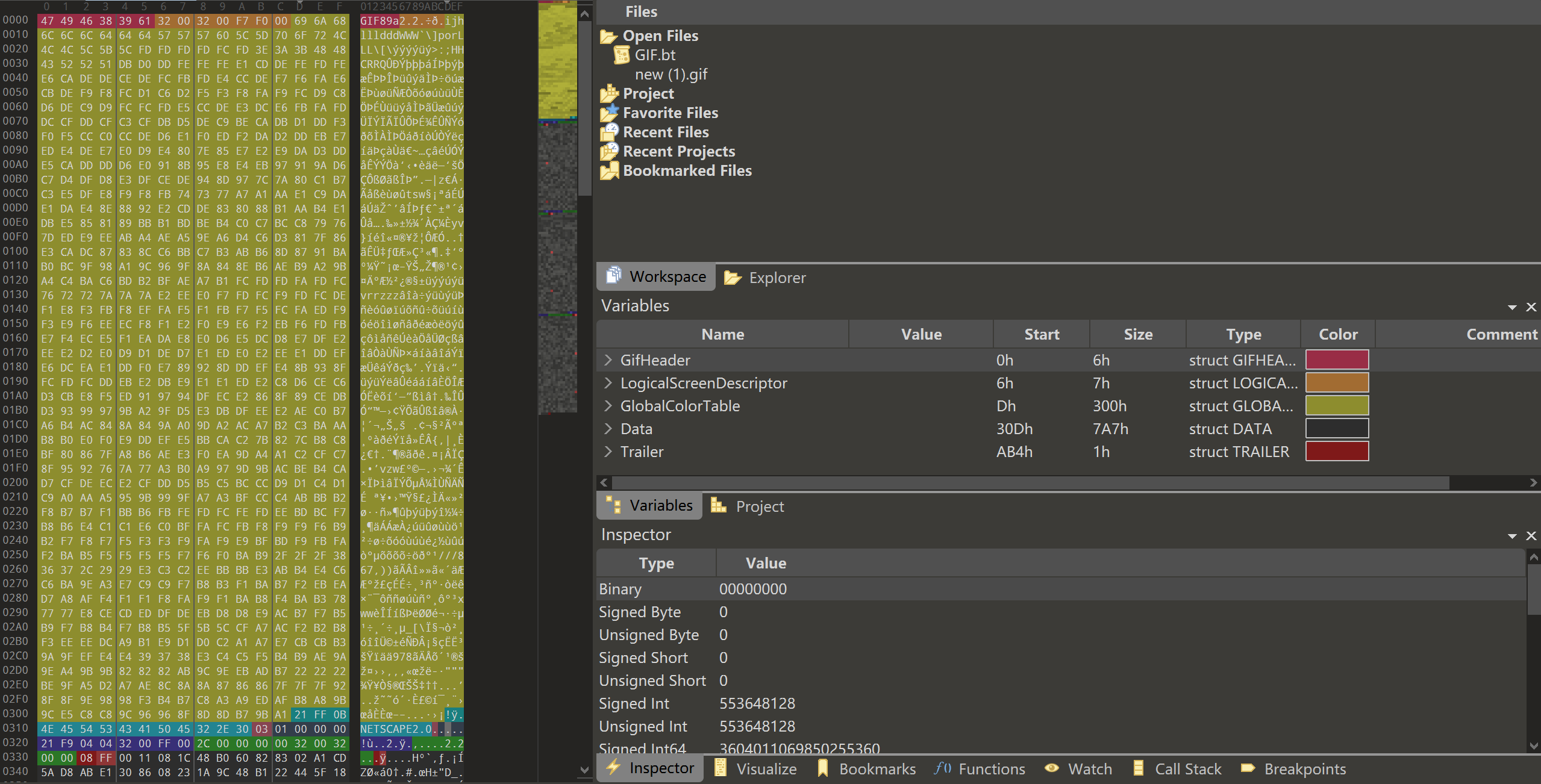
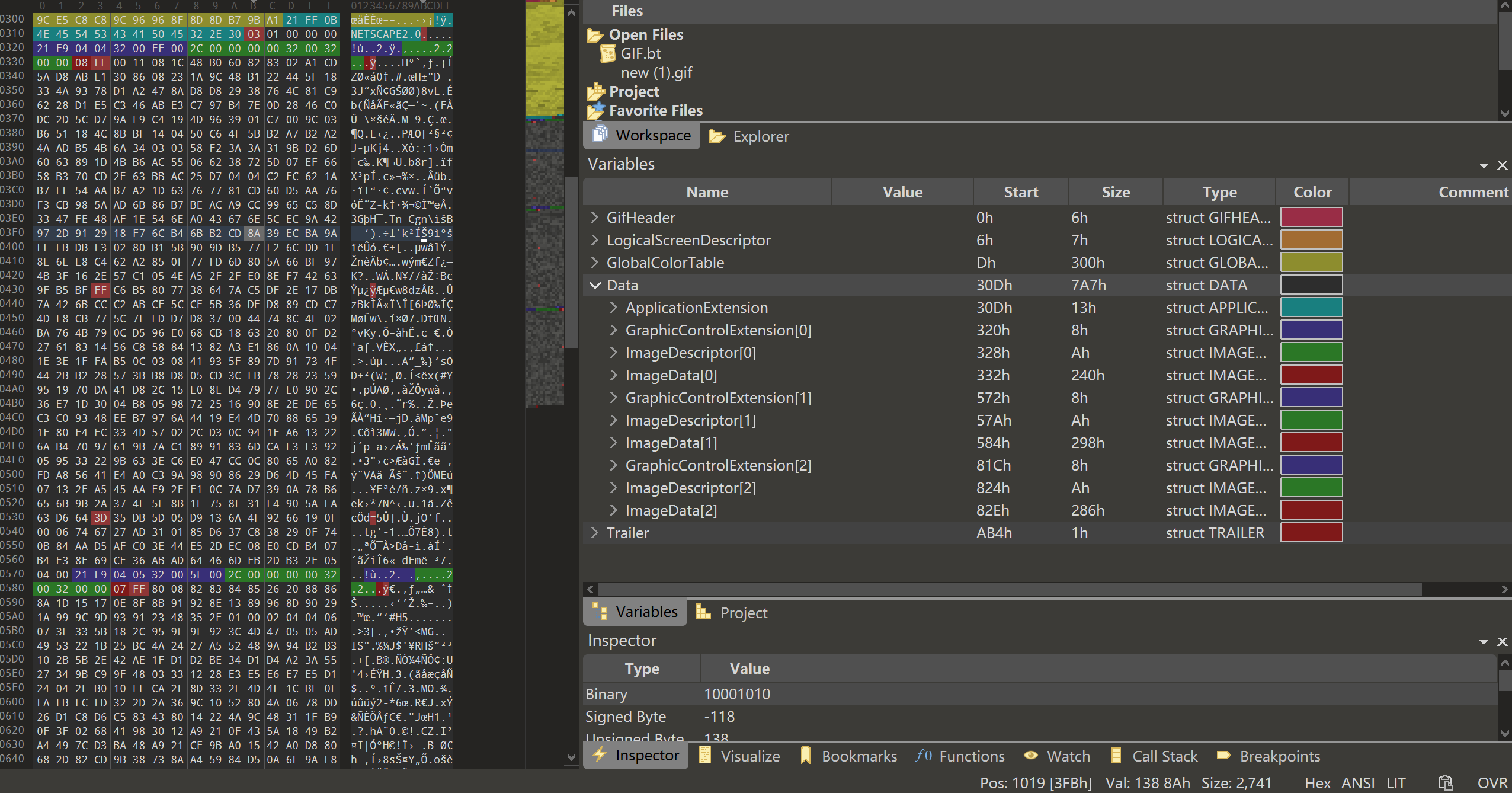
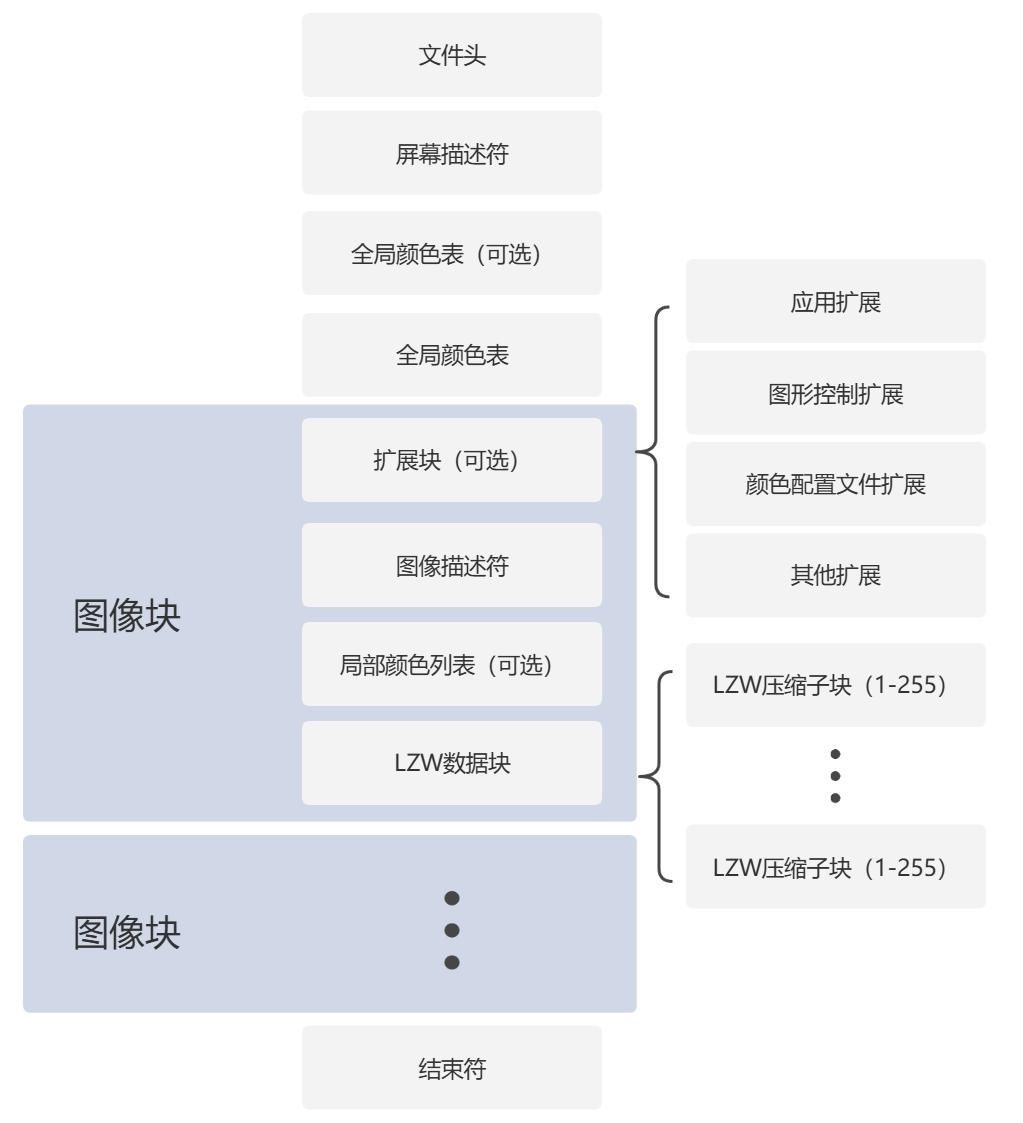
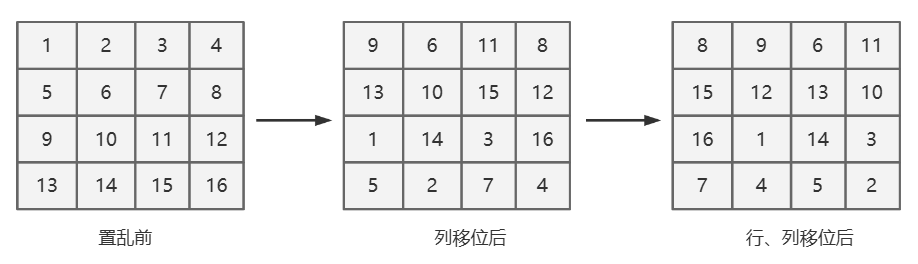
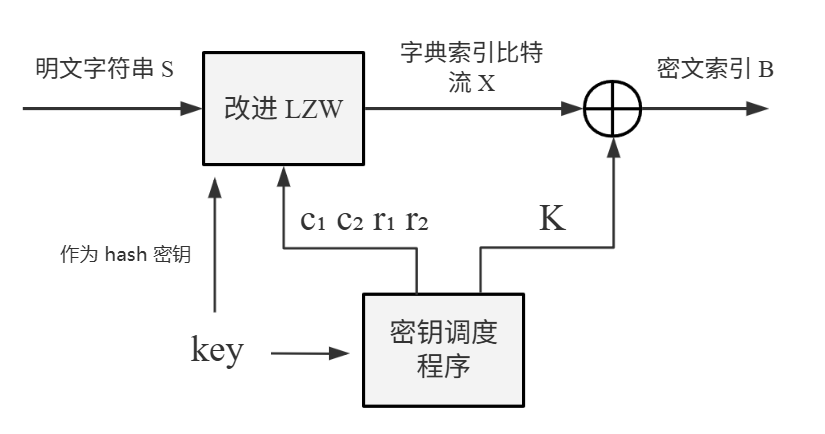



![[古典密码] 单表替换密码](https://dstbp.com/data/imgs/posts/msc/Thumbnail.png)
![[古典密码] 隐写式单表替换密码](https://dstbp.com/data/imgs/posts/smsc/Thumbnail.png)
![[信息编码] LZW 压缩算法](https://dstbp.com/data/imgs/posts/lzw/Thumbnail.png)
![[日常训练] Crypto Training - BUUCTF(一)](https://dstbp.com/data/imgs/posts/buuctf/Thumbnail.png)